45+ [REAL-TIME] NumPy Interview Questions And Answers

NumPy is a crucial library for numerical computing in Python, designed to handle large, multi-dimensional arrays and matrices. It includes a variety of mathematical functions that enable efficient operations on these arrays, making it indispensable for data analysis, scientific computing, and machine learning. Its performance efficiency and seamless compatibility with other libraries make NumPy a vital resource for data-centric projects.

1. What is NumPy, and how is it different from Python lists?

Ans:

NumPy stands for Numerical Python. It is a library written purely for numerical computations in the Python language. Elements of a NumPy array must be the same type, unlike aspects of a list in Python. This property ensures more efficient memory usage and faster operations. NumPy is particularly well suited for handling large volumes of data and mathematical calculations.

2. What are the advantages of using NumPy arrays over Python lists?

Ans:

Advantages of NumPy arrays over Python lists: better performance NumPy arrays are implemented in C, which is optimized for speed. They require less memory than Python lists and support vectorized operations. A big library of mathematical functions and methods is also provided with NumPy, which simplifies otherwise complex computations, increasing efficiency and usability.

3. What is a NumPy array, and how is it different from a list? 

Ans:

• A NumPy array is an n-dimensional grid of homogenous-type values indexed by a tuple of nonnegative integers. The primary difference compared with a Python list is that a NumPy array cannot change the size by which it was created once defined. 
• Moreover, the data types are coherent. Since lists can only hold a few types of data and extend their lengths, while NumPy arrays have much richer support for complex math operations and optimize performance, they are intended to be used instead of lists, especially if numerical operations need to be done.

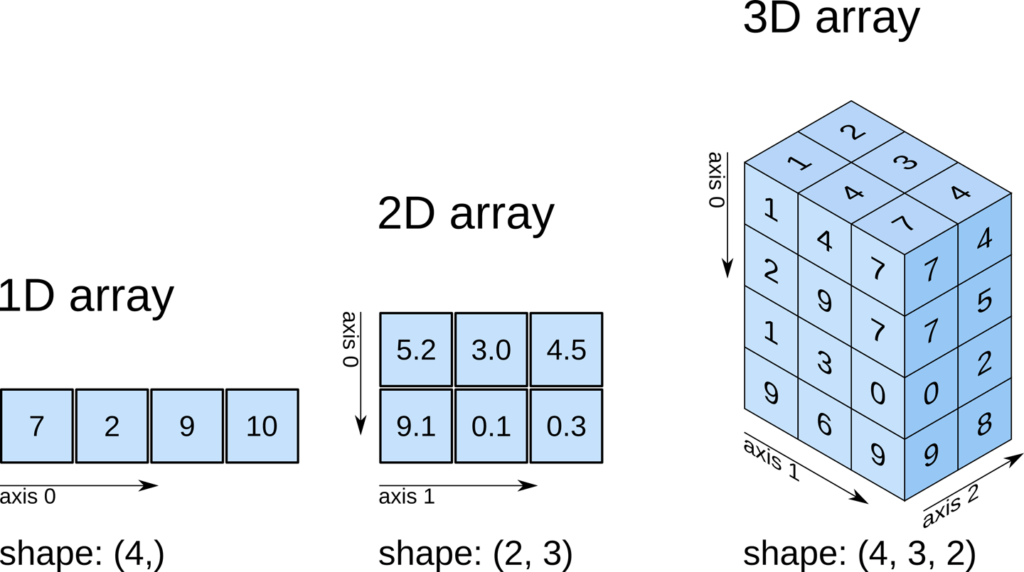
4. What is ‘np.empty()’ used for in NumPy?  

Ans:

• The ‘np. The empty ()’ function creates a new array of a given shape and a specified data type without initializing its contents. 
• If the values are assigned later, it is very handy for performance. Since this function does not initialize the array, initial values are likely unpredictable, reflecting what was in memory before if not handled properly.

5. Explain the difference between ‘np.arange()’ and ‘np.linspace()’. 

Ans:

The ‘np. Arrange ()’ function returns an array of evenly spaced values over a specified range by creating a selected range of values with a defined step size. In other words, with ‘np. linspace()’, one specifies the number of points to return and produces that number of evenly spaced values between two endpoints, independent of the step size. While ‘np. Arrange ()’ is flexible with its step size, and ‘np. linspace()’ is typically better suited to cases where it is important to have a certain number of points.

6. What is the difference between ‘np.array()’ and ‘np.asarray()’?

Ans:

Feature	‘np.array()’	‘np.asarray()’
Purpose	Creates a new array.	Converts input to an array, returning a view if possible.
Copy Behavior	Always creates a copy of the input data.	Only copies data if the input is not already an array.
Input Type	Accepts lists, tuples, or other arrays.	Primarily designed for array-like inputs (e.g., lists, tuples).
Data Type	Can explicitly specify the data type (‘dtype’).	Also allows specifying ‘dtype’, but will return an existing array’s dtype if possible.
Performance	Slightly slower due to copying.	More efficient when no copy is needed.

7. What is fancy indexing in NumPy?  

Ans:

• What is referred to as “fancy indexing” is using arrays of indices instead of simple slices to access and modify elements of an array. 
• It allows element selection out of non-contiguous elements and can nicely rearrange data. 
• For example, an array of indices will return the elements at the corresponding index from the original array.

8. What is broadcasting in NumPy?  

Ans:

• Broadcasting is a mechanism that allows NumPy to perform arithmetic operations between different shapes of arrays. 
• The occurrence of arrays with differing shapes during arithmetic operations triggers NumPy to expand the smaller-dimension array to match the size of the larger-dimension array during such operations. 
• This aspect makes programming easier and more efficient because one does not have to copy data repeatedly.

9. What are the conditions required for broadcasting to occur?

Ans:

Broadcasting occurs only if the arrays have the same number of dimensions or if one has a dimension size of one, allowing it to stretch to match the size of the other array. In addition, dimensions must be compatible in that they should be either the same or one of them equal to 1, ensuring that no duplicate data is returned. This functionality greatly enhances the flexibility and efficiency of operations on arrays in numerical computations.

10. What is vectorization, and why is it important in NumPy? 

Ans:

Vectorizing an operation means applying it to every element in an array simultaneously without explicitly using it for loops. It’s very important for NumPy because it results in much more succinct and readable code yet makes it much faster. Low-level, optimized implementations enable vectorized operations to execute more quickly, so they are great for the sort of large numerical computations that NumPy’s speed advantages serve best for.

11. How does NumPy optimize operations with vectorization?

Ans:

• NumPy optimizes operations through vectorization by executing operations on entire arrays rather than individual elements. 
• This is achieved using underlying C libraries, which significantly speed up computations by reducing the overhead of Python loops. 
• Vectorized operations also leverage the parallel processing capabilities of modern CPUs, making them more efficient for large datasets. 
• Overall, vectorization leads to cleaner and more concise code, enhancing performance in numerical computations.

12. What is the role of np.random.choice()?

Ans:

• The np. random.The choice () function generates random samples from a specified array or range. It provides options for sampling with or without replacement, allowing the same element to be selected multiple times or only once. 
• This function can also incorporate probability weights, enabling certain elements to be chosen more frequently than others. 
• Its versatility makes it ideal for data analysis simulations, statistical modelling, and sampling tasks.

13. What is the difference between np.random.rand() and np.random.randn()? 

Ans:

The np. random.rand() function generates random numbers uniformly distributed between 0 and 1, producing values in a specified shape defined by the user. In contrast, np. Random. Rand () generates random numbers from a standard normal distribution, meaning they have a mean of 0 and a variance of 1. The key distinction lies in their distribution types: rand() is uniform, while rand () is normal, affecting how the random numbers are generated and utilized.

14. What is np.linalg.Norm () used for?

Ans:

The np. linalg.norm() function calculates the norm of a vector or matrix, providing a measure of its length or size. Different types of norms can be computed, including the Euclidean norm (L2 norm) and the Frobenius norm for matrices. This function is widely used in various mathematical and statistical applications, such as optimization and machine learning, to assess distances, magnitudes, and the overall scale of data.

15. What is the difference between np.dot() and np.matmul()?

Ans:

• The np. dot() function computes the dot product of two arrays and can handle both vector and matrix operations. It treats 1D arrays as vectors and returns a scalar result for such inputs. 
• On the other hand, np. Mammal () is specifically designed for matrix multiplication and adheres to the rules of linear algebra. 
• It is more explicit in its operation, making it preferable for scenarios involving higher-dimensional arrays and matrix calculations.

16. What is the difference between shallow and deep copies in NumPy?

Ans:

• In NumPy, a shallow copy refers to creating a new array object that references the same data as the original, meaning changes to either array will affect the other. 
• Conversely, a deep copy creates a new array with an entirely independent copy of the original data, ensuring that modifications do not impact the original array. 
• This distinction is important when working with mutable data, as it helps to avoid unintended side effects in computations.

17. What is the purpose of np. Copy () in NumPy?

Ans:

The np. copy() function creates a deep copy of an array, producing a new array that holds the same data as the original while maintaining independence. This is particularly useful when modifying a variety without altering the original data is necessary by ensuring that changes to the copied array do not affect the source array, np. Copy () helps maintain data integrity and manage memory effectively in various computational tasks.

18. What does the np. New axis function do?

Ans:

The ‘np. The new axis function increases the dimensions of an existing array by one, facilitating more complex array manipulations and broadcasting. Introducing a new axis can transform a 1D array into a 2D array, allowing for alignment in shape for various operations, such as matrix multiplication. This feature enhances the flexibility of handling arrays in NumPy, simplifying the reshaping and rearranging of data. Consequently, it enables more efficient computation and better utilization of array operations in numerical analyses.

19. What is the difference between np. Transpose () and the .T attribute?

Ans:

• Both np. Transpose () and the .T attribute are utilized for transposing arrays, which involve swapping rows and columns. 
• The key difference is that np. Transpose () can accept additional arguments to specify the axes for transposition, allowing for more complex reshaping of multidimensional arrays. 
• In contrast, the .T attribute serves as a shorthand for transposing and is primarily used for 2D arrays, simplifying basic operations.

20. How does NumPy optimize operations with vectorization?

Ans:

• The operations in NumPy use vectorization to optimize computations. This is achieved by using the underlying C libraries for computations to reduce the overhead associated with loops significantly. 
• Vectorized operations apply modern CPUs’ underlying parallel processing capabilities, making these codes much faster for large datasets. 
• Generally, vectorized code is much clearer and terser than code written with loops; thus, it delivers better performance in numeric computations.

21. What does np. Random. choice() do?

Ans:

The function np. Random. Choice () produces a random sample from the given list or within a given range. It also allows with and without replacement options so an element may appear multiple times in the sample or just once. This function can also include weight, so some elements can be more likely to be selected. Hence, it is widely applied for many simulations, statistical modelling, and sampling applications in data analysis.

22. What is the difference between np.random.rand() and np. Random. Rand ()?

Ans:

The np. random.rand() function returns the random numbers uniformly distributed between 0 and 1. The returned values are of a specified shape as defined by the user. Against this, np. Random. Rand () returns numbers from a standard normal distribution whose mean value is 0 and variance is 1. The main difference is that one returns numbers of uniform distribution while the other returns normal distribution, which reflects how the random numbers are generated and used. The np. linalg.norm() function calculates the norm of vectors or matrices, giving an overview of the size of its length.

23. What are the differences between np.dot() and np.matmul()?

Ans:

• The np. dot() operation applies the dot product to two arrays, which may perform vector and matrix operations. 
• For 1D arrays, it acts on those as vectors and returns a scalar result. On the contrary, np. matmul() is designed only for matrix multiplication and adheres strictly to linear algebra. 
• It is more explicit because it demands matrices rather than higher dimensional arrays and matrix calculations.

24. What is a deep and shallow copy of an array in NumPy?

Ans:

• In NumPy, a shallow copy is a copy reference to a new array object that references the original array’s data. So, any modifications to the latest copy also affect the original array and vice versa. 
• Contrasting this, a deep copy creates a new array with a completely independent copy of the original data. Therefore, any change is not at risk of affecting the original array. 
• This is an important feature for dealing with mutable data-it can easily eliminate unwanted side effects in computations.

25. What is np. Copy () in NumPy?

Ans:

Applying the np. Copy () function to an array produces a deep copy of an array entirely independent of the source with the same data. It is useful when it is necessary or desirable to change a variety without affecting the data from which the object was originally derived. As changes to the copied array are not propagated into the source, this provides an efficient method to preserve data integrity and effectively utilize memory with computation applications.

26. What does np. newaxis do?

Ans:

The use of np. The new axis increases by one of the dimensions of an array already in place, making more complex manipulations and broadcasts easier on arrays. It can change a 1D array to a 2D array, making it possible to align shapes for operations of various kinds, such as multiplying a matrix. This increases flexibility in handling arrays in NumPy by making it easier to reshape and rearrange data as needed.

27. What is the difference between np. Transpose () and the .T attribute?

Ans:

• Both np. Transpose () and the .T attribute are used for array transposing or switching the rows and columns. 
• The basic difference is that np. Transpose () has optional arguments specifying the axes to transpose, which allows it to be applied to reshape more complex multidimensional arrays. 
• On the contrary, the attribute .T is an abbreviation of the word transpose and was mainly used for two-dimensional arrays because it is relatively easier for simple operations.

28. What is the difference between np.save() and np.savetxt() ?

Ans:

• The function np.save() dumps a NumPy array to a binary file in .npy format; it is efficient for saving and loading and preserves the array’s data type and, potentially, its shape. 
• As opposed to this, np, save txt () saves an array to a text file; while it is human-readable, it doesn’t preserve data type or shape information nearly as well as the binary format. 
• This difference makes np. Save () is preferable regarding performance and data integrity, while np. Save txt () is useful for exporting data in an accessible textual format.

29. What are the most common performance pitfalls when using NumPy?

Ans:

Common mistakes for performance calls in NumPy are overusing Python loops instead of vectorized operations, which would lead to very slow performances. Another error is the generation of large intermediate arrays during operations, which consumes much more memory. Also, proper broadcasting may lead to efficient computation. Finally, in applying operation, incompatible data types or shapes would stimulate unnecessary type conversion that causes slowing performance.

30. What are vstack() and hstack() in NumPy?

Ans:

‘stack ()’ and ‘stack ()’ are NumPy functions used for stacking arrays vertically or horizontally. 

• ‘vstack()’: This function stacks arrays in sequence along the vertical axis (row-wise). It accepts a tuple or list of arrays and returns a new array with the input arrays placed one on top of the other.
• ‘stack ()’: Conversely, this function stacks arrays along the horizontal axis (column-wise). It combines the input arrays side by side, resulting in a new variety that merges their columns.

31. What is the difference between np.concatenate() and np.stack()?

Ans:

The function np. Concatenate () combines two or more arrays in such a way that depends on an existing axis, thus flexible with the combination of arrays of the same shape. On the other hand, np. Stack () creates a new axis in the resulting array with the constraint that this must be similar to input arrays. This implies that stack() is ideal for data reorganization along a new dimension. And where arrays are to be merged along a defined dimension then concatenate() is applicable.

32. What is the shape of a NumPy array?

Ans:

The shape of a NumPy array is simply the dimensions of an array, written as a tuple that tells the size of each dimension. For example, a 2D array with 3 rows and 4 columns would be (3,4). Knowing the shape helps manipulate the data correctly and make correct computations since many operations require compatible dimensions. To access the shape of an array, you use the attribute .shape on the variety.

33. What are the data types for NumPy?

Ans:

• NumPy supports various data types. The standard types are integers, floats, complex numbers, Boolean types, strings, and more complicated structures like the object type. 
• The structured arrays add to that list, offering support for user-defined data types and, hence, supporting heterogeneous types in data representation. 
• This provides for efficient memory usage and also leads to optimizations in calculations.

34. What does dtype do in a NumPy array?

Ans:

• The type attribute of a NumPy array represents the type of elements, which is an important factor in memory allocation and optimizing performance. 
• So, if the data type is determined when establishing the array, NumPy can guarantee that the array’s contents are stored and computed efficiently. 
• The type can be set when an array is created and can be various, such as integers, floats, or user-defined types. 
• Remembering the type is essential in managing your data’s precision and efficient computation performance.

35. How can a NumPy array’s maximum and minimum values be found?

Ans:

A NumPy array’s maximum and minimum values can be found using np. Max () and np. Min () functions, respectively. These functions run along the array for maximum and minimum values. More than that, we might use np. Amax () and np. Main () functions for the same results. Further, it can also be found along specific axes using the axis parameter of these functions, leading to a more complex analysis of the multidimensional arrays.

36. How does one calculate an array’s mean, median, and standard deviation in NumPy?

Ans:

You use the following methods to obtain a NumPy array’s mean, median, and standard deviation: These return the desired statistic if called on with an array as an argument. Suppose you specify an axis parameter for each of these functions. In that case, you can carry out all calculations along particular axes: this means you can take advantage of their power to analyze statistical structure while still leaving the overall structure of the array.

37. How is the inverse of a matrix computed in NumPy?

Ans:

• NumPy’s function np computes the inverse of a matrix.linalg.inv(). It will accept a square matrix and return the inverse of that if it exists. 
• So, singular matrices raise an error since they have no inverse. 
• Hence, checking for squares and having a nonzero determinant for inversion are important because they decide the existence of an inverse.

38. How is the determinant of a matrix computed in NumPy?

Ans:

• The function that computes the determinant of a matrix is ‘np.linalg.det()’. It takes a square matrix as input and calculates its determinant, returning a scalar value. 
• The determinant is a significant property in linear algebra because it indicates whether a matrix is invertible (a nonzero determinant) and provides insights into its geometric properties. 
• The determinant can also be used to assess the volume scaling factor of transformations represented by the matrix.

39. How does np.memmap() manage large datasets?

Ans:

The function np. Mem map () supports memory-mapped file access, so it handles large datasets that may not completely fit into memory. An array object is created mapping to a file located on the disk, where the data can be manipulated just like in memory, loading chunks of data as needed. This approach reduces memory usage and provides readability and w-writable operations while handling massive data.

40. What is NumPy’s role in scientific computing?

Ans:

NumPy is like a gateway to scientific computing; it has huge power structures and functions for performing numerical analysis with big data sets and complex mathematical operations. The array-oriented model allows fast vectorized computations, while the explicit loops are thus reduced, making this a more performance-oriented model. It can also act as the base for numerous other scientific libraries like SciPy and Pandas and easily lead to a big ecosystem for scientific computing and data analysis.

41. How does NumPy manage multidimensional arrays?

Ans:

• NumPy manages multidimensional arrays very efficiently using a uniform array object called ndarray. This object supports operations across multiple dimensions and allows users to compute things in matrices, tensors, and higher-dimensional data. 
• It has an extensive range of functions available for indexing, slicing, and reshaping, which allows flexible manipulation of multidimensional data structures while maintaining efficiency in terms of memory usage and processing performance.

42. What is the np. where() function?

Ans:

• The np. where() function is useful in NumPy for many purposes, such as condition-based selection and filtering elements in an array. 
• It can return the indices of elements that satisfy a specified condition or produce an array in which values are selected based on conditions from two given arrays. 
• This adds more capability to manipulate data to permit efficient conditional operations and modifications to array elements based on their indices.

43. What is the difference between a structured array and an ordinary NumPy array?

Ans:

The right array is a NumPy array that may store different data types in its elements, effectively representing a composite data structure. In a structured array, all elements could be of various kinds, like database records or table rows. A regular NumPy array can only store data for homogeneous kinds; all elements must belong to the same type. Such a characteristic makes structured arrays particularly useful for complex representations of data.

44. How is an array reshaped in NumPy?

Ans:

A NumPy array can be reshaped using the function np. Reshape () changes an array’s shape without changing its data. The new shape must be compatible with the original array’s size so the total number of elements stays constant. The reshape method can also be called directly on the array object. Reshaping is an important preprocessing step before accessing many operations, such as matrix multiplication and broadcasting.

45. How does it perform memory allocation in NumPy?

Ans:

• NumPy uses contiguous chunks of memory to store its array of objects that accelerate the performance of operations. An array object holds data in one block of memory while creating it so that NumPy can access and manipulate all the data immediately. 
• A contiguous memory layout is useful for vectorized operations and gives access to lower-level optimizations. 
• To facilitate memory management, NumPy provides functions like np. Empty () for arrays that have not been initialized and np. Mem map () for memory-mapped files.

46. What is an order parameter in NumPy functions?

Ans:

• One of the most famous NumPy functions involves its order parameter, used for row-major ordering, also known as C-style or column-major order, often referred to as Fortran-style. 
• This parameter is significant for performance optimization when accessing or changing arrays since it corresponds to the actual data layout in the memory. 
• Through applying an order parameter, people could be sure that compatibility with other libraries would be preserved and thus find optimization of their performance on certain apps, which often operate with multidimensional arrays.

47. How does numpy handle broadcasts for arrays with potentially differing numbers of dimensions?

Ans:

NumPy automatically makes the dimensions of smaller arrays such that they fit into the larger ones at run-time and take care of broadcasting. It is useful for performing element-wise operations on arrays of various shapes without having to make explicit replication of data. Now, broadcasting follows some rules, like alignment of dimensions from the trailing end and expansion of dimensions of size 1. Much more concise codes can be used for efficient operations on arrays of varied sizes.

48. What’s the difference between np. Ix_() and the traditional indexing mechanism?

Ans:

The np. ix_() function generates a mesh grid for advanced indexing in NumPy to assist in selecting the elements from various dimensions of an array at once. It facilitates the easy creation of the Cartesian product of indices, which may simplify the task when searching several dimensions simultaneously. Standard indexing allows direct access to elements with either slice notation or index arrays used directly. It is very good with selecting subarrays in multidimensional data and makes data handling flexible much better.

49. What does the keyword argument axis in NumPy functions mean?

Ans:

• The axis of a NumPy array refers to the dimension along which an operation is performed. It determines the direction for operations like summation or calculating the mean in multidimensional arrays, making it a crucial concept. 
• Specifying ‘axis=0’ means the operation will be executed column-wise, while ‘axis=1’ indicates it will be row-wise. Understanding how axes work allows for more effective data manipulation and analysis. 
• Additionally, this knowledge is vital for ensuring that operations yield the desired results when dealing with complex datasets.

50. What are some common applications of NumPy in data analysis?

Ans:

• NumPy is widely applied in data analysis, mainly for computations on numbers, data manipulation and preprocessing. 
• It also supports operations such as statistical analysis, matrix calculations, and efficient handling of large datasets. 
• Besides, it helps out with issues related to data cleaning and feature transformation and prepares data for machine learning models; therefore, it is a high-utility tool used by data analysts.

51. How does it work with other libraries like Pandas and Matplotlib?

Ans:

NumPy is the foundation upon which many scientific computing libraries stand, including Pandas and Matplotlib. Pandas itself further layers on top of NumPy with data structures such as the DataFrame that utilize NumPy arrays for effective data handling. Matplotlib uses a NumPy array to plot data and allows users to visualize the analysis results based on NumPy seamlessly and at high performance.

52. What are the main functions of the NumPy library?

Ans:

The library’s main functions include array creation and manipulation, mathematical operations, linear algebra, and statistical operations. In other words, it provides reshaping functions for arrays, element-wise operations, data aggregation along dimensions, and support for random number generation. These features make it a versatile library for numerical computations. Additionally, its efficiency and ease of use have made it a popular choice for both beginners and experienced users in scientific computing and data analysis.

53. How does NumPy help in big array calculations?

Ans:

• For big matrices, NumPy further accelerates computations using vectorization, which is the ability to perform batch operations along an entire array rather than at the element level. 
• This introduces relatively lesser overhead regarding Python loops and, therefore, improves performance by taking advantage of the low-level implementations. 
• Additionally, NumPy optimizes memory use and relies on contiguous memory layouts, which minimize data access time and accelerate computations involving large-scale datasets.

54. What does the ndarray object represent in NumPy?

Ans:

• The array object is NumPy’s central data structure. It is an abbreviation for a multidimensional array with fixed-size items. 
• It offers an extremely powerful and flexible way of storing and manipulating numerical data and allows for a wide range of operations, such as indexing, slicing, and broadcasting. 
• The array object is built for efficient performance, making it crucial for numerical computing and data analysis tasks.

55. How do users can sort a numpy array?

Ans:

The function ‘np. Sort ()’ sorts a NumPy array and returns a new sorted array. Alternatively, the ‘sort()’ method is available for the array object, allowing it to have some kind in place. Sorting can also be performed along a specified axis, with additional parameters for customizing the sorting algorithm and order, whether ascending or descending. This flexibility makes sorting efficient and adaptable to various data analysis needs. Furthermore, NumPy’s sorting functions are optimized for performance, enabling quick operations even on large datasets.

56. How can one access the elements of a NumPy array?

Ans:

All elements of a NumPy array can be accessed using indexing and slicing methods. Single elements can be retrieved by specifying their index, while colon notation allows for the extraction of slices of elements. Additionally, multidimensional arrays support advanced indexing by specifying a tuple or a variety of indices to retrieve particular rows, columns, or sub-arrays. This capability enhances the flexibility of data manipulation and analysis. Moreover, combining these indexing techniques enables efficient data retrieval tailored to specific analytical needs.

57. What does np. unique() do?

Ans:

• The call to the ‘np. Unique ()’ function finds the unique elements from a given NumPy array, effectively removing duplicates. It can also provide additional information, such as the indices of distinctive elements and their counts. 
• This function is particularly useful in data analysis, especially for summarizing categorical data or identifying distinct values within datasets. 
• Furthermore, its ability to handle multidimensional arrays makes it a valuable tool for ensuring data integrity and exploring unique data characteristics across various dimensions.

58. What are the characteristics of a structured NumPy array?

Ans:

• A NumPy structured array is structured to hold heterogeneous data types within its elements. It’s almost like a table or a database record where elements can be composed of multiple fields with different data types. 
• It lets data representations become sophisticated through complex multidimensional data structures. 
• Structured arrays support operations such as indexing and slicing and maintain the integrity of individual fields with named fields for easier access to the data.

59. How is np.hstack() different from np.vstack()?

Ans:

The function np. Stack () stacks arrays vertically, adding rows from the input arrays to create a new variety with an increased number of rows. On the other hand, np. Stack () stacks arrays horizontally by joining the columns of the input arrays to produce a new variety with an increased number of columns. Therefore, the choice between these functions depends on whether the data arrangement in view is vertical or horizontal.

60. How can rolling averages be computed with NumPy?

Ans:

Rolling averages in NumPy can be calculated using the ‘np. Convolve ()’ function with the appropriate window size or manually through a for loop that computes averages over a specified interval. This approach effectively smooths time series data and highlights trends by averaging values over defined windows. Additionally, rolling averages help mitigate the effects of short-term fluctuations, providing a clearer view of long-term trends.

61. What does np.flatnonzero() do?

Ans:

• The function ‘np. Flat nonzero ()’ returns the indices of nonzero elements in a flattened version of a NumPy array, making it useful for quickly locating nonzero entries. 
• This capability allows for efficient data manipulation and analysis, especially in sparse data situations. 
• Additionally, it can enhance performance by minimizing the need for looping through elements, thereby streamlining operations on large datasets with prevalent zero values. 
• This functionality is particularly valuable in fields like machine learning and data science, where sparse matrices are common.

62. What does the value np. Nan mean in NumPy?

Ans:

• The term np. Nan stands for “Not a Number” and represents missing or undefined values in a NumPy array. 
• This is important when dealing with incomplete datasets and calculating them without considering missing values. 
• NumPy provides various functions to detect, manipulate, and ignore np. Nan values in the calculations so that no data analysis goes wrong.

63. How does NumPy handle missing data?

Ans:

Missing data might then be denoted using np. Nan, or through masked arrays in NumPy arrays. Functions are available in NumPy, which can be used without regard for the existence of np. Nan values, such that there is a choice of computing the whole data. Masked arrays explicitly flag certain values as invalid, with which one would want to execute more advanced methods of handling missing data when computing.

64. What does the np. Clip () function do?

Ans:

The function np. Clip () limits the values in a NumPy array to fall within a given range. If there are values that are less than a specified minimum, then that minimum is assigned to them. If there are values that are more than a specified maximum, then that maximum is assigned to them. This is very important in data normalization and the fact that values need to lie within acceptable limits for analysis or visualization.

65. How is the generation of random numbers in NumPy performed?

Ans:

• To generate random numbers in NumPy, the ‘np.random’ module is utilized. This module contains various functions for producing random values from different distributions, such as uniform, normal, binomial, and others. 
• These functions are particularly useful for creating random arrays and samples for simulations and other statistical modelling purposes. 
• Additionally, the ‘np. Random’ module’s flexibility allows users to customize the size and shape of the output, making it an essential tool for testing algorithms and conducting experiments in data analysis.

66. What is the role of np.random.seed()?

Ans:

The function np. Random. Seed () seeds the random number generator in NumPy to get a reproducible sequence of random numbers. For example, it can be used to set the seed value to guarantee that every time the code is executed, the same sequence of random numbers is obtained; this can be useful in debugging and repeated experiments for the same results.

67. How are the elements of an array shuffled in NumPy?

Ans:

The function ‘np.random.shuffle()’ applied to a NumPy array will rearrange its elements randomly in place. This ensures that the overall structure of the dataset remains preserved while the order of elements is randomized, as this function directly modifies the original array. Additionally, this feature is particularly useful in data preparation for machine learning tasks, where shuffling can help eliminate biases and improve the robustness of models by ensuring diverse training samples.

68. What is the keepdims parameter used in NumPy functions for?

Ans:

• The keep-dims parameter in most NumPy functions prevents the dimensions of the array from being disturbed after summation or similar operations. 
• If this parameter is set to True, it ensures that the number of dimensions within the result remains the same as in the input array, making broadcasting and maintaining data shape through future calculations feasible.

69. How can elements of an array be filtered based on a condition?

Ans:

• Elements of a NumPy array can be filtered using a boolean condition to create a mask. This process returns a boolean array of the same shape, where ‘True’ indicates the elements that meet the specified condition. 
• Elements that satisfy the filtering can then be extracted from the original array using this boolean array as indices. 
• This method is highly efficient for selective data retrieval, allowing for easy manipulation and analysis of specific subsets of data without needing explicit loops. 
• Additionally, it enhances code readability and conciseness, making data operations more intuitive.

70. What does the np. Concatenate () function do?

Ans:

The ‘np. The concatenate ()’ function combines two or more arrays along a specified axis to create a new variety. This function is highly flexible, allowing concatenation across any dimension, provided that the other dimensions share compatible shapes among the input arrays. It is particularly useful for managing datasets or adding elements efficiently. Additionally, this functionality simplifies data manipulation tasks, making assembling or extending arrays for analysis in various scientific and engineering applications easier.

71. How does NumPy support mathematical operations on arrays?

Ans:

NumPy supports many mathematical operations on arrays, ranging from element-wise calculations to matrix multiplication and analysis or statistical operations. For such operations, you can use some built-in functions or operators, allowing pretty efficient computations with large datasets while taking advantage of optimized performance under the hood.

72. What is the np. Tile () function used for?

Ans:

• The function ‘np. Tile ()’ repeats an array a specified number of times along each axis. In other words, it returns a new array by replicating the input array. 
• This function is often useful for generating patterns or extending data dimensions to facilitate broadcasting calculations. 
• Additionally, it can help create large datasets from smaller ones, making it easier to perform experiments and simulations in data analysis and scientific computing.

73. How does np.meshgrid() differ from np.ogrid()?

Ans:

• Np. mesh grid () is a function that generates coordinate matrices from coordinate vectors, where it returns arrays ready to be called in a grid to evaluate functions. 
• It produces two-dimensional grids for each of the input vectors. On the other hand, np. Grid () produces open grids, returning arrays that consume less memory because they return one-dimensional arrays. This makes broadcasting favourable without needing full grids.

74. What are some other advantages of using NumPy for numerical computations?

Ans:

Using NumPy for numerical computations offers significant benefits regarding memory management, optimized performance through vectorized operations, and support for various mathematical functions. It allows for manipulating multidimensional arrays, and its compatibility with other libraries makes it an invaluable asset for scientific computing and data analysis. Furthermore, its extensive community support and documentation provide users with resources and tools that enhance productivity and facilitate learning, making it a popular choice among researchers and developers.

75. How can unique elements within a NumPy array be identified?

Ans:

The cumulative sum of the elements in a NumPy array can be computed using the function ‘np. cumsum()’. This function returns an array in which each element represents the total of all preceding elements, making it useful for accumulating values and applicable in trend analysis of time series data. Additionally, it helps identify patterns and shifts over time, providing insights into data behaviour that can be critical for forecasting and decision-making.

76. What is the transpose of a NumPy array?

Ans:

• A NumPy array can be transposition using either the ‘np. Transpose ()’ function or the ‘.T’ attribute. This allows the axes of an array to be exchanged, turning rows into columns and vice versa. 
• This capability is particularly useful for matrix operations and reshaping data for analysis purposes. 
• Additionally, transposing arrays can enhance computational efficiency in various algorithms, facilitating smoother execution of linear algebra operations and improving data handling in multidimensional datasets.

77. What does np. isfinite() do?

Ans:

• The ‘np.isfinite()’ function checks for finite values in an array, returning a boolean array of the same shape where ‘True’ indicates finite numbers, excluding NaN or infinity. 
• This functionality is especially useful during validation and cleaning steps, as it ensures that operations are performed only on valid numerical entries. 
• Furthermore, it helps maintain data integrity by easily identifying and filtering out problematic values, thereby enhancing the reliability of subsequent analyses and computations.

78. What are the main features of NumPy that facilitate scientific computing?

Ans:

The dot product of two arrays can be computed using the ‘np. dot()’ function or the ‘@’ operator in NumPy. This operation multiplies the corresponding elements of two arrays and sums the results, making it crucial in linear algebra and various applications, including machine learning. Additionally, it is a fundamental building block for many mathematical operations, such as calculating projections and determining the similarity between vectors, which are essential in optimizing algorithms and data analysis.

79. What does the np. Median () function do?

Ans:

The ‘np. The median ()’ function calculates the median of a NumPy array, representing its central tendency. The median is particularly useful in situations with skewed distributions or outliers, as it may serve as a more robust indicator than the mean in statistical analyses. Moreover, using the median can provide a clearer picture of data distribution, helping to identify trends and patterns that extreme values might obscure. This makes it an essential tool for data scientists and analysts working with diverse datasets.

80. How can the QR decomposition of a matrix be calculated in NumPy?

Ans:

• A NumPy array contains unique elements that can be found using the np. unique() function. It returns all unique values of the elements in the array. 
• The function can also return other outputs, such as the indices of the unique elements and their counts, which are very helpful when performing data analysis and summarization.

81. What does the function do in np.array_equal()?

Ans:

• The function ‘np.array_equal()’ checks whether two arrays are identical in both their shape and their elements, returning a boolean value that indicates equality. 
• This function is particularly useful for verifying the correctness of results from numerical computations or comparing datasets. 
• Additionally, it can aid in debugging by ensuring that operations on arrays yield the expected outcomes, thereby enhancing confidence in the integrity of the data analysis process. 
• This feature makes it an essential tool for developers and researchers with complex array manipulations.

82. What does NumPy contribute to machine learning?

Ans:

NumPy is crucial to machine learning as it offers efficient data structures and the mathematical functions needed for numerical computation. It supports operations on huge data sets, assists in preprocessing the data and serves as the basis for other machine learning libraries like TensorFlow and sci-kit-learn. Furthermore, its ability to handle multidimensional arrays allows for easy data manipulation in various formats, enhancing model development and experimentation flexibility.

83. What are the main features of NumPy that facilitate scientific computing?

Ans:

State the key capabilities of NumPy that allow scientific computing the Python library NumPy offers multidimensional array support, an extensive library of mathematical functions, optimized performance through vectorization, support for broadcasting, and tools for linear algebra and statistical analysis. Researchers and data scientists must consider the necessity of using NumPy.

84. What is the difference between np.arange() and np.linspace()?

Ans:

• The np. arrange () function returns a range of evenly spaced values over a specified interval with a given step size. 
• In contrast, the np. linspace() function returns a specified number of evenly spaced values between two endpoints. It is, therefore, suited to situations requiring specific control over the number of elements in the output array. 
• Additionally, while ‘np.arange()’ is more flexible with its step size, ‘np.linspace()’ is particularly useful for generating points in scenarios like plotting, where precise control over the number of points is crucial.

85. How can the QR decomposition of a matrix be calculated in NumPy?

Ans:

• Use the function np.linalg.qr() that performs QR decomposition it factors a matrix into an orthogonal matrix Q and an upper triangular matrix R. 
• Such decompositions are useful for solving systems of linear equations and least squares problems in numerical linear algebra. 
• Moreover, QR decomposition is also commonly used in algorithms for eigenvalue computation and methods like the Gram-Schmidt process for orthogonalization.

86. What is the difference between a view and a copy in NumPy?

Ans:

A view in NumPy is an array that points to the same data buffer as the original array. Changes to the view alter the original data. A copy creates an all-new array with a separate data buffer. This implies that the modifications made to the copy will not affect the original array, so it is critical to know this when managing memory wisely. Understanding the difference between views and copies is essential for optimizing performance, as views can save memory and computational resources when working with large datasets.

87. What does the function np. Nonzero () do?

Ans:

The function np. Nonzero () finds out indices of the nonzero elements in the given array, thus efficiently allowing it to hunt down elements satisfying a given condition. It’s particularly useful when doing data analysis and manipulation tasks that often have sparse data representations. Additionally, the output of ‘np. Nonzero ()’ can be used to create masks for filtering or selecting elements from the original array based on specific criteria.

88. How can a random integer within a specified range be generated in NumPy?

Ans:

• A function, np. Random. randint() returns one or more random integers within a specified range. This function takes in three parameters: the range’s low and high bounds and the output’s size. It’s useful for generating random samples in simulations or random selections in algorithms.
• NumPy is an instrument for efficiently implementing data visualization to create rapid numerical tools, which are the basics of graphical representation. 
• These mighty array structures help facilitate smooth data handling and reduce the complexity of working with large amounts of data. 

89. What are some common NumPy functions to take advantage of statistical analysis?

Ans:

• NumPy has various critical functions accessible to perform statistical analysis, including np. Mean (), np. Median (), and np. Std (), which computes average, median, and standard deviation values. Np. Var () provides a variance calculation to estimate data variability. 
• Functions like np. Percentile () helps identify specific cutoffs in the data, and np. Histogram () is useful for understanding the distribution of data. 
• Together, these functions form an overall toolbox for analyzing and interpreting numerical data. These toolkits help researchers and analysts extract meaningful knowledge from datasets.

90. How can data be imported from a CSV file into a NumPy array?

Ans:

The function np. loadtxt() or np. genfromtxt() will import data from a CSV file directly into a numpy array, but they are built for reading the structured text files. They convert text data into NumPy objects, making it easier to manipulate and analyze. In the case of np. loadtxt(), the user primarily sets delimiters and data type. Np. genfromtxt() offers more flexibility in effectively handling missing values. This makes it particularly well-suited for heterogeneous datasets, where different columns may contain various data types. 

91. What is the difference between np.loadtxt() and np.genfromtxt()? 

Ans:

Np. load txt () is optimized for well-structured numeric data and faster for simple cases. It’s great when the dataset has consistent formatting. It does not handle missing values; if the dataset is imperfect, it may become problematic. On the contrary, functions in np. genfromtxt() has variations where datasets with missing values can be interpreted by providing options for fill values and data types. It’s thus more preferred for working with complex or irregular data structures. 

92. How can multiple arrays be saved into a single file using NumPy?

Ans:

• Multiple arrays can be saved several arrays in one file using the np. savez() or np.savez_compressed() functions that allow effective storage and retrieval. 
• These functions create an archive file that contains several arrays, helping users store related datasets. When saving, every array can be assigned a unique name, which makes access much easier afterwards. 
• Upon loading the data, users can refer to individual arrays by name and easily extract specific datasets. 
• This approach is useful, especially in managing complex projects with varied datasets where access needs to be stored together. In general, this improves data management in NumPy.

93. How does NumPy handle very large datasets that are too large to be loaded into available memory?

Ans:

• NumPy can handle a vast amount of datasets by allowing access to array segments stored on disk through memory-mapped files using the np. Mem map () function. 
• This technique allows operations on large arrays without incurring the expense of loading the entire data set into memory, thus saving many a byte. 
• It uses memory mapping, so any data set too big to fit into RAM can be operated upon while maintaining NumPy performance. 
• One can read and write data on demand, thus allowing efficient data processing in constrained environments. 

94. What is the function np. from function ()?

Ans:

• The function creates an array by executing a given function over an index grid, thus allowing flexible, complicated array generation. 
• This feature is particularly useful when creating structure arrays that depend on mathematical expressions or certain conditions. 
• For example, it helps define a function that fills an array according to its coordinates and thereby permits the creation of such patterns or geometries. 
• It reduces the effort required to produce arrays, depending on their position values, hence raising productivity in numerical calculations. 

95. What are the best practices in making efficient use of NumPy?

Ans:

To fully utilize efficiency, one should use efficiencies in NumPy. Instead of using tradition-based loops, vectorized operations should be used because they significantly improve performance. The types chosen for an array’s data play a significant role in optimizing both memory usage and computation speed. In addition, data copying redundancy can be eliminated by making reference calls to arrays instead of copying them. Built-in NumPy mathematical function operations also reduce the complexity and number of processes since they work as single-line codes. 

96. How can the gradient of a function be computed using NumPy?

Ans:

It is possible to compute the gradient of a function with the help of the np. The gradient () function estimates each NumPy array’s derivative at each point. This is a versatile function since it can handle various spacings between points to provide an approximate derivative. By applying this function, one will be able to know how functions are varied and thus find easy ways to use them in numerical analysis and optimization contexts. The gradient is an essential concept in areas like physics and engineering, as it gives an idea about rates of change. 

97. What is the significance of the np. Save () function when saving multiple arrays?

Ans:

This means saving multiple NumPy arrays in a compressed file with an np function. Save (), allowing a clean archive of related datasets. Thus, this method can be applied to manipulate arrays more effectively and may prohibit much clutter and confusion during retrieval. While saving the variety, each can be assigned an especially given name. During the loading operation, it will be accessible through the same name. The archive is so arranged that it allows easy retrieval of individual arrays by their assigned names at access time.