Types of Trees in Data Structure Guide with Examples

Binary Search Trees (BST)

• A Binary Search Tree (BST) is a binary tree with the additional property that the left subtree of a node contains only nodes with values less than the node, and the right subtree contains only nodes with values greater than the node.
• This property enables efficient search, insertion, and deletion operations in O(log n) time for balanced BSTs. However, if the BST becomes skewed (like a linked list), the time complexity can degrade to O(n). BSTs are widely used in search-intensive applications and are the basis for many other trees.



Would You Like to Know More About Cloud Computing Course? Sign Up For Our Cloud Computing Course Now!




AVL Trees

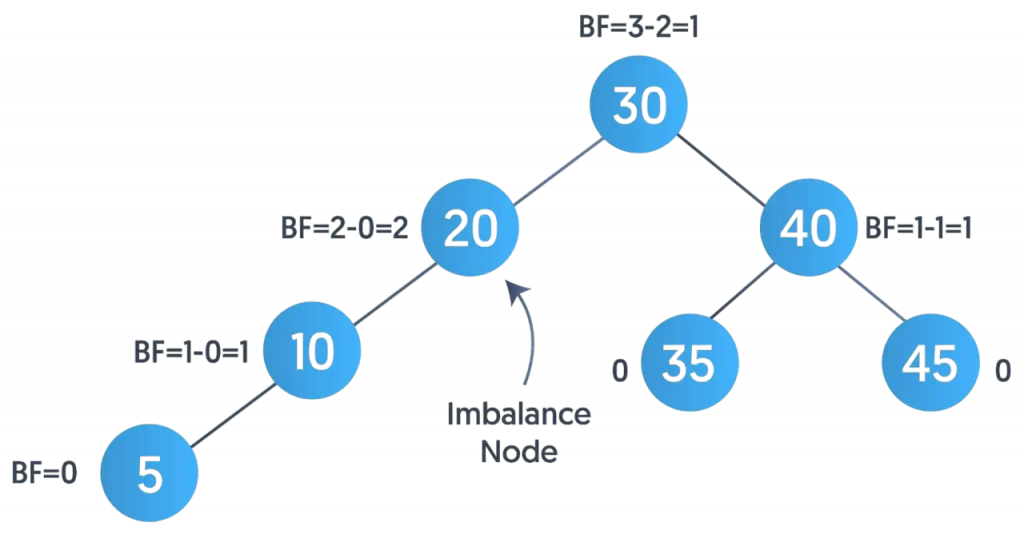
• An AVL Tree is a self-balancing binary search tree, named after its inventors Adelson-Velsky and Landis. In an AVL tree, the difference in height between the left and right subtree (called the balance factor) of any node is strictly maintained as -1, 0, or 1. If an insertion or deletion operation violates this balance, rotations (left, right, or double) are performed to restore it.
• This ensures that the tree remains balanced, with O(log n) time complexity for all basic operations, making AVL trees suitable for real-time systems and applications requiring frequent updates.



Develop Your Skills with Cloud Computing Course Certification Course

Weekday / Weekend BatchesSee Batch Details

Red-Black Trees

A Red-Black Tree is another type of self-balancing BST, which enforces a different set of rules to maintain balance using node colors (red or black). These rules include:

• The root is always black.
• Red nodes cannot have red children (no two reds in a row).
• Every path from a node to its descendant null nodes must have the same number of black nodes.

Red-Black Trees may not be as strictly balanced as AVL trees, but they offer faster insertions and deletions in practice due to fewer rotations, making them the preferred structure in many libraries like the C++ STL map and Java TreeMap.

B-Trees and B+ Trees

B-Trees are generalizations of binary search trees that can have more than two children per node. They are designed to minimize disk reads and are commonly used in databases and file systems. Each node contains multiple keys and can have several children, allowing for higher branching and reduced tree height. B+ Trees extend B-Trees by storing all values at the leaf level and maintaining a linked list of leaf nodes. This makes range queries and sequential access much more efficient. B+ Trees are the default indexing structure in most relational databases due to their performance on disk-based storage.

Trie (Prefix Trees)

A Trie, or prefix tree, is a multi-way tree structure used to store strings or sequences, with each node representing a character. Tries are highly efficient for prefix-based searches, autocomplete features, and dictionary implementations. Each path from the root to a leaf node corresponds to a string in the dataset. They offer O(L) search time for strings of length L, regardless of the number of stored words. Tries consume more memory than hash tables but support ordered traversal and prefix operations more effectively.




Are You Interested in Learning More About Cloud Computing Course? Sign Up For Our Cloud Computing Course Today!




Splay Trees

A Splay Tree is a self-adjusting BST where recently accessed elements are moved to the root via splaying (a series of tree rotations). The idea is to improve the access time for frequently used elements, making future accesses faster. Though worst-case operations can still take O(n) time, the amortized time is O(log n). Splay trees are useful in caching scenarios and where temporal locality is expected.




Preparing for Cloud Computing Job Interviews? Have a Look at Our Blog on Cloud Computing Interview Questions and Answers To Ace Your Interview!




Tree Traversal Techniques

Tree traversal refers to visiting all the nodes in a tree in a specific order. The main types include:

• Inorder Traversal (Left → Root → Right): Commonly used in binary search trees (BSTs) to retrieve sorted data.
• Preorder Traversal (Root → Left → Right): Useful for copying trees or generating prefix expressions.
• Postorder Traversal (Left → Right → Root): Ideal for deleting trees or evaluating postfix expressions.
• Level Order Traversal (Breadth-First): Traverses nodes level by level using a queue.

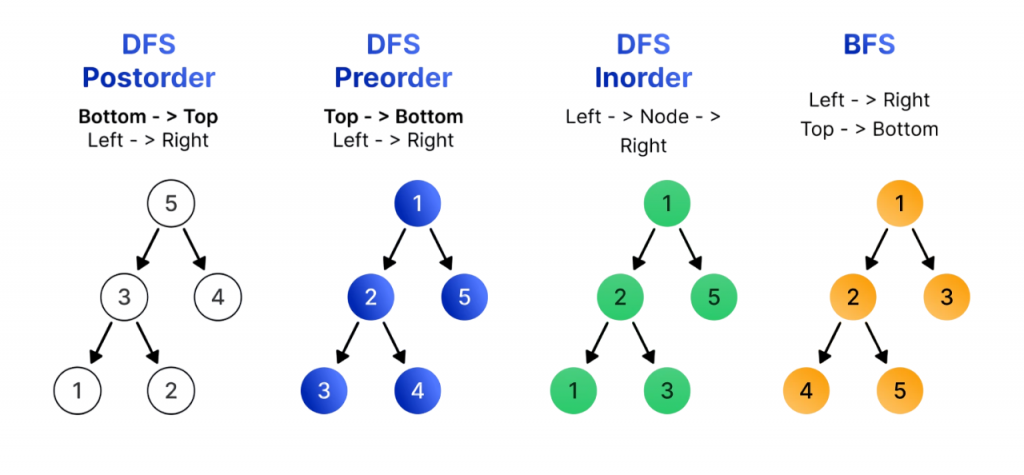
Traversal techniques are essential for implementing search algorithms, evaluating expressions, and generating tree-based representations.






Applications in Computing

Trees are foundational data structures used across a wide range of domains:

• Binary Search Trees: Enable efficient searching and sorting operations.
• Tries: Power auto-complete, spell checking, and IP routing systems.
• Segment Trees: Support efficient range queries in arrays.
• B-Trees: Used for indexing in databases and file systems.
• AVL/Red-Black Trees: Implement ordered maps and sets in standard libraries.
• Expression Trees: Facilitate evaluation and representation of arithmetic expressions.
• Decision Trees: Applied in machine learning for classification and regression tasks.
• XML/HTML Parsing: Represent hierarchical structure of documents.

Understanding tree types enables optimized solutions in data storage, searching, compression, artificial intelligence, and more.






Summary

hierarchical ways to store and manipulate data. From simple binary trees to advanced structures like AVL trees, B+ trees, Tries, and Splay trees, each type addresses a specific computational requirement. A strong grasp of the different Types of Trees in Data Structures is essential for algorithm design, database indexing, system development, and competitive programming. Choosing the right structure depends on the application’s needs whether it’s balance, search speed, update frequency, or disk access optimization. By mastering the various Types of Trees in Data Structures, developers can design scalable, optimized, and reliable solutions across diverse domains.