
- Introduction to Types of Trees in Data Structures
- Binary Trees
- Binary Search Trees (BST)
- AVL Trees
- Red-Black Trees
- B-Trees and B+ Trees
- Segment Trees
- Trie (Prefix Trees)
- Splay Trees
- Tree Traversal Techniques
- Applications in Computing
- Summary
Introduction to Types of Trees in Data Structures
In computer science, understanding the different Types of Trees in Data Structures is crucial for solving hierarchical data problems efficiently. A tree is a non-linear, hierarchical structure consisting of nodes connected by edges, starting from a root node that branches into child nodes, forming parent-child relationships. To see how such structures are applied in scalable software systems, exploring FullStack With Java Training reveals how tree-based models support efficient data organization, UI rendering, and backend logic across full-stack Java applications. Unlike linear structures such as arrays or linked lists, trees excel at representing hierarchy and allow efficient operations like insertion, deletion, searching, and traversal. Learning the various Types of Trees in Data Structures such as binary trees, AVL trees, B-trees, and red-black trees helps developers choose the right structure for algorithms, databases, and real-world applications where speed and organization are critical.
To Earn Your FullStack With Java Training Certification, Gain Insights From Leading Web Developer Experts And Advance Your Career With ACTE’s FullStack With Java Training Today!
Binary Trees
A Binary Tree is a tree data structure where each node can have at most two children, referred to as the left and right child. It is the foundation of more specialized trees such as binary search trees and AVL trees. Binary trees are commonly used to implement expressions, hierarchies, and parsing structures. To understand how such data structures integrate with modern programming languages, exploring Kotlin vs Java reveals how Java offers mature libraries for tree manipulation, while Kotlin enhances readability and conciseness making both suitable for implementing structured logic in scalable applications. While binary trees can be unbalanced and inefficient in the worst-case scenarios, their structure allows for recursive traversal methods and efficient management of hierarchical data.
Binary Search Trees (BST)
- A Binary Search Tree (BST) is a binary tree with the additional property that the left subtree of a node contains only nodes with values less than the node, and the right subtree contains only nodes with values greater than the node.
- This property enables efficient search, insertion, and deletion operations in O(log n) time for balanced BSTs. However, if the BST becomes skewed (like a linked list), the time complexity can degrade to O(n). BSTs are widely used in search-intensive applications and are the basis for many other trees.
- An AVL Tree is a self-balancing binary search tree, named after its inventors Adelson-Velsky and Landis. In an AVL tree, the difference in height between the left and right subtree (called the balance factor) of any node is strictly maintained as -1, 0, or 1.
- If an insertion or deletion operation violates this balance, rotations (left, right, or double) are performed to restore it. This ensures that the tree remains balanced, with O(log n) time complexity for all basic operations, making AVL trees suitable for real-time systems and applications requiring frequent updates.
- The root is always black.
- Red nodes cannot have red children (no two reds in a row).
- Every path from a node to its descendant null nodes must have the same number of black nodes.
- Inorder Traversal (Left → Root → Right): Commonly used in binary search trees (BSTs) to retrieve sorted data.
- Preorder Traversal (Root → Left → Right): Useful for copying trees or generating prefix expressions.
- Postorder Traversal (Left → Right → Root): Ideal for deleting trees or evaluating postfix expressions.
- Level Order Traversal (Breadth-First): Traverses nodes level by level using a queue.
- Binary Search Trees: Enable efficient searching and sorting operations.
- Tries: Power auto-complete, spell checking, and IP routing systems.
- Segment Trees: Support efficient range queries in arrays.
- B-Trees: Used for indexing in databases and file systems.
- AVL/Red-Black Trees: Implement ordered maps and sets in standard libraries.
- Expression Trees: Facilitate evaluation and representation of arithmetic expressions.
- Decision Trees: Applied in machine learning for classification and regression tasks.
- XML/HTML Parsing: Represent hierarchical structure of documents.
Would You Like to Know More About FullStack With Java Training? Sign Up For Our FullStack With Java Training Now!
AVL Trees
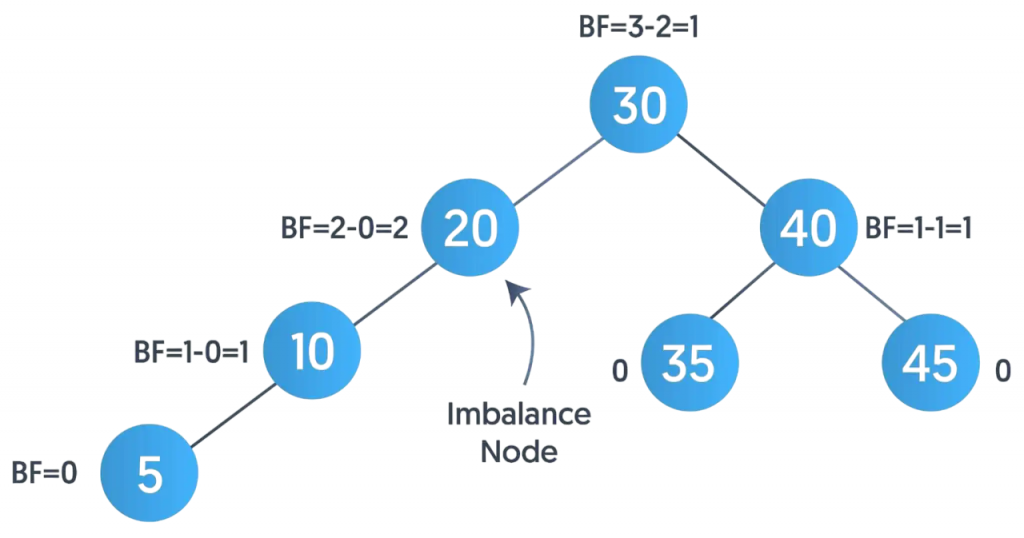
Red-Black Trees
A Red-Black Tree is another type of self-balancing BST, which enforces a different set of rules to maintain balance using node colors (red or black). These rules include: maintaining root blackness, ensuring no two consecutive red nodes, and balancing paths from root to leaves. To understand how such structural enforcement aligns with object-oriented principles, exploring What is Abstraction in Java reveals how abstraction hides internal balancing logic while exposing consistent tree operations promoting modularity and predictable behavior in complex systems.
Red-Black Trees may not be as strictly balanced as AVL trees, but they offer faster insertions and deletions in practice due to fewer rotations, making them the preferred structure in many libraries like the C++ STL map and Java TreeMap.
B-Trees and B+ Trees
B-Trees are generalizations of binary search trees that can have more than two children per node. They are designed to minimize disk reads and are commonly used in databases and file systems. Each node contains multiple keys and can have several children, allowing for higher branching and reduced tree height. To understand how such structures enhance performance in enterprise applications, exploring FullStack With Java Training reveals how multi-way trees like B-trees are used in databases, file systems, and indexing supporting scalable data access across full-stack Java environments. B+ Trees extend B-Trees by storing all values at the leaf level and maintaining a linked list of leaf nodes. This makes range queries and sequential access much more efficient. B+ Trees are the default indexing structure in most relational databases due to their performance on disk-based storage.
Trie (Prefix Trees)
A Trie, or prefix tree, is a multi-way tree structure used to store strings or sequences, with each node representing a character. Tries are highly efficient for prefix-based searches, autocomplete features, and dictionary implementations. Each path from the root to a leaf node corresponds to a string in the dataset. They offer O(L) search time for strings of length L, regardless of the number of stored words. To understand how such efficiency is achieved through structural design, exploring Important Data Structures and Algorithms reveals how tries, trees, and hash-based structures optimize search operations balancing speed, memory usage, and scalability in real-world applications. Tries consume more memory than hash tables but support ordered traversal and prefix operations more effectively.
Are You Interested in Learning More About FullStack With Java Training? Sign Up For Our FullStack With Java Training Today!
Segment Trees
A Segment Tree is a binary tree used for answering range queries and performing range updates in logarithmic time. It’s commonly used in competitive programming and data-intensive applications like gaming, analytics, and time series processing. Segment trees allow querying for sums, minimums, maximums, GCDs, etc., over ranges in an array while supporting updates efficiently. To contrast this with simpler decision-making strategies, exploring How Greedy Algorithms Work reveals how greedy methods make locally optimal choices at each step offering fast, intuitive solutions for problems like interval scheduling, coin change, and activity selection. Though they require more memory (about 4 * n for an array of size n), their power lies in balancing query speed with update speed.
Splay Trees
A Splay Tree is a self-adjusting BST where recently accessed elements are moved to the root via splaying (a series of tree rotations). The idea is to improve the access time for frequently used elements, making future accesses faster. To understand how memory access and variable visibility contribute to performance, exploring Python Scopes and Their Built-in Functions reveals how Python manages local, global, and nonlocal scopes optimizing lookup speed and ensuring predictable behavior in complex codebases. Though worst-case operations can still take O(n) time, the amortized time is O(log n). Splay trees are useful in caching scenarios and where temporal locality is expected.
Preparing for Full Stack With Java Job Interviews? Have a Look at Our Blog on FullStack With Java Training Interview Questions and Answers To Ace Your Interview!
Tree Traversal Techniques
Tree traversal refers to visiting all the nodes in a tree in a specific order. The main types include: inorder, preorder, and postorder traversal each serving different use cases in data processing. To understand how structured access patterns apply beyond trees, exploring Soap vs Rest reveals how SOAP enforces strict message formats and ordered operations, while REST allows flexible, stateless interactions mirroring traversal strategies in API design.
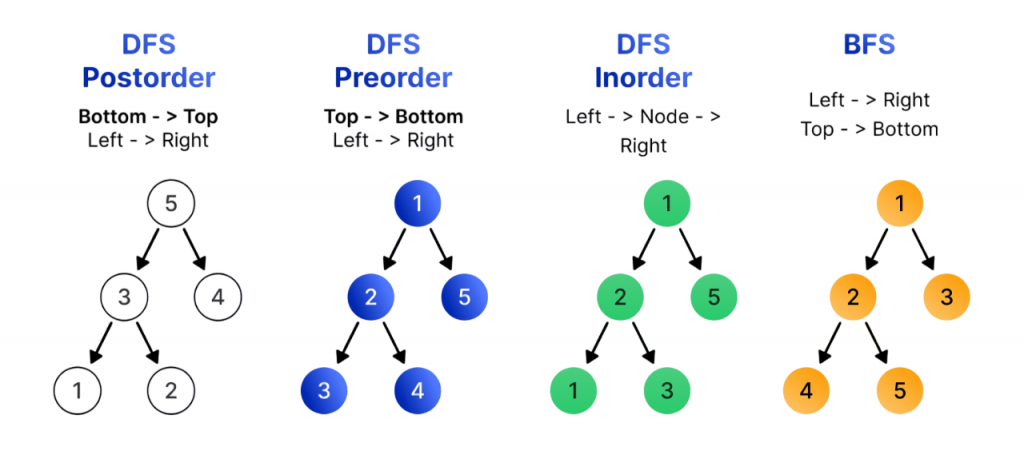
Traversal techniques are essential for implementing search algorithms, evaluating expressions, and generating tree-based representations.
Applications in Computing
Trees are foundational data structures used across a wide range of domains: from compiler design and database indexing to hierarchical modeling and decision-making systems. To efficiently build and debug such structures, exploring Python IDEs and Code Editors reveals how modern tools support tree visualization, syntax-aware navigation, and intelligent code suggestions making complex data structure development more intuitive and error-free.
Understanding tree types enables optimized solutions in data storage, searching, compression, artificial intelligence, and more.
Summary
hierarchical ways to store and manipulate data. From simple binary trees to advanced structures like AVL trees, B+ trees, Tries, and Splay trees, each type addresses a specific computational requirement. A strong grasp of the different Types of Trees in Data Structures is essential for algorithm design, database indexing, system development, and competitive programming. To see how these concepts are applied in real-world projects, exploring FullStack With Java Training reveals how tree structures support efficient data handling, scalable architecture, and optimized search operations across full-stack Java applications. Choosing the right structure depends on the application’s needs whether it’s balance, search speed, update frequency, or disk access optimization. By mastering the various Types of Trees in Data Structures, developers can design scalable, optimized, and reliable solutions across diverse domains.





