
- Introduction to Hamming Distance
- Mathematical Definition
- Binary String Comparison
- Applications in Error Detection
- Hamming Code Basics
- Implementing Hamming Distance in Python/C++
- Differences from Levenshtein Distance
- Bit Manipulation for Hamming Calculation
- Conclusion
Introduction to Hamming Distance
Hamming Distance is a metric for comparing two strings of equal length. It measures the number of positions at which the corresponding symbols differ. Originally introduced by Richard Hamming, this concept plays a fundamental role in information theory, computer science, and telecommunications. It is especially useful for identifying differences between binary strings and ensuring data integrity during transmission. In various domains ranging from bioinformatics to machine learning Hamming Distance provides a simple yet powerful way to quantify dissimilarity.Hamming Distance is a fundamental concept in computer science and information theory, Full Stack Training used to measure the difference between two strings of equal length. Specifically, it counts the number of positions at which the corresponding characters in the two strings are different. Originally introduced by Richard Hamming, this concept is widely used in fields such as error detection and correction, data transmission, cryptography, and bioinformatics. For example, in binary strings, the Hamming Distance between “10101” and “10011” is 2, because they differ in two bit positions. The smaller the Hamming Distance, the more similar the two strings are. In communication systems, this property is crucial for detecting and correcting transmission errors. By calculating the Hamming Distance between received and expected data, systems can identify and even fix certain types of errors without retransmission. Hamming distance is also used in genetics (e.g., comparing DNA sequences), machine learning (e.g., measuring feature vector similarity), and other areas where similarity measurement is important. It’s efficient to compute and easy to implement in any programming language Hamming Distance , making it a popular tool for comparing strings, binary data, or sequences in a wide variety of applications.
Interested in Obtaining Your Full stack Certificate? View The Full Stack Developer Course Offered By ACTE Right Now!
Mathematical Definition
Formally, the Hamming Distance between two strings of equal length is the number of positions where the characters differ. For example, given two binary strings s1 = “1011101” and s2 = “1001001”, the Hamming Distance is 2, since they differ at the second and fourth bits. Mathematically, it can be defined as:
H(s1, s2) = ∑ (s1ᵢ ≠ s2ᵢ) for all i in length of s1,
This summation counts the number of mismatches. It’s important that both strings are of equal length; otherwise, Reverse a String the Hamming Distance is undefined.
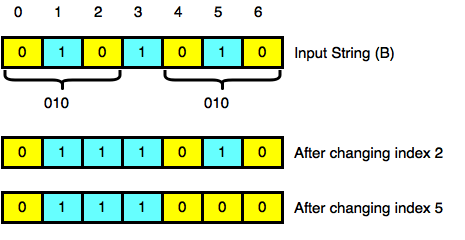
Binary String Comparison
- Definition: Binary string comparison measures the difference between two equal-length binary strings by counting the number of bit positions where they differ.
- Hamming Distance: The most common metric used is the Hamming Distance, which quantifies the number of mismatched bits.
- Equal Length Requirement: Both binary strings must be of the same length to perform a valid comparison.
- Applications: Used in error detection, cryptography, and data integrity checks.
- Bitwise Operations: Often implemented efficiently using bitwise XOR operations followed by counting set bits.
- Similarity Measure: A smaller Hamming Distance indicates higher similarity between two binary strings Lambda Expression .
- Performance: Ideal for fast comparison of binary data in networking, coding theory, and hardware design.
Applications in Error Detection
One of the most important uses of Hamming Distance is in error detection and correction. When data is transmitted over a noisy communication channel, it may get altered. To combat this, extra bits (redundancy) are added to the original data. The receiver can use the Hamming Distance between received data and valid codewords to detect and sometimes correct errors. For instance, if a code has a minimum Hamming Distance of 3, it can detect up to 2-bit errors and correct 1-bit errors. This concept underpins many coding schemes like Hamming codes, CRC (Cyclic Redundancy Check), and ECC (Error Correcting Codes). Hamming Distance plays a crucial role in the field of error detection and correction, particularly in digital communication systems. When data is transmitted over noisy channels, errors can occur, causing bits to flip from 0 to 1 or vice versa React Hooks . To ensure data integrity, systems need mechanisms to detect and correct these errors, and this is where Hamming Distance becomes essential. In error detection, a codeword, a sequence of bits with added redundancy is sent instead of raw data. The receiver compares the received codeword with the set of valid codewords. The Hamming Distance measures how many bits differ between the received word and each valid codeword. If the distance is zero, no error has occurred; if it is small, the receiver can identify the closest valid codeword and correct the error. For example, Hamming codes are a type of error-correcting code that uses the concept of Hamming Distance to detect and fix single-bit errors automatically. The minimum Hamming Distance between any two valid codewords determines the error detection and correction capability. A larger minimum distance allows detection and correction of more errors. Overall, Hamming Distance provides a mathematical foundation for designing robust communication protocols that maintain data accuracy, even in the presence of noise or interference.
Gain Your Master’s Certification in Full Stack Developer by Enrolling in Our Full Stack Master Program Training Course Now!
Hamming Code Basics
- Purpose: Hamming Code is an error-detecting and error-correcting code used to detect and correct single-bit errors in transmitted data.
- Redundancy Bits: It adds extra parity (redundancy) bits at specific positions in the data to enable error detection and correction.
- Positioning of Parity Bits: Parity bits are placed at positions that are powers of two (1, 2, 4, 8, …).
- Parity Check: Each parity bit checks a specific set of bits in the codeword to ensure even or odd parity Full Stack Training.
- Error Detection: When received, parity bits are checked; if any parity check fails, the position of the error can be identified.
- Single-Bit Correction: The position of the incorrect bit is found by combining the parity check results, allowing automatic correction.
- Use Cases: Widely used in computer memory (ECC RAM), digital communication, and data storage to improve reliability.
Implementing Hamming Distance in Python/C++
Hamming Distance is simple to implement programmatically. Linux Operating System Below is a basic Python implementation:
- def hamming_distance(s1, s2):
- if len(s1) != len(s2):
- raise ValueError(“Strings must be of equal length”)
- return sum(c1 != c2 for c1, c2 in zip(s1, s2))
In C++, the implementation might look like:
- int hammingDistance(string s1, string s2) {
- if (s1.length() != s2.length()) throw invalid_argument(“Strings must be of equal length”);
- int count = 0;
- for (int i = 0; i < s1.length(); ++i) {
- if (s1[i] != s2[i]) count++;
- }
- return count;
- }
These implementations can be optimized further, especially for binary strings, using bitwise operations.
Are You Preparing for Full Stack Jobs? Check Out ACTE’s Full stack Interview Questions and Answers to Boost Your Preparation!
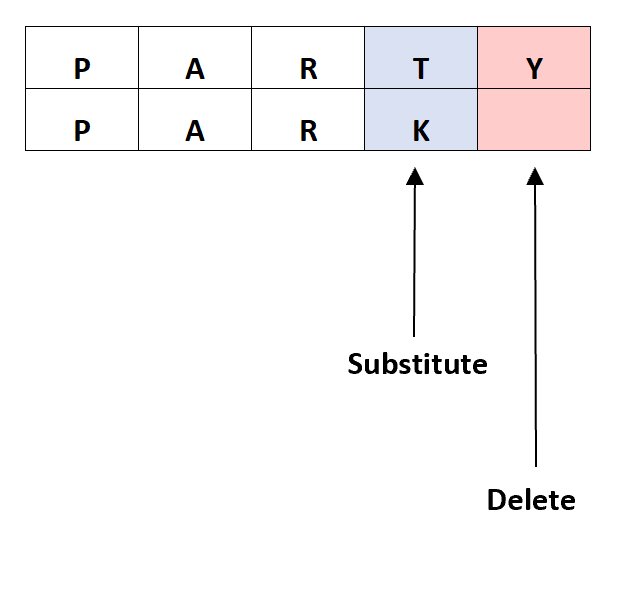
Differences from Levenshtein Distance
- Hamming counts differing positions between equal-length strings; Levenshtein counts edits between any-length strings.
- Hamming requires strings to be the same length; Levenshtein works with different lengths.
- Hamming counts only substitutions; Levenshtein counts insertions, deletions, and substitutions.
- Hamming is used in error correction for fixed-length data; Pointers in C Levenshtein is used in text and sequence analysis.
- Hamming is simpler and faster to compute; Levenshtein requires more complex algorithms like dynamic programming.
- Hamming outputs the number of differing positions; Levenshtein outputs the minimum edit operations needed.
- Hamming is undefined for unequal-length strings; Levenshtein handles length differences naturally.
Bit Manipulation for Hamming Calculation
When comparing binary numbers, Hamming Distance can be efficiently calculated using bitwise XOR. XOR (^) of two bits returns 1 StringBuilder if they are different and 0 if they are the same. Thus, counting the number of 1’s in the result gives the Hamming Distance.
In Python:
- def hamming_distance_bits(x, y):
- return bin(x ^ y).count(‘1’)
In C++:
- int hammingDistanceBits(int x, int y) {
- return __builtin_popcount(x ^ y);
- }
This bit manipulation technique is highly efficient and commonly used in performance-sensitive applications.
Conclusion
Hamming Distance is a foundational concept in data comparison, widely used in error detection, information theory, bioinformatics, and machine learning. It provides a simple, efficient way to quantify how similar or different two strings of equal length are. While limited in some respects (e.g., fixed-length requirement), its speed and simplicity make it a valuable tool in many real-world scenarios. Understanding how to implement and optimize Hamming Distance is essential for developers and data scientists working with binary data, Full Stack Training classification tasks, and system reliability. Both Hamming Distance and Levenshtein Distance are valuable metrics for measuring differences between strings, but they serve different purposes. Hamming Distance is ideal for comparing equal-length strings with simple substitutions, making it efficient for error detection in fixed-length data. In contrast, Levenshtein Distance is more flexible, handling insertions, deletions, and substitutions across strings of varying lengths, which suits applications like spell checking and DNA sequence analysis. Choosing the right distance measure depends on the nature of your data and the type of differences you need to capture.





