Dynamic Programming Explained: Concepts, Examples, and Applications

Introduction to Dynamic Programming

Dynamic Programming (DP) is a powerful algorithmic paradigm used to solve optimization problems by breaking them into simpler subproblems and solving each subproblem only once. The fundamental idea is to store the results of these subproblems to avoid redundant computations. This technique is especially useful for problems exhibiting Full Stack Training overlapping subproblems and optimal substructure properties. Unlike brute force approaches, which may recompute the same solution multiple times, dynamic programming ensures efficiency by remembering past results. It is frequently used in areas like operations research, economics, computer science, and bioinformatics. Problems that require decision making, resource allocation, or sequence alignment often rely on DP solutions. Dynamic Programming (DP) is a powerful algorithmic technique used to solve complex problems by breaking them down into simpler overlapping subproblems. Instead of solving the same subproblems repeatedly, DP solves each subproblem once and stores the result, typically in a table, to avoid redundant computations. This approach significantly improves efficiency, especially in problems with optimal substructure and overlapping subproblems. DP is widely applied in various fields such as computer science, economics, and bioinformatics, helping solve problems like shortest path,Data Structures & Algorithms sequence alignment, and resource allocation. The technique relies on two main strategies: memoization, which is a top-down approach that stores the results of recursive calls, and tabulation, a bottom-up approach that builds solutions iteratively. Classic examples of dynamic programming problems include calculating Fibonacci numbers, finding the longest common subsequence between sequences, and solving the knapsack problem. These problems share characteristics that make DP suitable: they can be divided into smaller, manageable subproblems, and the solution to the overall problem depends on solutions to these subproblems. Understanding dynamic programming equips programmers with a method to design efficient algorithms for a wide range of problems, making it a fundamental concept in algorithm design and competitive programming.

Interested in Obtaining Your Full stack Certificate? View The Full Stack Developer Course Offered By ACTE Right Now!

Characteristics of DP Problems

• Optimal Substructure: The optimal solution to the problem can be constructed from optimal solutions of its subproblems.
• Overlapping Subproblems: The problem can be broken down into subproblems which are solved multiple times.
• Recursive Structure: The problem can be defined recursively in terms of smaller subproblems.
• Memoization or Tabulation: Solutions to subproblems are stored to avoid redundant computations Call a Function in Python.
• Deterministic Results: Each subproblem has a deterministic, well-defined solution.
• Finite Subproblems: The number of distinct subproblems is finite and manageable.
• Non-Greedy Approach: DP problems generally require considering all possible subproblems, unlike greedy algorithms which make locally optimal choices.
• Complexity Reduction: DP reduces exponential time complexity problems into polynomial time by avoiding recomputation.

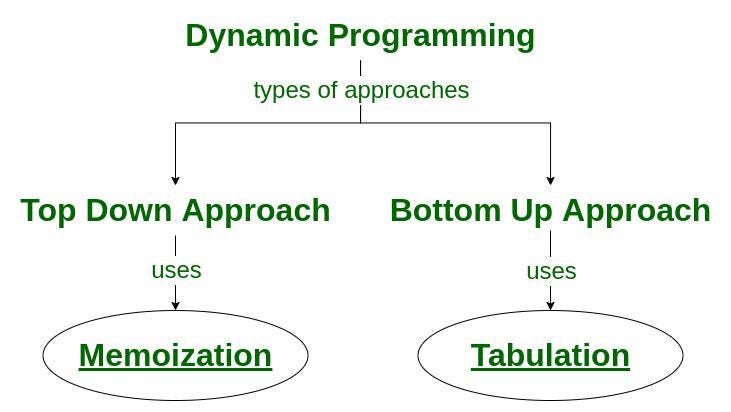
Memoization vs Tabulation

Memoization and Tabulation are two common techniques used in dynamic programming to optimize recursive problems by storing intermediate results.

• Memoization is a top-down approach: It starts with the original problem and breaks it down into subproblems recursively. Whenever a subproblem is solved, its result is stored (cached) in a data structure (usually an array or hash map). If the same subproblem is encountered again, Best Software Development Courses the stored result is returned immediately without recomputation. Memoization is easier to implement if you already have a recursive solution.



• Tabulation is a bottom-up approach It solves all the smaller subproblems first, typically by filling up a table (like an array) iteratively. Once the smaller subproblems are solved, larger subproblems are solved using these stored results. Tabulation usually requires careful ordering of computations but avoids the overhead of recursive calls.

Subscribe To Contact Course Advisor

Subscribe

Fibonacci Example

A classic example to illustrate dynamic programming is computing the nth Fibonacci number. The naive recursive solution has exponential time complexity because it recalculates the same values multiple times. Using DP, this can be optimized significantly. With memoization, we store the results of computed Fibonacci numbers in an array or dictionary and use them when needed. In tabulation, Full Stack Training we build the array from the base cases (e.g., F(0) = 0, F(1) = 1) and compute each subsequent Fibonacci number iteratively. This reduces the time complexity to O(n) and improves performance drastically.

Gain Your Master’s Certification in Full Stack Developer by Enrolling in Our Full Stack Master Program Training Course Now!

Longest Common Subsequence

• Definition: LCS is the longest sequence that appears in the same relative order, but not necessarily contiguously, in two sequences.
• Optimal Substructure: The LCS of two sequences can be built from the LCS of their prefixes.
• Overlapping Subproblems: LCS calculations for different prefixes overlap and can be reused Exploring Software Engineering.
• Dynamic Programming Solution: Uses a 2D table to store lengths of LCS for subproblems.
• State Definition: dp[i][j] represents the length of LCS of the first i characters of sequence 1 and first j characters of sequence 2.
• Recurrence Relation:
  1. If characters match: dp[i][j] = dp[i-1][j-1] + 1
  2. Else: dp[i][j] = max(dp[i-1][j], dp[i][j-1])
• Time Complexity: O(m * n), where m and n are the lengths of the two sequences. Applications: Used in diff tools, bioinformatics (DNA sequence analysis), and version control systems.

Develop Your Skills with Full stack Developer Certification Course

Weekday / Weekend BatchesSee Batch Details

Knapsack Problem

The 0/1 Knapsack Problem involves selecting a subset of items with given weights and values to maximize total value without exceeding the weight limit. It’s a typical optimization problem that fits well with the dynamic programming paradigm. A DP table is used where dp[i][w] represents the maximum value that can be obtained using the first i items and a knapsack capacity of w. Each entry is computed based on whether the ith item is included or excluded. The final answer is found at dp[n][W], StringBuilder where n is the number of items and W is the weight capacity.

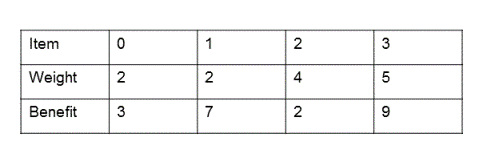
This solution operates in O(n*W) time complexity. The Knapsack Problem is a classic optimization challenge where you must maximize the total value of items placed in a knapsack without exceeding its weight capacity. Each item has a specific weight and value. The most common version, the 0/1 Knapsack, allows either taking an item whole or leaving it. Dynamic Programming solves this by building a table that stores the maximum value achievable for every weight limit up to the knapsack’s capacity. It uses the principle of optimal substructure, deciding for each item whether to include it based on maximizing total value. This approach efficiently finds the optimal solution.

Are You Preparing for Full Stack Jobs? Check Out ACTE’s Full stack Interview Questions and Answers to Boost Your Preparation!

Optimal Substructure

• Definition: A problem exhibits optimal substructure if an optimal solution can be constructed from optimal solutions of its subproblems.
• Key to DP: It is a fundamental property that enables dynamic programming solutions.
• Divide and Conquer: Problems with optimal substructure can be broken down into smaller overlapping subproblems.
• Example: In the shortest path problem, the shortest path from A to C via B consists of the shortest path from A to B plus the shortest path from B to C Linux Operating System.
• Solution Reuse: Optimal solutions to subproblems are combined to form the overall optimal solution.
• Not Always Present: Some problems lack this property and cannot be solved efficiently with DP.
• Greedy vs DP: Both approaches rely on optimal substructure, but greedy algorithms make locally optimal choices while DP considers all subproblems.
• Verification: To apply DP, verify if the problem has optimal substructure before proceeding.

State Transition Diagrams

State transition diagrams visually represent the transitions between various states in a dynamic programming problem. Each node in the diagram corresponds to a state, and the edges represent transitions based on decisions or changes in parameters. These diagrams help in understanding the flow of the DP solution and can be invaluable when designing the recurrence relation. They are particularly useful in complex problems like game theory models or multi-stage decision problems, where numerous states and transitions exist.State Transition Diagrams are graphical representations used to model the behavior of systems Break and Continue In C by depicting different states and the transitions between them. Each state represents a particular condition or situation in which a system can exist, while transitions indicate how the system moves from one state to another based on events or conditions. These diagrams are especially useful in computer science and engineering for designing and understanding finite state machines, control systems, and algorithms such as dynamic programming. In the context of dynamic programming, state transition diagrams help visualize how subproblems (states) relate to each other through transitions, which represent the choices or decisions leading from one subproblem to another. For example, in the knapsack problem, each state can represent a specific combination of items considered and the remaining capacity, while transitions correspond to including or excluding an item.

Full Stack Development Sample Resumes! Download & Edit, Get Noticed by Top Employers! Download

Conclusion

Dynamic programming is an essential tool in the toolkit of computer scientists and engineers. Its ability to simplify and optimize complex problems makes it invaluable in both academic and industry settings. By understanding the core principles of overlapping subproblems, optimal substructure, memoization, and tabulation and applying them through structured practice, one can unlock solutions Full Stack Training to some of the most challenging algorithmic problems. From classic examples like Fibonacci and LCS to complex real-world scenarios, mastering DP equips individuals with the analytical mindset needed to solve large-scale optimization tasks effectively and efficiently.