
- What is Recursion in Data Structures?
- Base Case and Recursive Case
- Direct vs Indirect Recursion
- Stack Frame and Memory
- Recursion Tree Visualization
- Factorial and Fibonacci
- Tail Recursion
- Recursion vs Iteration
- When Not to Use Recursion
- Practice Problems
- Debugging Recursive Code
- Summary
What is Recursion in Data Structures?
Recursion is a technique in which a function makes one or more calls to itself to solve a problem. Each recursive call simplifies the problem, moving it closer to a base case, which is a condition where the function no longer makes recursive calls. When the base case is reached, the function begins to return values and resolve all previous calls. The elegance of recursion lies in its ability to express complex logic with relatively simple and concise code.
- It refers to a method where the solution to a problem depends on solutions to smaller instances of the same problem, which is a key concept in Full Stack Training . In full-stack development, this idea can be applied to break down complex applications into smaller, manageable components, allowing developers to build both frontend and backend solutions in a modular, scalable way.
- This technique is particularly effective in scenarios like tree traversal, graph traversal, backtracking, and divide-and-conquer algorithms. However, mastering recursion requires an understanding of how it works internally, especially how the system stack handles recursive calls.
Recursion in data structures, recursion is a potent technique where a function calls itself to resolve smaller problems. It is essential to algorithms like sorting, searching, and tree traversals.
Would You Like to Get Your Complete Stack Certification?? View The Full Stack Developer Course Offered By ACTE Right Now!
Base Case and Recursive Case
- Base Case: This is the simplest instance of the problem and serves as the stopping condition. Without a base case, recursion would continue indefinitely.
- Recursive Case: This is the part of the function where it calls itself with modified parameters to move toward the base case.
- Base Case: factorial(0) = 1
- Recursive Case: factorial(n) = n * factorial(n – 1)
- Direct Recursion: When a function directly calls itself.
- Indirect Recursion: When a function calls another function that eventually calls the first function.
- Factorial: Defined as n! = n × (n – 1)!, with factorial(0) = 1 as the base case. This is a linear recursion problem.
- Fibonacci Sequence: Defined as F(n) = F(n – 1) + F(n – 2), with base cases F(0) = 0 and F(1) = 1. The naive recursive implementation results in exponential time complexity due to repeated subproblem computation.
- Recursion is cleaner and often aligns closely with the mathematical definition of a problem. It is preferred in scenarios like tree traversal, graph traversal, and solving problems with divide-and-conquer strategies.
- Iteration is generally more efficient in terms of memory usage and speed, particularly in languages that don’t support tail call optimization.
- When the recursion depth could be very large, leading to a stack overflow.
- When an iterative approach is simpler and more efficient.
- When the environment doesn’t optimize for tail calls and memory is a constraint.
- Use Print Statements: Print the function parameters before each call to trace execution.
- Visualize the Call Stack: Understand how the recursive calls build and resolve.
- Test Base Cases: Ensure the base case is correct and reachable.
- Use Small Inputs: Begin testing with small input sizes to avoid overwhelming the stack and to trace logic easily.
- Debugging Tools: Utilize IDE features like breakpoints and call stack viewers to step through the recursive logic.
If the base case is incorrectly defined or omitted, the function will result in a stack overflow error due to infinite recursive calls.
Direct vs Indirect Recursion
Designing effective algorithms requires an understanding of both direct and indirect recursion in data structures. Recursion comes in two primary types: each with unique implications for control flow and memory usage. To master these concepts, it’s important to grasp the foundational differences outlined in Coding vs Programming a guide that clarifies how algorithmic thinking, abstraction, and implementation diverge across development disciplines.
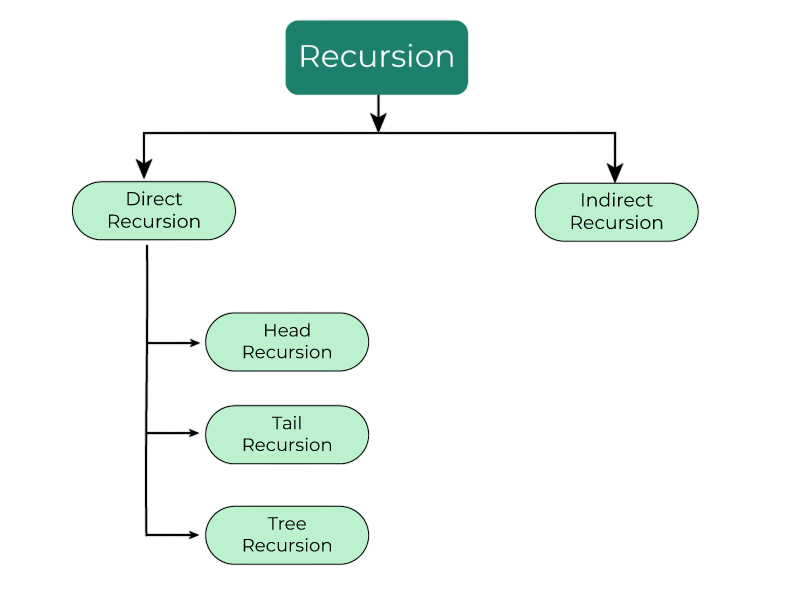
Direct recursion is straightforward and easier to trace and debug. Indirect recursion is typically used in mutually recursive functions, where two or more functions depend on each other to complete a task.Functions calling themselves directly or through other functions is a component of both direct and indirect recursion in data structures, which influences the recursive solution of issues. Although less common, indirect recursion can be powerful when structured correctly.
Stack Frame and Memory
Each time a function is called, including recursive calls, the system allocates memory on the call stack in the form of a stack frame. This frame stores the function’s parameters, local variables, and return address. As recursion proceeds, new stack frames are pushed onto the stack. When the base case is reached and the function returns, the stack frames are popped off one by one. This mechanism explains why recursion can lead to stack overflow errors if the recursion depth is too great. To navigate such challenges and build a strong foundation in computational thinking, How to Become a Programmer offers essential To prevent this, recursive functions should be designed to minimize depth and avoid unnecessary calls. Understanding how the stack works helps in writing optimized recursive solutions and debugging them effectively.
Recursion Tree Visualization
A recursion tree is a diagram that helps visualize the flow of recursive calls. Each node in the tree represents a function call, and the branches represent the recursive calls made by that function. This tool is invaluable in understanding the structure and cost of recursive algorithms. To connect such algorithmic analysis with broader project planning, What Are SDLC Phases offers a structured view mapping how design, development, and testing stages align with computational logic and performance evaluation.
Enroll in Our Program to Obtain Your Master’s Certification in Full Stack Development Full Stack Master Program Training Course Now!
Factorial and Fibonacci
Two classic problems often solved using recursion are:
The Fibonacci example highlights one of the downsides of naive recursion: redundancy and inefficiency. This can be resolved by applying dynamic programming techniques like memoization or tabulation. In Full Stack Training learners not only explore such algorithmic optimizations but also learn how to apply similar principles in backend development to improve the performance of web applications, especially when working with data-heavy processes or APIs.
Recursion vs Iteration
While recursion provides elegant and concise solutions, it comes with trade-offs when compared to iteration: including stack depth limitations and performance overhead in certain scenarios. For tasks that require constant-time access and efficient data retrieval, understanding the Python Hash Table is crucial it offers a powerful alternative through key-value mapping, enabling fast lookups and optimized memory usage in iterative algorithms.
Converting recursive solutions to iterative ones often involves the use of stacks or queues to simulate the recursive behavior explicitly.
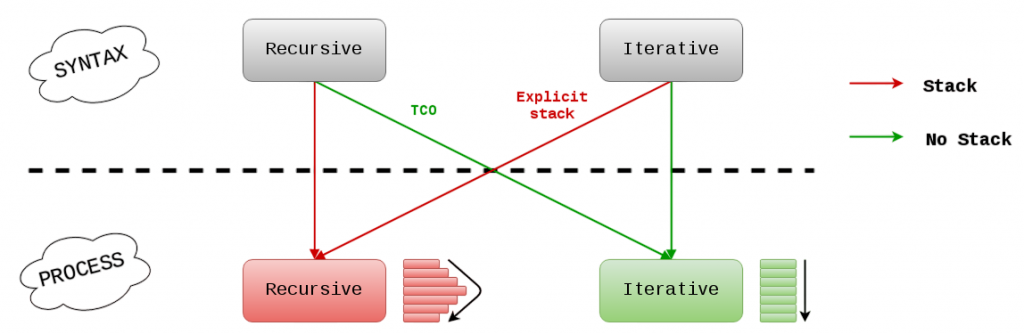
Converting recursive solutions to iterative ones often involves the use of stacks or queues to simulate the recursive behavior explicitly.
Are You Preparing for Full Stack Developer Jobs? Check Out ACTE’s Full Stack Interview Questions and Answers to Boost Your Preparation!
When Not to Use Recursion
Despite its advantages, recursion is not always the ideal choice. Avoid recursion in the following cases:
Always evaluate whether the recursive approach adds clarity and efficiency or complicates the problem.
Debugging Recursive Code
Debugging recursive code is made easier by using print statements or a debugger, which can trace the flow and spot improper base or recursive situations. Multiple function calls and stack traces make debugging recursive code difficult. Debugging recursive functions can be tricky due to the multiple layers of function calls. To manage such complexity in concurrent environments, understanding What Is a Thread in Java is essential it introduces the concept of lightweight processes that run independently, helping developers isolate logic, improve performance, and streamline debugging across parallel executions.
Mastering debugging techniques will lead to greater confidence in implementing and testing recursive solutions.
Summary
Recursion is a powerful concept that enables elegant solutions to problems that are inherently recursive in nature. By mastering base and recursive cases, understanding stack memory usage, and visualizing recursion trees, developers can write effective recursive algorithms. Although recursion may introduce performance and memory overhead, its clarity and alignment with mathematical models often justify its use. In Full Stack Training students learn to balance the use of recursion with performance considerations, applying best practices in both front-end and back-end development to optimize code while maintaining readability and structure. Recognizing when to use recursion versus iteration, and how to optimize recursive solutions through techniques like memoization or tail recursion, is key to becoming a proficient programmer. With practice, recursion becomes an indispensable tool in the problem solver’s toolkit.




