
- Introduction to Fibonacci Sequence
- Formula and Logic
- Iterative Implementation in C
- Recursive Implementation in C
- Memory and Time Complexity
- Edge Cases
- Applications of Fibonacci
- Conclusion
Introduction to Fibonacci Sequence
The Fibonacci sequence is one of the most iconic number patterns in mathematics and computer science. It starts with two initial numbers, typically 0 and 1, and every subsequent number is the sum of the previous two. Mathematically, this can be expressed as F(n) = F(n-1) + F(n-2), where F(0) = 0 and F(1) = 1. The sequence grows quickly: 0, 1, 1, 2, 3, 5, 8, 13, 21, 34, and so forth. The Fibonacci sequence is widely studied because of its simple definition, rich mathematical properties, and broad applications, from computer algorithms to nature’s patterns, such as spirals in sunflowers and pinecones. For programmers Cloud Computing Training , especially those working in C, it’s an excellent example to learn about loops, recursion, time complexity, and optimization techniques. The Fibonacci Sequence is a series of numbers where each number is the sum of the two preceding ones, starting from 0 and 1. It begins as 0, 1, 1, 2, 3, 5, 8, and so on. This sequence is named after Leonardo of Pisa, known as Fibonacci, who introduced it to Western mathematics in the 13th century. The Fibonacci Sequence appears in various natural phenomena such as the arrangement of leaves, flower petals, and shell spirals. It also has applications in computer algorithms, mathematics, and financial modeling due to its unique recursive properties.
To Earn Your Cloud Computing Course Certification, Gain Insights From Leading Cloud Computing Experts And Advance Your Career With ACTE’s Cloud Computing Course Today!
Formula and Logic
The logic behind the Fibonacci sequence is straightforward: each number is derived from adding the previous two. The recursive nature of this definition makes it a great example for understanding recursion in programming. Reverse a String The base conditions are:
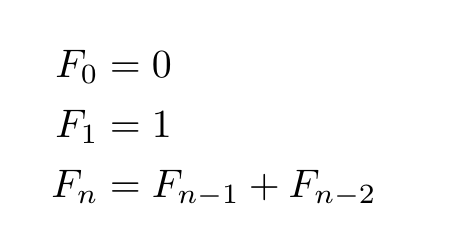
Beyond these, each F(n) is calculated by adding F(n-1) and F(n-2). In C programming, this recursive logic translates directly into code but can also be implemented iteratively, which is more efficient. Understanding this core formula is critical, as it forms the backbone for different implementations, whether it’s for generating sequences, solving dynamic programming problems, or modeling real-world systems.
Iterative Implementation in C
The iterative method is a straightforward and efficient way to compute Fibonacci numbers. It avoids the overhead of recursive function calls and uses simple loops and temporary Lambda Expression Iterative Implementation in C The iterative method is a straightforward and efficient way to compute Fibonacci numbers. variables to keep track of the last two computed values. Here’s how it looks in C: #include void printFibonacci(int n) { int t1 = 0, t2 = 1, nextTerm; printf(“Fibonacci Series: %d, %d, “, t1, t2); for (int i = 3; i <= n; ++i) { nextTerm = t1 + t2; printf("%d, ", nextTerm); t1 = t2; t2 = nextTerm; } printf("\n"); } int main() { int n; printf("Enter the number of terms: "); scanf("%d", &n); printFibonacci(n); return 0; } This method has a time complexity of O(n) and space complexity of O(1), making it suitable for most practical applications. It’s also beginner-friendly and widely used in interviews.variables to keep track of the last two computed values. Here’s how it looks in C:
- #include
- void printFibonacci(int n) {
- int t1 = 0, t2 = 1, nextTerm;
- printf(“Fibonacci Series: %d, %d, “, t1, t2);
- for (int i = 3; i <= n; ++i) {
- nextTerm = t1 + t2;
- printf(“%d, “, nextTerm);
- t1 = t2;
- t2 = nextTerm;
- }
- printf(“\n”);
- }
- int main() {
- int n;
- printf(“Enter the number of terms: “);
- scanf(“%d”, &n);
- printFibonacci(n);
- return 0;
- }
This method has a time complexity of O(n) and space complexity of O(1), making it suitable for most practical applications. It’s also beginner-friendly and widely used in interviews.
Would You Like to Know More About Cloud Computing Course? Sign Up For Our Cloud Computing Course Now!
Recursive Implementation in C
The recursive method aligns closely with the mathematical definition of Fibonacci. It’s a great way to introduce recursion, but it comes with a performance cost. Each call to the function triggers two Prim’s Algorithm Explanation more calls unless it hits the base case. Here is a basic recursive approach:
- #include
- int fibonacci(int n) {
- if (n == 0)
- return 0;
- else if (n == 1)
- return 1;
- else
- return fibonacci(n-1) + fibonacci(n-2);
- }
- int main() {
- int n;
- printf(“Enter the number of terms: “);
- scanf(“%d”, &n);
- printf(“Fibonacci Series: “);
- for (int i = 0; i < n; i++) {
- printf(“%d, “, fibonacci(i));
- }
- printf(“\n”);
- return 0;
- }
While elegant, this approach has a time complexity of O(2^n), making it impractical for large input values. It’s an excellent learning tool, though, for understanding recursion and call stacks.
Memory and Time Complexity
Understanding Memory and Time Complexity is crucial for Cloud Computing Training choosing the right approach. The iterative method has:
- Time Complexity: O(n)
- Space Complexity: O(1)
- Time Complexity: O(2^n)
- Space Complexity: O(n) (due to function call stack)
- n = 0: Should return an empty output or just 0.
- n = 1: Output should be 0 (or 0, 1 depending on interpretation).
- Negative Input: Should be flagged as invalid.
- Algorithm Design: Used in divide-and-conquer techniques.
- Financial Markets: Fibonacci retracement levels are used in technical analysis.
- Nature: Patterns in flowers, pinecones, and PPC Analyst Salary shells.
- Art & Architecture: The Golden Ratio, derived from Fibonacci numbers, influences design.
- Computer Graphics: Procedural generation of natural scenes. These wide-ranging applications highlight its importance and relevance across disciplines.
In contrast, the recursive version has:
Memoization, a dynamic programming technique, significantly reduces the time complexity of the recursive method by storing the Fibonacci Series in Python results of expensive function calls and reusing them.
Gain Your Master’s Certification in Cloud Computing by Enrolling in Our Cloud Computing Master Program Training Course Now!
Edge Cases
Robust code handles all input scenarios. For Fibonacci series generation:
A simple input check before proceeding with Kruskal Algorithm in DAA calculations ensures the program behaves predictably under all circumstances.
Are You Interested in Learning More About Cloud Computing Course? Sign Up For Our Cloud Computing Course Today!
Applications of Fibonacci
The Fibonacci sequence is more than an academic curiosity. It has real-world applications, such as:
Preparing for Cloud Computing Job Interviews? Have a Look at Our Blog on Cloud Computing Interview Questions and Answers To Ace Your Interview!
Conclusion
The Fibonacci series is not only a mathematical concept but also a crucial learning tool in programming. In C, it offers insight into different control structures, recursion, optimization, and dynamic programming. Through iterative and recursive implementations, programmers can gain a deeper understanding Cloud Computing Training of algorithm design and performance trade-offs. Its relevance in real-world applications from art to finance makes it a vital topic in both academic and professional environments. Whether you’re writing simple loops or building efficient algorithms, mastering the Fibonacci sequence is an excellent step in becoming a proficient C programmer.





