
- Introduction to Greedy Algorithms
- Greedy vs Dynamic Programming
- Design Paradigm of Greedy Approach
- Greedy Algorithm Properties
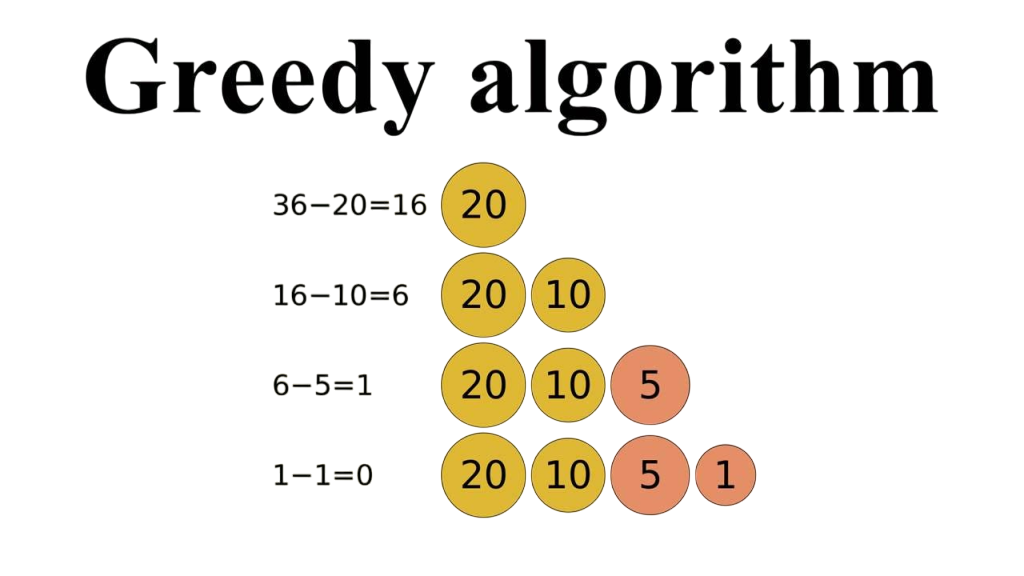
- Classic Examples (e.g., Activity Selection, Coin Change)
- Huffman Encoding with Greedy
- Job Sequencing Problem
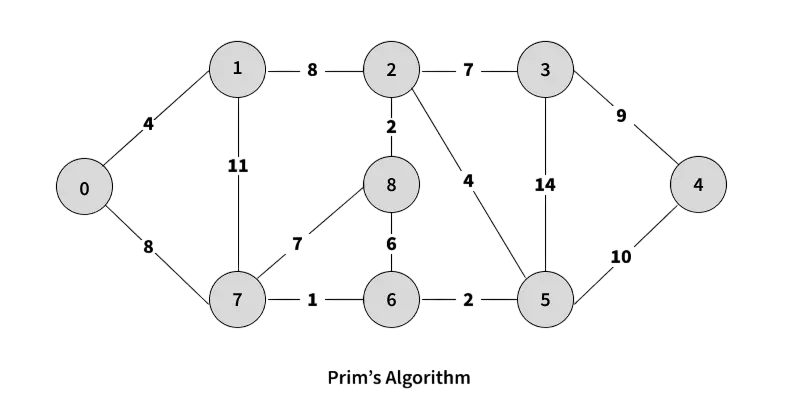
- Greedy Algorithm in Graphs (Prim’s, Kruskal’s)
- Conclusion
Introduction to Greedy Algorithms
A Greedy Algorithm is a problem-solving paradigm that builds up a solution piece by piece, always choosing the next piece that offers the most immediate benefit or “greedy” choice. It works by making local optimum decisions at each step with the hope that these choices will lead to a global optimum solution. This method is often used in optimization problems where the goal is to maximize or minimize some value (e.g., shortest path, largest profit). Greedy algorithms are known for their simplicity, efficiency, and ease of implementation, but they do not always produce the optimal solution for all problems. Greedy algorithms are a class of algorithms used for solving optimization problems by making a series of choices, each of which looks the best at the moment. The fundamental idea behind greedy algorithms is to build up a solution piece by piece Python Training, always selecting the option that offers the most immediate benefit without worrying about the consequences for future steps. This approach contrasts with other methods, such as dynamic programming or backtracking, which consider the global problem more holistically. Greedy algorithms are popular because they are usually simple to design and implement, often providing efficient solutions with relatively low time complexity. However, they do not always guarantee the optimal solution for every problem. Their success depends on the problem having the “greedy-choice property” meaning that a locally optimal choice leads to a globally optimal solution and “optimal substructure” meaning the problem can be broken down into smaller subproblems with optimal solutions. Common examples of problems solved by greedy algorithms include finding the minimum spanning tree in a graph Python Developer Skills (using Prim’s or Kruskal’s algorithm), the activity selection problem, and the coin change problem for certain coin systems. When applicable, greedy algorithms offer a fast and effective approach to complex problems, making them an essential tool in computer science and operations research.
Interested in Obtaining Your Python Certificate? View The Python Developer Course Offered By ACTE Right Now!
Greedy vs Dynamic Programming
Greedy
- Simple and Intuitive: Greedy algorithms make the best immediate choice at each step, making them easy to understand and implement.
- Local Optimization: They focus on optimizing locally without reconsidering past decisions.
- Optimal Solutions in Specific Cases: Work well when problems have the greedy-choice property and optimal substructure.
- Efficient and Fast: Typically faster with lower time complexity compared to other methods like dynamic programming Minimum Spanning Tree.
- Limitations: Not suitable for every problem; may produce suboptimal results if the problem structure doesn’t support greedy choices.
- Common Examples: Includes algorithms like Prim’s algorithm, Kruskal’s algorithm, activity selection, and certain coin change problems.
- Ideal Use Cases: Often used for resource allocation, scheduling, and network design when the problem conditions fit.
- Breaks Problems into Subproblems: Solves complex problems by dividing them into smaller, overlapping subproblems.
- Stores Intermediate Results: Uses memoization or tabulation to save subproblem solutions, avoiding redundant calculations.
- Guarantees Optimal Solutions: Provides optimal results for problems with the optimal substructure property.
- Considers All Possible Solutions: GUI Tkinter Module Examines multiple paths and combines results to find the best overall solution.
- More Complex and Resource-Intensive: Generally requires more time and memory than greedy algorithms due to solving many subproblems.
- Widely Applicable: Used for problems like the knapsack problem, shortest path algorithms, Fibonacci sequence, and sequence alignment.
- Useful for Overlapping Subproblems: Especially effective when the same subproblems appear multiple times in the problem space.
Dynamic :
Design Paradigm of Greedy Approach
The design paradigm of the greedy approach revolves around making a series of locally optimal choices with the goal of reaching a globally optimal solution. At each step, the algorithm selects the best possible option available without reconsidering previous decisions. This step-by-step method distinguishes greedy algorithms from other approaches like dynamic programming, which analyze all possible solutions more exhaustively. The success of the greedy approach depends on two critical properties: the greedy-choice property and optimal substructure. The greedy-choice property means that making the best local choice at each step Python Training will lead to the best overall solution. Optimal substructure means that the problem can be broken down into smaller subproblems, and the optimal solution to the larger problem incorporates optimal solutions to these subproblems. Because greedy algorithms do not revisit previous decisions or explore all possibilities, they tend to be faster and require less memory compared to more complex techniques. However, they do not guarantee an optimal solution for every problem. Greedy methods work best when the problem naturally fits these properties, such as in the case of minimum spanning trees, activity selection, or certain coin change problems. In such cases, the greedy design paradigm offers a simple, intuitive, and efficient way to solve optimization problems.
Greedy Algorithm Properties
- Greedy-Choice Property: A global optimal solution can be arrived at by choosing a local optimum at each step.
- Optimal Substructure: The problem can be broken down into smaller subproblems whose optimal solutions contribute to the overall solution.
- Irrevocable Decisions: Once a choice is made, it cannot be changed or revisited later in the algorithm.
- No Backtracking: Greedy algorithms do not reconsider previous choices, Reverse C++ Vector making them faster but sometimes less flexible.
- Feasibility: Every choice made must be feasible, i.e., it must satisfy the problem’s constraints.
- Local vs Global: Focuses on local optimization that leads to a globally optimal or near-optimal solution.
- Efficiency: Generally offers faster and simpler solutions compared to exhaustive search or dynamic programming.
- Sorting jobs by descending profit.
- Assigning jobs to the latest available slot before their deadline.
- This ensures that higher-profit jobs are given priority, and deadlines are respected, IPO Cycle yielding maximum total profit.
- Prim’s Algorithm: Builds a minimum spanning tree (MST) by adding the lowest weight edge that connects a vertex in the MST to a vertex outside it. It uses a priority queue (min-heap) and always picks the next lowest-cost edge.Prim’s algorithm is a classic greedy algorithm used to find the minimum spanning tree (MST) of a connected, weighted graph. The minimum spanning tree connects all the vertices together with the smallest possible total edge weight, without forming any cycles. Prim’s algorithm starts with an arbitrary vertex and grows the MST one edge at a time. At each step, it selects the smallest weight edge that connects a vertex already Throw and Throws Java in the MST to a vertex outside of it.
- Kruskal’s Algorithm: Sorts all edges by weight and adds them to the MST, provided they don’t form a cycle. It uses the greedy strategy of always choosing the lowest weight edge. Kruskal’s algorithm is a greedy method used to find the minimum spanning tree (MST) of a connected, weighted graph. Unlike Prim’s algorithm, which grows the MST from a single starting vertex, Kruskal’s algorithm builds the MST by sorting all the edges in the graph by their weight and then adding them one by one in ascending order. At each step, it adds the next smallest edge to the growing forest, as long as adding that edge does not create a cycle. This is typically checked using a data structure called a disjoint set union (DSU) or union-find to efficiently detect cycles.
- import unicode data
- s1 = “café”
- s2 = “café”
- print(s1 == s2)
- s1_nfc = unicodedata.normalize(‘NFC’, s1)
- s2_nfc = unicodedata.normalize(‘NFC’, s2)
- print(s1_nfc == s2_nfc)
Gain Your Master’s Certification in Python Developer by Enrolling in Our Python Master Program Training Course Now!
Classic Examples (e.g., Activity Selection, Coin Change)
Activity Selection Problem:
Given n activities with start and finish times, the goal is to select the maximum number of activities that don’t overlap. The greedy approach selects the activity that finishes earliest,Data Structures & Algorithms allowing more room for subsequent activities.
Coin Change Problem (Greedy):
Given a set of coin denominations and an amount, the goal is to minimize the number of coins used. A greedy algorithm works when the coin system is canonical (like US denominations), always picking the largest denomination that does not exceed the remaining amount. However, for arbitrary denominations, greedy may not produce the optimal result, making it unsuitable in such cases.
Huffman Encoding with Greedy
Huffman Coding is a classic application of greedy strategy used in data compression. It builds an optimal binary tree where frequently occurring characters have shorter codes. The algorithm uses a priority queue (min-heap) to iteratively combine the two lowest-frequency nodes until a Paging in Operating Systems complete Huffman Tree is formed. This greedy process ensures minimum average code length, which is ideal for compressing text or media files. Huffman coding is widely used in ZIP compression, JPEG, and MP3 file formats.
Are You Preparing for Python Jobs? Check Out ACTE’s Python Interview Questions and Answers to Boost Your Preparation!
Job Sequencing Problem
In the Job Sequencing Problem, we are given n jobs, each with a deadline and profit. Only one job can be scheduled at a time, and the aim is to schedule jobs to maximize total profit.
The greedy solution involves:
Greedy Algorithm in Graphs (Prim’s, Kruskal’s)
Greedy algorithms are especially powerful in graph algorithms. Two key examples are:
Handling Unicode Strings
Sorting Unicode strings works the same as sorting regular ASCII strings Complete Guide on System Software, but it’s important to normalize the text to avoid inconsistencies. For example:
Unicode normalization ensures that visually identical strings are treated as equal, which is crucial when sorting international text.
Conclusion
In summary, Greedy Algorithms offer a powerful yet simple method to solve many optimization problems. By making the most optimal local choice at each step, greedy approaches often find globally optimal solutions provided the problem exhibits the right properties Python Training (greedy-choice and optimal substructure). From graph theory and data compression to real-time systems and scheduling, greedy algorithms are vital tools in a programmer’s toolkit. However, it’s crucial to understand the problem characteristics before choosing a greedy strategy. In cases where greedy fails, techniques like dynamic programming or backtracking might be more suitable. As a best practice, always attempt to prove the correctness of your greedy approach before relying on it in critical applications.





