40+ [REAL-TIME] DAA Interview Questions and Answers

Last updated on 30th Apr 2024, Popular Course

DAA, or Design and Analysis of Algorithms, is a field in computer science concerned with the study of algorithms: their design, analysis, implementation, and application. It involves understanding various algorithmic techniques, such as divide and conquer, dynamic programming, greedy algorithms, and more, and analyzing their efficiency in terms of time and space complexity. The goal is to develop algorithms that solve computational problems effectively and efficiently.

1. What is an algorithm?

Ans:

An algorithm is a step-by-step procedure or set of rules used to solve a specific problem or perform a particular task. It’s a finite sequence of well-defined instructions that transforms input into output. They can range from simple calculations to complex processes used in artificial intelligence and data analysis. Essentially, they provide a systematic approach to solving problems and achieving desired outcomes efficiently and accurately.

2. What is the significance of analyzing algorithms?

Ans:

• Analyzing algorithms helps in understanding their efficiency in terms of time and space requirements.
• It allows us to compare different algorithms for the same problem and choose the most suitable one based on performance characteristics.
• This analysis is crucial for optimizing software performance, improving resource utilization, and ultimately enhancing user experience.

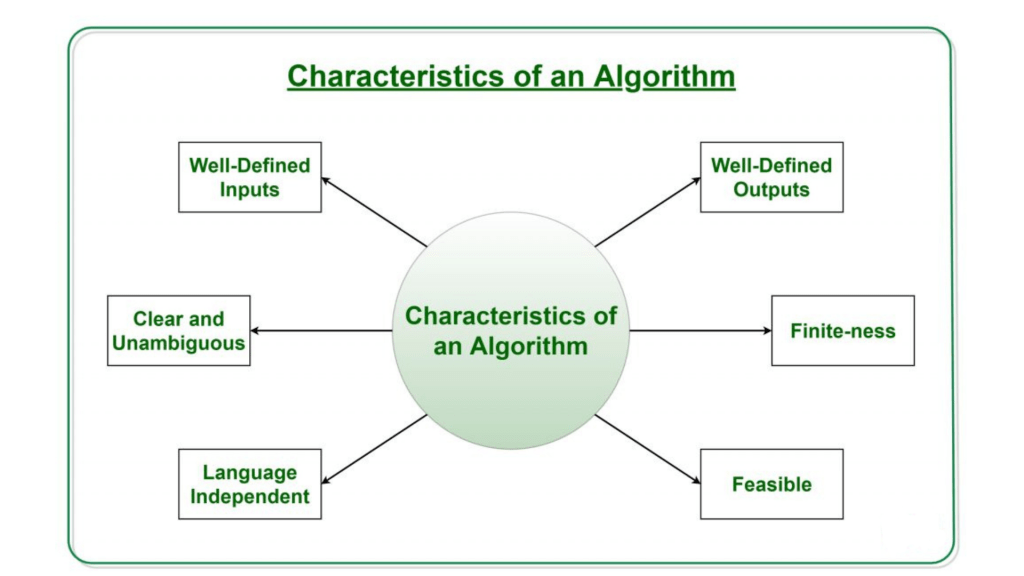
3. Explain the importance of time complexity in algorithm analysis.

Ans:

Time complexity measures the amount of time an algorithm takes to complete as a function of the size of its input. It’s crucial because it helps us predict how the algorithm will perform as the input size grows. By understanding the time complexity, we can choose the most efficient algorithm for a given problem.

4. What is space complexity, and why is it important?

Ans:

Space complexity measures the amount of memory an algorithm requires as a function of the size of its input. It’s essential because it helps us understand an algorithm’s memory usage, which is crucial, especially in resource-constrained environments like embedded systems or when dealing with large datasets.

5. What is the difference between worst-case, best-case, and average-case time complexity?

Ans:

Aspect	Worst-case Time Complexity	Best-case Time Complexity	Average-case Time Complexity
Definition	The longest time an algorithm can execute for any given size n input.	SThe shortest running time of an algorithm for any size n input.	The predicted running time of an algorithm, averaged over all size n input possibilities.
Representation	represented by \(O(f(n))\) where \(f(n)\) is an upper constraint on the algorithm’s execution time.	represented by \(Ω(g(n))\) where \(g(n)\) is a lower bound on the algorithm’s execution time./task	Usually expressed as the algorithm’s average time for all potential inputs of size n; this is frequently symbolized by (΃(h(n))\)./task
Significance	provides an upper constraint on the algorithm’s performance, ensuring that the algorithm won’t take longer than this to finish.	Sgives an indicator of the algorithm’s performance in the best-case scenario; nevertheless, it might not be indicative of common or real-world scenarios.	takes into account the anticipated time required across a variety of inputs to provide a more accurate assessment of the algorithm’s performance.
Example	Searching for an element in an unsorted list where the element is not present (e.g., linear search).	finding an element (e.g., linear search) in an unsorted list when the element is the first element.	Quicksort algorithm, where the average case occurs when the input is randomly distributed.

6. Explain the divide and conquer algorithm paradigm with an example.

Ans:

• Divide and conquer is a problem-solving technique where a problem is divided into smaller subproblems, solved recursively, and then combined to find the solution to the original problem.
• An example is the merge sort algorithm, where the array is divided into halves, sorted recursively, and then merged.

7. What is dynamic programming, and when is it used?

Ans:

Dynamic programming is a technique used to solve problems by breaking them down into simpler subproblems and solving each subproblem only once. It’s typically used when the problem exhibits overlapping subproblems and optimal substructure properties, such as in the case of the Fibonacci sequence or the knapsack problem.

8. Explain greedy algorithms and provide an example of their application.

Ans:

Greedy algorithms make locally optimal choices at each step in the hope of finding a global optimum. They’re used when a problem can be solved by making a series of optimal choices at the time. An example is the coin change problem, where the goal is to make change for a given amount using the fewest possible coins.

9. What is backtracking, and how is it different from brute force?

Ans:

• Backtracking is a technique for solving problems by exploring all possible solutions and eliminating those that do not satisfy the problem constraints.
• It differs from brute force in that it intelligently searches the solution space, pruning branches that cannot lead to a valid solution, which makes it more efficient than exhaustively trying every possible solution.

10. Explain the importance of algorithm design paradigms in problem-solving.

Ans:

Algorithm design paradigms provide structured approaches for solving different types of problems efficiently. By understanding and applying these paradigms, such as divide and conquer, dynamic programming, greedy algorithms, and backtracking, we can develop algorithms that are easier to understand, analyze, and implement, ultimately leading to more effective solutions to complex problems.

11. What are the main steps involved in designing an algorithm?

Ans:

The main steps in designing an algorithm include understanding the problem, determining the inputs and outputs, choosing appropriate data structures and algorithmic techniques, devising a plan or algorithm, implementing the algorithm, testing and debugging it, and finally, analyzing its efficiency.

12. Explain the concept of asymptotic analysis in algorithm analysis.

Ans:

Asymptotic analysis evaluates an algorithm’s performance as the input size approaches infinity. It focuses on the algorithm’s behaviour for large inputs and provides insights into how the algorithm scales. Common notations used in asymptotic analysis include Big O, Big Omega, and Big Theta, which describe the upper, lower, and tight bounds of an algorithm’s time or space complexity, respectively.

13. What are the different types of algorithm complexity?

Ans:

• The different types of algorithm complexity include time complexity, space complexity, and sometimes auxiliary space complexity.
• Time complexity measures the number of operations or steps an algorithm takes to complete as a function of the input size.
• Space complexity measures the amount of memory an algorithm uses as a function of the input size.
• Auxiliary space complexity accounts for the extra space used by the algorithm apart from the input space.

14. Explain the concept of recurrence relation in algorithm analysis.

Ans:

A recurrence relation is a mathematical equation that recursively defines a sequence or function in terms of its previous values. In algorithm analysis, recurrence relations are often used to describe the time complexity of recursive algorithms. Solving recurrence relations involves finding a closed-form solution that expresses the time complexity of the algorithm in terms of its input size.

15. What is the Master Theorem, and when is it used in algorithm analysis?

Ans:

The Master Theorem is a mathematical tool used to solve recurrence relations that arise in the analysis of divide-and-conquer algorithms. It provides a way to determine the time complexity of algorithms with a specific form of recurrence relation. The Master Theorem simplifies the process of analyzing the time complexity of algorithms like merge sort, binary search, and quicksort.

16. Explain the concept of amortized analysis in algorithm analysis.

Ans:

• Amortized analysis is a method for analyzing the average time or space complexity of a sequence of operations on a data structure.
• It considers the total cost of a series of operations divided by the number of operations, providing an average cost per operation.
• Amortized analysis is particularly useful for analyzing data structures with expensive individual operations but overall efficient performance, such as dynamic arrays or hash tables.

17. What are some common algorithmic techniques used to solve graph problems?

Ans:

Some common algorithmic techniques used to solve graph problems include depth-first search (DFS) and breadth-first search (BFS) for traversal and pathfinding, Dijkstra’s algorithm for single-source shortest paths, the Bellman-Ford algorithm for single-source shortest paths with negative weights, and the Floyd-Warshall algorithm for all pairs of shortest paths

18. Explain the concept of NP-completeness and its significance in algorithm analysis.

Ans:

NP-completeness is a class of problems for which no known efficient algorithm exists to solve them in polynomial time. A problem is considered NP-complete if every problem in the NP class can be reduced to it in polynomial time. The significance of NP-completeness lies in its implications for algorithm design. If a problem is NP-complete, finding an efficient solution is unlikely, and heuristic or approximation algorithms may be necessary.

19. What is the difference between a greedy algorithm and a dynamic programming algorithm?

Ans:

• Greedy algorithms make locally optimal choices at each step with the hope of finding a global optimum.
• In contrast, dynamic programming algorithms solve problems by breaking them down into simpler subproblems and solving each subproblem only once.
• The main difference lies in their approach to problem-solving: greedy algorithms make decisions based solely on the current state, while dynamic programming algorithms consider the entire problem space and optimize globally.

20. How do you determine the correctness of an algorithm?

Ans:

An algorithm’s correctness can be determined by analyzing its logic, verifying its compliance with the problem requirements, and testing it with various input cases, including boundary cases and edge cases. Additionally, mathematical proofs, such as loop invariants or induction, can be used to formally verify an algorithm’s correctness. Debugging techniques, such as step-by-step execution and code reviews, are also essential for identifying and fixing any errors or inconsistencies in the algorithm.

21. Explain the concept of a greedy choice property in greedy algorithms.

Ans:

The greedy choice property states that at each step of a greedy algorithm, the locally optimal choice leads to a globally optimal solution. In other words, a greedy algorithm makes the best possible choice at each step without considering the consequences of that choice on future steps. This property is crucial for the correctness of greedy algorithms and is often proven using mathematical induction or contradiction.

22. What is a dynamic programming table, and how is it used in dynamic programming algorithms?

Ans:

• A dynamic programming table is a data structure used to store intermediate results in dynamic programming algorithms.
• It typically has dimensions corresponding to the sizes of the input parameters and is filled in a bottom-up or top-down fashion with the solutions to subproblems.
• The table allows dynamic programming algorithms to avoid redundant computations by storing and reusing previously computed results, leading to improved efficiency.

23. Explain the concept of memoization in dynamic programming.

Ans:

Memoization is a technique used to optimize dynamic programming algorithms by storing the results of expensive function calls and returning the cached result when the same inputs occur again. It typically involves using a data structure, such as a dictionary or an array, to store the computed values along with their corresponding inputs. Memoization helps reduce redundant computations and improves the efficiency of dynamic programming algorithms, especially for problems with overlapping subproblems.

24. What is the difference between top-down and bottom-up dynamic programming?

Ans:

Top-down dynamic programming, also known as memoization, starts with the original problem and recursively solves smaller subproblems, storing the results in a memoization table to avoid redundant computations. Bottom-up dynamic programming, on the other hand, starts with the smallest subproblems and iteratively builds up the solution to the original problem by solving larger subproblems. While both approaches yield the same result, bottom-up dynamic programming tends to be more efficient and space-saving since it avoids the overhead of function call stack and recursion.

25. Explain the concept of backtracking and provide an example of its application.

Ans:

• Backtracking is a technique used to solve problems by recursively exploring all possible solutions and eliminating those that do not satisfy the problem constraints.
• It involves systematically searching the solution space and backtracking when a dead end is reached.
• An example of backtracking is the N-Queens problem, where the goal is to place N queens on an N×N chessboard such that no two queens threaten each other.

26. What is a branch-and-bound algorithm, and when is it used?

Ans:

Branch-and-bound is a technique for solving optimization problems. It involves systematically enumerating all possible solutions and pruning branches that do not lead to a better solution than the current best-known solution. This technique is typically used for combinatorial optimization problems, such as the travelling salesperson problem or the knapsack problem, where an exhaustive search is impractical due to the large solution space.

27. Explain the concept of a heuristic in algorithm design.

Ans:

A heuristic is a rule of thumb or a practical approach used to solve problems more efficiently, especially when an optimal solution is difficult or impossible to find in a reasonable amount of time. Heuristics often sacrifice optimality for efficiency by making informed guesses or approximations based on available information. Common examples of heuristics include greedy algorithms, genetic algorithms, and simulated annealing.

28. What is the role of randomness in algorithm design, and when are randomized algorithms used?

Ans:

Randomness plays a crucial role in algorithm design by introducing uncertainty or randomness into the algorithm’s behaviour. Randomized algorithms use random numbers to make decisions or computations, leading to probabilistic outcomes. They are often used in situations where the problem space is too large to explore exhaustively or when the input data is uncertain or noisy. Examples of randomized algorithms include quicksort with random pivot selection and the Monte Carlo method for numerical integration.

29. Explain the concept of approximation algorithms and when they are used.

Ans:

• Approximation algorithms are algorithms that find near-optimal solutions to optimization problems in polynomial time, even if an exact solution is computationally infeasible.
• They provide solutions that are guaranteed to be within a certain factor of the optimal solution, known as the approximation ratio.
• Approximation algorithms are used when finding an exact solution to a problem is NP-hard or impractical, but finding a good approximation quickly is sufficient for practical purposes.

30. What are some common techniques for reducing the time complexity of algorithms?

Ans:

Some common techniques for reducing the time complexity of algorithms include optimizing loop structures, minimizing unnecessary computations, using efficient data structures (such as hash tables, binary search trees, or heaps), applying algorithmic paradigms like divide and conquer or dynamic programming, parallelizing computations, and exploiting problem-specific properties or constraints. Additionally, algorithmic analysis and optimization tools, such as profiling and benchmarking, can help identify and eliminate bottlenecks in the algorithm.

31. Explain the concept of NP-hardness and NP-completeness. How are they related?

Ans:

NP-hardness refers to a problem’s difficulty, indicating that no known polynomial-time algorithm exists to solve it. NP-completeness, on the other hand, is a specific subset of NP-hard problems for which every problem in the NP class can be reduced to it in polynomial time. In other words, NP-completeness implies both NP-hardness and the property of being as hard as any problem in NP. Problems that are NP-complete are among the most challenging in computer science, as finding efficient solutions to them is unlikely.

32. Explain the concept of approximation ratio in approximation algorithms.

Ans:

• The approximation ratio of an approximation algorithm is a measure of how close the solution it provides is to the optimal solution for a given optimization problem.
• It’s defined as the ratio of the value of the approximate solution to the value of the optimal solution.
• A good approximation algorithm aims for a small approximation ratio, indicating that its solution is close to the optimal solution.
• The approximation ratio provides a quantitative measure of the quality of the approximation achieved by the algorithm.

33. What is the difference between deterministic and randomized algorithms? Provide examples of each.

Ans:

Deterministic algorithms always produce the same output for a given input and have predictable behaviour. Examples include sorting algorithms like merge sort and binary search. Randomized algorithms, on the other hand, use randomness or random numbers during their execution to achieve a desired result or improve efficiency. Examples include quicksort with random pivot selection and the Monte Carlo algorithm for estimating the value of pi.

34. Explain the concept of a reduction in the context of algorithm analysis.

Ans:

In algorithm analysis, reduction refers to the process of transforming one problem into another problem in a way that preserves the complexity of the original problem. It’s commonly used to show that one problem is at least as hard as another problem by demonstrating that if the second problem could be solved efficiently, then so could the first problem. Reductions are often used in proving NP-completeness and in designing approximation algorithms.

35. What are some common strategies for solving optimization problems using metaheuristic algorithms?

Ans:

• Some common strategies for solving optimization problems using metaheuristic algorithms include simulated annealing, genetic algorithms, ant colony optimization, particle swarm optimization, and tabu search.
• These algorithms typically use stochastic or probabilistic techniques to explore the solution space and escape local optima.
• They are well-suited for solving complex optimization problems where traditional methods may fail.

36. Explain the concept of a local search algorithm and provide an example of its application.

Ans:

A local search algorithm is a type of optimization algorithm that iteratively explores the neighbourhood of a current solution, making small incremental changes to improve it. It does not guarantee finding the global optimum but aims to find a satisfactory solution within a reasonable amount of time. An example of a local search algorithm is hill climbing, which repeatedly adjusts a single solution component to improve it until no further improvements are possible.

37. What is the travelling salesperson problem (TSP), and how is it typically solved?

Ans:

The travelling salesperson problem (TSP) is a classic optimization problem where the goal is to find the shortest possible route that visits each city exactly once and returns to the starting city. TSP is NP-hard, meaning that there is no known polynomial-time algorithm to solve it optimally for large instances. It’s typically solved using heuristic or approximation algorithms, such as a nearest neighbour, genetic algorithms, or simulated annealing, which provide near-optimal solutions in a reasonable amount of time.

38. Explain the concept of a greedy choice property in the context of greedy algorithms.

Ans:

• The greedy choice property states that at each step of a greedy algorithm, the locally optimal choice leads to a globally optimal solution.
• In other words, a greedy algorithm makes the best possible choice at each step without considering the consequences of that choice on future steps.
• This property is crucial for the correctness of greedy algorithms and is often proven using mathematical induction or contradiction.

39. What are some common techniques for solving integer programming problems?

Ans:

Some common techniques for solving integer programming problems include branch and bound, cutting-plane methods, branch and cut, and branch and price. These techniques efficiently explore the solution space and identify the optimal integer solution or prove optimality within a reasonable amount of time. Integer programming problems arise in various applications, such as resource allocation, scheduling, and network optimization.

40. Explain the concept of linear programming relaxation and its role in solving integer programming problems.

Ans:

Linear programming relaxation involves relaxing the integrality constraints of an integer programming problem, converting it into a linear programming problem that can be solved efficiently using standard techniques like the simplex method. The solution to the relaxed problem provides a lower bound on the optimal solution of the original integer programming problem. Linear programming relaxation is often used as a component of branch and bound algorithms for solving integer programming problems, helping guide the search for the optimal integer solution.

41. Explain the concept of parallel algorithms and their significance in algorithm design.

Ans:

• Parallel algorithms are designed to execute multiple tasks simultaneously, taking advantage of parallel processing architectures such as multi-core CPUs or distributed computing systems.
• They aim to improve the efficiency and performance of algorithms by dividing tasks into smaller, independent units that can be executed concurrently.
• Parallel algorithms are significant because they can exploit the computational power of modern hardware and solve large-scale problems more efficiently than sequential algorithms.

42. What are some common parallel algorithm design paradigms? Provide examples.

Ans:

Some common parallel algorithm design paradigms include task parallelism, where independent tasks are executed concurrently (e.g., parallel mergesort); data parallelism, where the same operation is performed on different data elements concurrently (e.g., parallel matrix multiplication); and pipeline parallelism, where tasks are divided into stages and executed in a pipeline fashion (e.g., parallel pipeline for image processing).

43. Explain the concept of MapReduce and its role in parallel and distributed computing.

Ans:

MapReduce is a programming model and framework for processing and generating large datasets in parallel and distributed computing environments. It divides a computation into two phases: the map phase, where input data is processed and transformed into key-value pairs, and the reduce phase, where the intermediate results are aggregated and combined to produce the final output. MapReduce is widely used for data-intensive tasks such as large-scale data processing, indexing, and web crawling.

44. What is the significance of algorithmic optimization techniques in practical algorithm design?

Ans:

• Algorithmic optimization techniques play a crucial role in practical algorithm design by improving their efficiency and performance.
• They aim to reduce algorithms’ time and space complexity, making them faster and more scalable for large-scale problems.
• Optimization techniques include algorithmic analysis, algorithmic profiling, code optimization, parallelization, and exploiting problem-specific properties or constraints.

45. Explain the concept of dynamic programming in the context of optimization problems.

Ans:

Dynamic programming is a technique for solving optimization problems by breaking them down into simpler subproblems and solving each subproblem only once. It involves storing the solutions to subproblems in a table and reusing them to solve larger subproblems, leading to improved efficiency. Dynamic programming is particularly useful for optimization problems with overlapping subproblems and optimal substructure properties, such as the knapsack problem or the longest common subsequence problem.

46. What are some common applications of dynamic programming algorithms in real-world problems?

Ans:

Dynamic programming algorithms are used in various real-world problems, including sequence alignment in bioinformatics, resource allocation and scheduling in operations research, route planning and shortest path algorithms in transportation and logistics, text processing and pattern matching in natural language processing, and image processing and computer vision tasks such as image segmentation and object recognition.

47. Explain the concept of a maximum subarray problem and provide an efficient algorithm to solve it.

Ans:

• The maximum subarray problem involves finding the contiguous subarray within an array of numbers that has the largest sum.
• An efficient algorithm to solve it is Kadane’s algorithm, which iterates through the array, maintaining two variables: the current maximum sum ending at the current position and the maximum sum seen so far.
• By updating these variables at each step, Kadane’s algorithm finds the maximum subarray sum in linear time complexity.

48. What is the difference between a linear programming problem and an integer programming problem?

Ans:

Linear programming problems involve optimizing a linear objective function subject to linear inequality and equality constraints, where the decision variables are continuous real numbers. Integer programming problems, on the other hand, are a generalization of linear programming problems where the decision variables are restricted to integer values. Integer programming problems are often more challenging to solve due to the combinatorial nature of the decision variables.

49. Explain the concept of a greedy choice property in the context of Huffman coding.

Ans:

In Huffman coding, the greedy choice property states that at each step of the algorithm, the two least frequent symbols are combined into a single composite symbol with a frequency equal to the sum of their frequencies. This process continues recursively until all symbols are combined into a binary tree, with the most frequent symbols closer to the root. The resulting binary tree represents the optimal prefix-free code for encoding the input symbols, with shorter codes assigned to more frequent symbols.

50. What are some common techniques for solving constraint satisfaction problems?

Ans:

Some common techniques for solving constraint satisfaction problems include backtracking, constraint propagation, local search algorithms such as simulated annealing or genetic algorithms, and constraint satisfaction programming (CSP) frameworks. These techniques aim to efficiently explore the solution space and find assignments to variables that satisfy all constraints, making them suitable for a wide range of combinatorial optimization problems.

51. Explain the concept of a greedy choice property in the context of Prim’s algorithm for minimum spanning trees.

Ans:

• In Prim’s algorithm for minimum spanning trees, the greedy choice property states that at each step, the algorithm selects the edge with the smallest weight that connects a vertex in the current tree to a vertex outside the tree.
• This locally optimal choice ensures that the algorithm always adds the edge that contributes the least to the total weight of the spanning tree.
• By repeatedly applying this property, Prim’s algorithm constructs a minimum spanning tree with optimal weight.

52. What is the Floyd-Warshall algorithm, and how does it work?

Ans:

The Floyd-Warshall algorithm is a dynamic programming algorithm used to find the shortest paths between all pairs of vertices in a weighted graph, including negative edge weights. It works by iteratively updating a matrix of shortest path distances between all pairs of vertices. Each iteration considers all possible intermediate vertices and updates the shortest path distances accordingly. After completing all iterations, the resulting matrix contains the shortest path distances between all pairs of vertices.

53. Explain the concept of NP-hardness in the context of decision problems.

Ans:

In the context of decision problems, NP-hardness refers to the property of a problem being at least as hard as the hardest problems in the NP class. A decision problem is NP-hard if every problem in NP can be reduced to it in polynomial time. This means that if an efficient algorithm exists for solving an NP-hard problem, then efficient algorithms also exist for solving all problems in NP, implying that P = NP. NP-hard problems are among the most challenging in computer science, as finding efficient solutions to them is unlikely.

54. What is the Knapsack problem, and how is it typically solved?

Ans:

• The Knapsack problem is a classic optimization problem where the goal is to maximize the value of items that can be included in a knapsack without exceeding its weight capacity.
• It’s typically solved using dynamic programming techniques, where the decision to include or exclude each item is made iteratively, considering the maximum value that can be achieved for each possible combination of items and knapsack capacities.

55. Explain the concept of a stable matching problem and provide an algorithm to solve it.

Ans:

In a stable matching problem, the goal is to find a matching between two sets of elements such that there are no unstable pairs, where an unstable pair consists of two elements who prefer each other over their current partners. The Gale-Shapley algorithm is a popular algorithm to solve the stable matching problem. It involves iteratively proposing and accepting or rejecting matches between elements from one set to the other until a stable matching is found.

56. What is the travelling salesperson problem (TSP), and how is it typically solved?

Ans:

• The travelling salesperson problem (TSP) is a classic optimization problem where the goal is to find the shortest possible route that visits each city exactly once and returns to the starting city.
• TSP is NP-hard, meaning that there is no known polynomial-time algorithm to solve it optimally for large instances.
• It’s typically solved using heuristic or approximation algorithms, such as a nearest neighbour, genetic algorithms, or simulated annealing, which provide near-optimal solutions in a reasonable amount of time.

57. Explain the concept of a matching problem and provide an algorithm to solve it.

Ans:

In a matching problem, the goal is to find a subset of edges in a graph such that no two edges share a common vertex. The maximum matching problem seeks to find the largest possible matching, while the maximum weight matching problem aims to maximize the sum of weights of the edges in the matching. The Ford-Fulkerson algorithm, also known as the augmenting path algorithm, is commonly used to solve maximum matching problems by iteratively augmenting the matching until no further improvements are possible.

58. What is the concept of amortized analysis, and how is it used to analyze the time complexity of algorithms?

Ans:

Amortized analysis is a method for analyzing the average time or space complexity of a sequence of operations on a data structure. It considers the total cost of a series of operations divided by the number of operations, providing an average cost per operation. Amortized analysis is particularly useful for analyzing data structures with expensive individual operations but overall efficient performance, such as dynamic arrays or hash tables.

59. Explain the concept of a flow network and provide an example of its application.

Ans:

• A flow network is a directed graph where each edge has a capacity and represents the maximum amount of flow that can be sent from one vertex to another.
• It’s commonly used to model transportation or network flow problems, such as the maximum flow problem, where the goal is to find the maximum amount of flow that can be sent from a source vertex to a sink vertex without violating capacity constraints along the paths.

60. What is the concept of network flow algorithms, and how are they used in practical applications?

Ans:

Network flow algorithms solve optimization problems involving flow networks, such as the maximum flow problem, minimum cut problem, or circulation problem. They are applied in various practical applications, including transportation and logistics, telecommunications, computer networking, and supply chain management, to optimize resource allocation, minimize costs, or maximize efficiency in flow networks.

61. Explain the concept of the Bellman-Ford algorithm and its application.

Ans:

The Bellman-Ford algorithm is used to find the shortest paths from a single source vertex to all other vertices in a weighted graph, even in the presence of negative edge weights. It iteratively relaxes the edges in the graph by considering all possible paths from the source vertex to each destination vertex and updating the shortest path distances accordingly. The algorithm detects negative weight cycles and reports if they exist. Bellman-Ford is commonly used in network routing protocols and distributed systems.

62. What is the concept of maximum bipartite matching, and how is it typically solved?

Ans:

• Maximum bipartite matching is a problem where the goal is to find the largest possible matching between two disjoint sets of vertices in a bipartite graph, such that each vertex is matched with at most one vertex from the other set.
• It can be solved using algorithms such as the Hopcroft-Karp algorithm or Ford-Fulkerson algorithm with appropriate modifications for bipartite graphs.
• Applications include resource allocation, assignment problems, and stable marriage problems.

63. Explain the concept of branch and bound and its application in algorithm design.

Ans:

Branch and bound is a systematic algorithmic technique used to solve optimization problems by exploring the solution space in a tree-like fashion, pruning branches that cannot lead to better solutions than the current best-known solution. It’s commonly used in problems such as integer programming, travelling salesman problems, and knapsack problems, where the search space is too large to explore exhaustively. Branch and bound improves efficiency by intelligently pruning branches based on lower bounds and feasible solutions.

64. What is the concept of integer linear programming, and how is it typically solved?

Ans:

Integer linear programming (ILP) is a mathematical optimization technique in which the decision variables are restricted to integer values. The goal is to find the optimal values of these variables to minimize or maximize an objective function subject to linear inequality and equality constraints. ILP problems can be solved using optimization solvers such as the simplex method, interior point methods, or branch and bound algorithms. Applications include production planning, scheduling, and resource allocation problems.

65. Explain the concept of dynamic programming in the context of grid-based problems.

Ans:

• Dynamic programming is commonly used to solve grid-based problems, where the goal is to find optimal paths, sequences, or values in a grid-like structure.
• It involves breaking down the problem into smaller subproblems, storing the solutions to these subproblems in a table, and reusing them to solve larger subproblems.
• Dynamic programming is particularly useful for problems such as shortest path algorithms (e.g., Dijkstra’s algorithm), sequence alignment (e.g., Smith-Waterman algorithm), and optimal substructure problems (e.g., longest increasing subsequence).

66. What is the concept of a stable marriage problem, and how is it typically solved?

Ans:

The stable marriage problem is a combinatorial optimization problem in which the goal is to find a stable match between two sets of elements, such as men and women, based on their preferences. A match is considered stable if there are no pairs of elements that would prefer each other over their current partners. The Gale-Shapley algorithm, also known as the deferred acceptance algorithm, is commonly used to solve the stable marriage problem by iteratively proposing and accepting or rejecting matches until a stable matching is found.

67. Explain the concept of a multistage graph and provide an example of its application.

Ans:

A multistage graph is a directed graph with multiple layers of vertices, where each layer represents a stage or phase of a process, and edges connect vertices between adjacent layers. It’s commonly used to model optimization problems such as project scheduling, job sequencing, and manufacturing processes, where tasks or activities must be performed in sequential stages with precedence constraints. Dynamic programming algorithms are often applied to find optimal solutions to multistage graph problems efficiently.

68. What is the concept of network flow algorithms, and how are they used in practical applications?

Ans:

• Network flow algorithms solve optimization problems involving flow networks, such as the maximum flow problem, minimum cut problem, or circulation problem.
• They are applied in various practical applications, including transportation and logistics, telecommunications, computer networking, and supply chain management, to optimize resource allocation, minimize costs, or maximize efficiency in flow networks.

69. Explain the concept of a matching problem and provide an algorithm to solve it.

Ans:

In a matching problem, the goal is to find a subset of edges in a graph such that no two edges share a common vertex. The maximum matching problem seeks to find the largest possible matching, while the maximum weight matching problem aims to maximize the sum of weights of the edges in the matching. The Ford-Fulkerson algorithm, also known as the augmenting path algorithm, is commonly used to solve maximum matching problems by iteratively augmenting the matching until no further improvements are possible.

70. What is the concept of the stable roommate’s problem, and how is it typically solved?

Ans:

The stable roommate problem is a variation of the stable marriage problem where each participant ranks all other participants in order of preference, and the goal is to find a stable match where no pair of participants prefers each other over their current partners. The algorithm to solve the stable roommate’s problem is similar to the Gale-Shapley algorithm used for stable marriage but with modifications to handle the absence of gender constraints. It involves iteratively proposing and accepting or rejecting matches until a stable match is found.

71. Explain the concept of divide and conquer in algorithm design and provide an example of its application.

Ans:

• Divide and conquer is a problem-solving paradigm in which a problem is divided into smaller subproblems, solved recursively, and then combined to find the solution to the original problem.
• An example of its application is the merge sort algorithm, which divides an array into two halves, recursively sorts each half, and then merges the sorted halves to produce a sorted array.
• Merge sort exhibits the divide and conquer strategy by breaking down the sorting problem into smaller subproblems and then combining the sorted solutions.

72. What is the concept of the maximum subarray problem, and how is it typically solved?

Ans:

The maximum subarray problem involves finding the contiguous subarray within an array of numbers that has the largest sum. It’s typically solved using Kadane’s algorithm, which iterates through the array, maintaining two variables: the current maximum sum ending at the current position and the maximum sum seen so far. By updating these variables at each step, Kadane’s algorithm finds the maximum subarray sum in linear time complexity.

73. Explain the concept of backtracking and provide an example of its application in algorithm design.

Ans:

Backtracking is a technique for solving problems by recursively exploring all possible solutions and eliminating those that do not satisfy the problem constraints. An example of its application is the N-Queens problem, where the goal is to place N queens on an N×N chessboard such that no two queens threaten each other. Backtracking is used to explore all possible queen placements, ensuring that no two queens share the same row, column, or diagonal.

74. What is the concept of memoization, and how is it used to optimize recursive algorithms?

Ans:

• Memoization is a technique used to optimize recursive algorithms by storing the results of expensive function calls and returning the cached result when the same inputs occur again.
• It typically involves using a data structure, such as a dictionary or an array, to store the computed values along with their corresponding inputs.
• Memoization helps reduce redundant computations and improves the efficiency of recursive algorithms, especially for problems with overlapping subproblems.

75. Explain the concept of backtracking and provide an example of its application in algorithm design.

Ans:

Backtracking is a technique for solving problems by recursively exploring all possible solutions and eliminating those that do not satisfy the problem constraints. An example of its application is the N-Queens problem, where the goal is to place N queens on an N×N chessboard such that no two queens threaten each other. Backtracking is used to explore all possible queen placements, ensuring that no two queens share the same row, column, or diagonal.

76. What is the concept of memoization, and how is it used to optimize recursive algorithms?

Ans:

Memoization is a technique used to optimize recursive algorithms by storing the results of expensive function calls and returning the cached result when the same inputs occur again. It typically involves using a data structure, such as a dictionary or an array, to store the computed values along with their corresponding inputs. Memoization helps reduce redundant computations and improves the efficiency of recursive algorithms, especially for problems with overlapping subproblems.

77. Explain the concept of backtracking and provide an example of its application in algorithm design.

Ans:

• Backtracking is a technique for solving problems by recursively exploring all possible solutions and eliminating those that do not satisfy the problem constraints.
• An example of its application is the N-Queens problem, where the goal is to place N queens on an N×N chessboard such that no two queens threaten each other.
• Backtracking is used to explore all possible queen placements, ensuring that no two queens share the same row, column, or diagonal.

78. What is the concept of memoization, and how is it used to optimize recursive algorithms?

Ans:

Memoization is a technique used to optimize recursive algorithms by storing the results of expensive function calls and returning the cached result when the same inputs occur again. It typically involves using a data structure, such as a dictionary or an array, to store the computed values along with their corresponding inputs. Memoization helps reduce redundant computations and improves the efficiency of recursive algorithms, especially for problems with overlapping subproblems.

79. Explain the travelling salesperson problem (TSP) and provide an example of its application.

Ans:

The travelling salesperson problem (TSP) is a classic optimization problem where the goal is to find the shortest possible route that visits each city exactly once and returns to the starting city. An example of its application is in logistics, where a salesperson needs to visit multiple cities to deliver goods or services while minimizing travel distance or time.

80. What is the concept of the knapsack problem, and how is it typically solved?

Ans:

• The knapsack problem is a combinatorial optimization problem where the goal is to maximize the value of items that can be included in a knapsack without exceeding its weight capacity.
• It’s typically solved using dynamic programming techniques, where the decision to include or exclude each item is made iteratively, considering the maximum value that can be achieved for each possible combination of items and knapsack capacities.

81. Explain the concept of Big O notation in algorithm analysis and its significance.

Ans:

Big O notation is a mathematical notation used to describe the upper bound or worst-case time complexity of an algorithm in terms of the input size. It provides a way to classify algorithms based on their scalability and efficiency as the input size grows. For example, an algorithm with a time complexity of O(n^2) means that its running time grows quadratically with the size of the input. Big O notation is significant because it helps algorithm designers and developers understand and compare the efficiency of different algorithms and make informed decisions about algorithm selection and optimization.

82. What are some common sorting algorithms, and how do they differ in terms of time complexity and performance?

Ans:

Some common sorting algorithms include bubble sort, selection sort, insertion sort, merge sort, quicksort, and heapsort. These algorithms differ in terms of their time complexity, performance characteristics, and suitability for different types of data. For example, bubble sort and selection sort have a time complexity of O(n^2) and are suitable for small datasets. At the same time, merge sort and quicksort have a time complexity of O(n log n) and are more efficient for large datasets. Heapsort has a time complexity of O(n log n) but is more memory-efficient than merge sort and quicksort.

83. Explain the concept of stable and unstable sorting algorithms. Provide examples of each.

Ans:

• A stable sorting algorithm preserves the relative order of equal elements in the input array.
• In other words, if two elements have the same value and appear in a specific order in the input, they will also appear in the same order in the output.
• Examples of stable sorting algorithms include merge sort, insertion sort, and bubble sort.
• Conversely, an unstable sorting algorithm does not guarantee the preservation of the relative order of equal elements.
• Examples of unstable sorting algorithms include quicksort and heapsort.

84. What is the concept of binary search, and how does it work?

Ans:

Binary search is a divide-and-conquer algorithm used to search for a target value in a sorted array or list. It works by repeatedly dividing the search interval in half and comparing the target value with the middle element. If the target value matches the middle element, the search is successful. If the target value is less than the middle element, the search continues in the lower half of the array. If the target value is greater than the middle element, the search continues in the upper half of the array. Binary search has a time complexity of O(log n) and is significantly more efficient than linear search for large datasets.

85. Explain the concept of a hash table and its role in algorithm design.

Ans:

A hash table is a data structure that stores key-value pairs and allows for efficient insertion, deletion, and lookup operations. It works by mapping keys to array indices using a hash function, which computes a unique index for each key. Hash tables are commonly used in algorithm design for tasks such as implementing associative arrays, symbol tables, and frequency counting. They provide constant-time average-case performance for insertion, deletion, and lookup operations, making them suitable for a wide range of applications.

86. What are some common graph traversal algorithms, and how do they differ in terms of their approach and applications?

Ans:

• Some common graph traversal algorithms include depth-first search (DFS) and breadth-first search (BFS). DFS explores as far as possible along each branch before backtracking, making it suitable for tasks such as cycle detection, topological sorting, and connected component identification.
• BFS explores all neighbour nodes at the current depth level before moving to the next depth level, making it suitable for tasks such as shortest path finding, minimum spanning tree construction, and network flow analysis.
• The choice of traversal algorithm depends on the specific requirements of the problem and the properties of the graph.

87. Explain the concept of dynamic programming in algorithm design and provide an example of its application.

Ans:

Dynamic programming is a technique used to solve optimization problems by breaking them down into simpler subproblems and solving each subproblem only once. It involves storing the solutions to subproblems in a table and reusing them to solve larger subproblems, leading to improved efficiency. An example of its application is the knapsack problem, where the goal is to maximize the value of items that can be included in a knapsack without exceeding its weight capacity. Dynamic programming algorithms, such as the 0/1 knapsack algorithm, efficiently find the optimal solution by considering all possible combinations of items and knapsack capacities.

88. Explain the concept of a greedy algorithm and provide an example of its application.

Ans:

A greedy algorithm is an algorithmic paradigm that makes locally optimal choices at each step with the hope of finding a global optimum. It does not necessarily guarantee an optimal solution, but it often provides a good approximation in a reasonable amount of time. An example of its application is the greedy algorithm for the coin change problem, where the goal is to make change for a given amount using the fewest possible coins of given denominations. The greedy algorithm selects the largest denomination coin that is less than or equal to the remaining amount at each step, leading to an optimal solution in this case.

89. Explain the concept of backtracking in algorithm design and provide an example of its application.

Ans:

• Backtracking is a technique used to solve problems by recursively exploring all possible solutions and eliminating those that do not satisfy the problem constraints.
•  It involves systematically searching the solution space and backtracking when a dead end is reached.
• An example of its application is the N-Queens problem, where the goal is to place N queens on an N×N chessboard such that no two queens threaten each other.
• Backtracking is used to explore all possible queen placements and backtrack when a conflict is detected, ultimately finding all possible solutions to the problem.

90. Explain the concept of branch and bound in algorithm design and provide an example of its application.

Ans:

Branch and bound is a systematic algorithmic technique used to solve optimization problems by exploring the solution space in a tree-like fashion. These pruning branches cannot lead to better solutions than the current best-known solution. It’s commonly used in problems such as integer programming, travelling salesman problems, and knapsack problems, where the search space is too large to explore exhaustively. An example of its application is the branch and bound algorithm for the travelling salesperson problem, which systematically explores

91. Explain the concept of the Floyd-Warshall algorithm and its application.

Ans:

The Floyd-Warshall algorithm finds the shortest paths between all pairs of vertices in a weighted graph, even in the presence of negative edge weights. It works by iteratively updating a matrix of shortest path distances between all pairs of vertices. Each iteration considers all possible intermediate vertices and updates the shortest path distances accordingly. The algorithm detects negative weight cycles and reports if they exist. The Floyd-Warshall algorithm is commonly used in network routing protocols, traffic management systems, and geographical information systems.

92. What is the concept of NP-completeness in algorithm analysis, and why is it important?

Ans:

• NP-completeness is a property of decision problems that belong to the class NP and are at least as hard as the hardest problems in NP.
• A problem is NP-complete if every problem in NP can be reduced to it in polynomial time.
• NP-completeness is important because it provides a way to classify and compare the computational complexity of optimization problems.
• If an efficient algorithm exists for solving an NP-complete problem, then efficient algorithms also exist for solving all problems in NP, implying that P = NP.
• NP-complete problems are among the most challenging in computer science, and proving NP-completeness can help establish the intractability of a problem.

93. Explain the concept of memoization in dynamic programming and its significance.

Ans:

Memoization is a technique used to optimize recursive algorithms by storing the results of expensive function calls and returning the cached result when the same inputs occur again. It typically involves using a data structure, such as a dictionary or an array, to store the computed values along with their corresponding inputs. Memoization helps reduce redundant computations and improves the efficiency of recursive algorithms, especially for problems with overlapping subproblems. It is a key technique in dynamic programming, allowing for efficient solution of optimization problems by avoiding repeated computations.

94. What is the concept of the stable marriage problem, and how is it typically solved?

Ans:

The stable marriage problem is a combinatorial optimization problem in which the goal is to find a stable match between two sets of elements, such as men and women, based on their preferences. A match is considered stable if there are no pairs of elements that would prefer each other over their current partners. The Gale-Shapley algorithm, also known as the deferred acceptance algorithm, is commonly used to solve the stable marriage problem by iteratively proposing and accepting or rejecting matches until a stable matching is found.

95. Explain the concept of the longest common subsequence problem and its significance.

Ans:

• The longest common subsequence (LCS) problem is a classic dynamic programming problem in which the goal is to find the longest subsequence common to two sequences.
• A subsequence is a sequence that appears in the same relative order but is not necessarily contiguous.
• The LCS problem is significant because it has applications in bioinformatics, text comparison, version control systems, and plagiarism detection.
• It can be efficiently solved using dynamic programming techniques by building a table of longest common subsequences for subproblems of increasing sizes.

96. What is the concept of the travelling salesperson problem (TSP), and why is it important?

Ans:

The travelling salesperson problem (TSP) is a classic optimization problem where the goal is to find the shortest possible route that visits each city exactly once and returns to the starting city. TSP is important because it has applications in logistics, transportation, scheduling, and network optimization. Finding an optimal solution to the TSP is NP-hard, meaning that there is no known polynomial-time algorithm to solve it optimally for large instances. However, approximate solutions can be found using heuristic algorithms such as a nearest neighbour, genetic algorithms, or simulated annealing.

97. Explain the concept of Dijkstra’s algorithm and its application.

Ans:

Dijkstra’s algorithm is used to find the shortest paths from a single source vertex to all other vertices in a weighted graph with non-negative edge weights. It works by iteratively selecting the vertex with the smallest distance from the source vertex and relaxing its adjacent vertices, updating their distances if a shorter path is found. Dijkstra’s algorithm is commonly used in network routing protocols, pathfinding algorithms in computer games and robotics, and geographical information systems

98. What is the concept of the maximum flow problem, and how is it typically solved?

Ans:

• The maximum flow problem is a classic optimization problem where the goal is to find the maximum amount of flow that can be sent from a source vertex to a sink vertex in a flow network.
• It’s typically solved using network flow algorithms such as the Ford-Fulkerson algorithm or the Edmonds-Karp algorithm.
• These algorithms use techniques such as augmenting paths and residual capacities to iteratively increase the flow until no further improvements are possible.

99. Explain the concept of NP-hardness in algorithm analysis and provide an example of an NP-hard problem.

Ans:

NP-hardness refers to the property of a problem being at least as hard as the hardest problems in the NP class. A problem is NP-hard if every problem in NP can be reduced to it in polynomial time. This means that if an efficient algorithm exists for solving an NP-hard problem, then efficient algorithms also exist for solving all problems in NP, implying that P = NP. An example of an NP-hard problem is the subset sum problem, where the goal is to determine whether there exists a subset of a given set of integers that sums to a target value.