45+ Linked list Interview Questions and Answers

A linked list is a linear data structure in which items are kept in individual objects known as nodes. Each node includes one or more data elements as well as a reference to the next node in the sequence. Unlike arrays, linked lists do not require contiguous memory allocation, allowing for more efficient insertion and deletion operations. Accessing entries in a linked list, on the other hand, might be slower than accessing elements in an array since it involves traversing the list from the start.

1. What’s a linked list?

Ans:

A linked list is a foundational data structure in computer wisdom, designed to store collections of particulars not in conterminous memory locales. Each element, known as a node, holds two pieces of information: the data of the element and a reference( or pointer) to the coming node in the sequence. This structure enables efficient insertion and deletion of elements by adjusting pointers, unlike arrays that require shifting elements.

2. How do independently linked lists differ from twice-linked lists?

Ans:

Independently and doubly linked lists differ in node connections. An independently linked list has nodes with a single reference to the next node, allowing efficient forward traversal. A doubly linked list has nodes with two references—one to the next and one to the previous node—enabling both forward and backward traversal. This adds flexibility but requires more memory and complicates insertion and deletion.

3. What are the advantages of linked lists over arrays?

Ans:

• Linked lists offer several advantages over arrays, particularly in terms of dynamic memory allocation and ease of insertion and omission operations.
• Since linked lists don’t bear a conterminous block of memory, they can grow stoutly with the program’s requirements without the need for resizing.
• Insertions and elisions are more effective because they only involve reassigning pointers, not shifting multiple elements as in arrays.
• This inflexibility comes at the cost of slower access times, as linked lists need to support direct access to their elements by indicator.

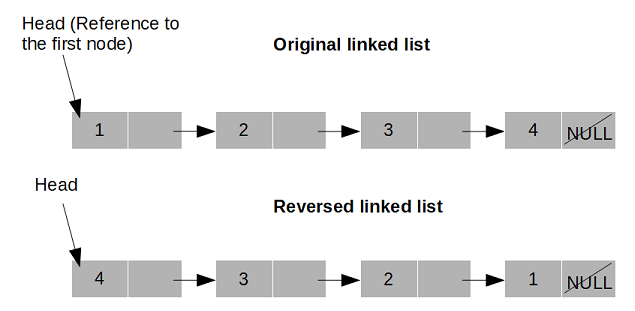
4. What are the steps to reverse a linked list?

Ans:

Reversing a linked list involves changing the direction of the pointers between bumps so that the first node becomes the last and vice versa. This can be achieved through an iterative process where you cut the List, conforming pointers as you go. Specifically, you maintain three pointers: the former node( prev), the current node( current), and the coming node( coming). At each step, you save the coming node, reverse the current node’s pointer to point to the former node, and also move the previous and current pointers one step forward.

5. What’s an indirect linked list, and how does it differ from a regular linked list?

Ans:

An indirectly linked list is a variation of the linked List in which the last node’s coming pointer isn’t set to NULL( as in a typical linked list) but rather points back to the first node. This creates an indirect structure that allows for endless traversal of the List. Indirectly linked lists can be either independently or twice linked. The primary advantage of indirect lists is that they allow for a natural perpetration of cyclically repeating tasks, similar to round-robin scheduling.

6. What defines a cycle in a linked list?

Ans:

• Detecting a cycle in a linked list is a common problem that can be efficiently answered using Floyd’s Tortoise and Hare algorithm.
• This fashion involves using two-pointers that move at different pets. One advances through the List one node at a time( the tortoise), and the other moves two bumps at a time( the hare). 
• Still, the hare and tortoise will ultimately meet within the cycle If the linked List contains a cycle. However, the List doesn’t contain a cycle If the hare reaches the end of the List ( NULL).
• This system provides a way to describe cycles without demanding redundant storehouses for visited bumps, making it effective in terms of both time and space.

7. What method allows finding the middle element of a linked list in a single pass?

Ans:

Chancing the middle element of a linked list in a single pass can be efficiently achieved using the Tortoise and Hare algorithm, analogous to detecting a cycle. In this approach, two pointers are used: one( the hare) advances two bumps at a time, while the other( the tortoise) advances one node at a time. By the time the hare reaches the end of the List, the tortoise will be at the midpoint. This method works well for both even and odd numbers of elements, providing a simple way to find the middle element without knowing the list length in advance.

8. How do users combine two sorted linked lists into a single sorted linked list?

Ans:

Incorporating two sorted linked lists involves creating a new list that preserves the order of elements from both input lists. Start with an ersatz head node to simplify edge cases and maintain a current pointer to construct the new List. At each step, compare the values of the current bumps in both lists, subjoining the lower value to the new List and moving the pointer forward in the List from which the element was taken. Continue this process until all elements from both lists have been intermingled.

9. What are the complications involved in various linked list operations?

Ans:

In a linked list, time complexity varies by operation: accessing or searching for an element is (O(n)) due to potential full traversal. Inserting or deleting at the head is (O(1)), but at a specific position or end can be (O(n)) due to traversal. The space complexity is (O(n)), with (n) being the number of elements, as each node needs space for its data and pointers. Understanding these complexities is key for evaluating linked list efficiency.

10. Explain the difference between independently linked lists and twice linked lists.

Ans:

Feature	Singly Linked List	Doubly Linked List
Node Structure	Data + Next Pointer	Data + Next + Previous Pointers
Traversal	Forward Only	Forward and Backward
Memory Usage	Lower	Higher
Insertion/Deletion	Simpler	Slightly More Complex

11. What’s a memory leak in the environment of linked lists, and how can it be averted?

Ans:

• A memory leak in linked lists occurs when bumps are removed, or the entire List is deleted without duly relocating the memory used by the bumps. This leads to wasted memory coffers that the program can no longer use.
• In languages like C or C, where homemade memory operations are needed, it’s pivotal to explicitly free the memory allocated for each node after it is no longer demanded.
• This involves repeating over the List and using the free or delete keyword on each node after ensuring no references are left pointing to it. Careful operation of pointers and memory is essential to help prevent leaks and ensure resource effectiveness.

12. Explain the conception of an” ersatz head” node in a linked list.

Ans:

An “ersatz head” node, also known as a guard node, is a fashion used to simplify the running of edge cases in linked list operations, especially insertions and elisions on the morning of the List or in an empty list. The ersatz head is a placeholder node that doesn’t contain factual data applicable to the List’s contents but serves as the original head of the List. By maintaining at least one node (the ersatz head), algorithms avoid explicit null checks for the head node.

13. What is an efficient way to remove duplicates from an unsorted linked list?

Ans:

Removing duplicates from an unsorted linked list requires relating and deleting any bumps that have data values that appear further than previously. A common approach involves using a hash table to track seen values as you cut the List. Start by initializing an empty hash table and a pointer to reiterate through the linked List, with a former pointer to manage elisions. Check if the value of each node exists in the hashtable.

14. What’s the significance of the” runner” fashion in linked list problems?

Ans:

The “runner” or “two-pointer” technique is highly effective for linked list problems. It uses two pointers that move at different speeds or start at different times. This method is useful for detecting cycles, finding the middle element, and locating the nth-to-last element. It allows operations to be performed in a single pass through the list, optimizing time complexity where direct access to elements is not possible, unlike arrays.

15. What is the process to find the intersection point of two linked lists?

Ans:

• Chancing the crossroad point of two linked lists, where they combine into a single sequence, involves many strategic ways to handle lists of different lengths. First, calculate the lengths of both lists.
• Next, advance the pointer in the longer List by the difference in lengths, ensuring both pointers are equidistant from the implicit crossroad point.
• Also, contemporaneously advance both pointers through their separate lists, comparing bumps for equivalency( by reference, not by value).
• When the pointers meet on the same node, that node is the crossroad point. However, the lists don’t cross If they reach the end without clustering.

16. How can a linked list be used to apply a hash table?

Ans:

A linked list can be an essential element in enforcing a hash table, particularly to handle collisions through a system known as chaining. In this approach, the hash table is an array of linked list heads, each representing a pail. When an element is fitted, its hash value determines the corresponding bucket. However, they’re stored in a linked list at that array indicator If multiple elements hash to the same pail. This allows for effective insertions, elisions, and lookups, as the linked List can stoutly grow to accommodate entries and handle collisions gracefully.

17. What challenges arise when implementing a linked list in a low-level language like C?

Ans:

• Enforcing a linked list in a low-position language like C introduces several challenges and considerations, primarily around memory operation, pointer manipulation, and error running.
• Careful allocation and deallocation of memory using malloc and free are pivotal to help memory leaks and ensure effective use of coffers.
• Pointer manipulation must be done cautiously to avoid segmentation faults or corrupting the list structure, particularly when fitting or deleting bumps.
• Also, programmers must vigilantly check for and handle crimes similar to null pointer dereferences or memory allocation failures.

18. Explain how a twice-linked list can be used to apply a deque structure.

Ans:

A twice-linked list is immaculately suited for enforcing a deque(double-concluded line), as it allows for effective insertion and omission operations at both ends. In a deque, elements can be added or removed from both the front( head) and back( tail) of the line. A twice-linked list supports these operations innately due to its two-way liaison. Each node points to both its precursor and successor. Adding or removing elements from either end of the List can be done in constant time, O( 1), by conforming many pointers without demanding to cut the List.

19. How is a linked list implemented in languages with automatic garbage collection, like Java or Python?

Ans:

• Enforcing a linked list in a language with automatic scrap collection, similar to Java or Python, simplifies memory operation enterprises.
• The focus shifts towards designing the node class( or original structure) to hold data and link( s) to other bumps.
• For an independently linked list, each node generally contains a data field and a reference to the coming node.
• In these languages, when any part of your program no longer substantiates a node, the scrap collector automatically reclaims the memory, barring homemade memory deallocation and reducing the threat of memory leaks. 

20. What’s the’ slow-fast pointer’ fashion, and how is it used in linked list problems?

Ans:

• The’ slow-fast pointer’ fashion, also known as the Tortoise and Hare algorithm, involves two pointers that move through the linked List at different pets.
• This fashion is particularly useful for relating cycles, chancing the middle element, and working Floyd’s cycle discovery problem in linked lists.
• The difference in pets allows the fast pointer to reevaluate and meet the slow pointer if there’s a cycle, indicating the cycle’s presence.
• Also, when the fast pointer reaches the end of the List, the slow pointer will be at the midpoint, allowing for effective middle element identification without demanding to know the List’s length.

21. How can you split a linked list into two equal parts?

Ans:

To split a singly linked list into two equal halves, use the slow-fast pointer technique. Move the slow pointer one step at a time and the fast pointer two steps at a time. When the fast pointer reaches the end, the slow pointer will be at the middle. Cut the list at this middle node to create two separate lists. Adjust the pointers: the last node of the first list should point to ‘null’, and the end of the second list should point to ‘null’ as well, effectively splitting the list into two.

22. What are guard bumps, and how are they used in linked list executions?

Ans:

Sentinel bumps, or ersatz bumps, are special bumps in a linked list that don’t hold any factual data applicable to the List’s intended use but serve as placeholders to simplify operations like insertions, elisions, and boundary conditions. By incorporating a guard node, generally in the morning( and occasionally at the end) of the List, you can avoid handling special cases for operations at the List’s boundaries. For illustration, fitting or deleting at the morning or end of the List doesn’t bear tentative checks to determine if the List is empty.

23. Explain how to find the utmost node from the end of a linked list.

Ans:

Chancing the utmost node from the end of a linked list in a single pass can be efficiently fulfilled using the two-pointer fashion. Start with two pointers, both on the morning of the List. Move the one-pointer ( the lead pointer) and bump it ahead in the List. Also, move both pointers forward contemporaneously until the lead pointer reaches the end of the List. At this point, the running pointer will be at the utmost node from the end. This method uses the gap between two pointers to measure the distance from the List’s end, eliminating the need to first determine the List’s length.

24. How can users sort a linked list?

Ans:

• Sorting a linked list can be approached with various algorithms, with Merge Sort being particularly effective due to its effectiveness and felicity for linked lists. 
• Combine kind divides the List into two halves, recursively feathers each half, and also merges the two sorted halves back together.
• The division into halves can be achieved using the slow-fast pointer fashion to find the middle of the List. The merge process involves re-linking bumps in sorted order, which is effective in a linked list environment.
• Unlike array-ground sorting algorithms, which frequently calculate on arbitrary access, combination kind’s successional access pattern matches well with the linked list structure, leading to effective sorting indeed for large lists.

25. What is the method to detect and remove a loop in a linked list?

Ans:

Detecting and removing a circle in a linked list can be done using Floyd’s CycleChancing algorithm, also known as the tortoise and hare algorithm. First, use two pointers moving at different pets to describe a circle, as they will ultimately meet inside the circle if one exists. Once a circle is detected, to find the circle’s starting node, move one pointer to the head of the List while keeping the other at the meeting point, and also move both at the same speed.

26. What are the advantages and disadvantages of using a linked list over an array?

Ans:

• Linked lists offer several advantages over arrays, including dynamic size, ease of insertion and omission operations, and effective memory application as they allocate memory as demanded.
• Unlike arrays, linked lists don’t bear a conterminous block of memory, allowing for flexible data structure growth and loss without the need for resizing or reallocating memory, which can be expensive operations in arrays.
• Still, linked lists have disadvantages, similar to poor cache performance due to a to-contiguous memory storehouse, leading to advanced access times.
• Also, they warrant direct access to elements, meaning operations that bear penetrating elements at arbitrary positions are generally slower, taking O(n) time to cut the List up to that point.

27. How do you implement a heap and a queue using linked lists?

Ans:

Enforcing a mound or line with a linked list involves exercising the List’s dynamic nature to efficiently perform insertions and elisions. For a mound, which follows a last-in-first-eschewal (LIFO) principle, you can add and remove elements from the head of the List to achieve O(1) drive and pop operations. For a line which operates on a first-in-first-eschewal (FIFO) base, elements are enqueued( added) at the tail and dequeued( removed) from the head.

28. How can users efficiently concatenate two independently linked lists?

Ans:

• Concatenating two independently linked lists efficiently requires linking the end of the first List to the morning of the alternate.
• This operation is straightforward if you maintain a tail pointer for the first List, as it involves simply setting the coming pointer of the tail node of the first List to the head of the alternative.
• However, you must cut the first List to find its last node, which can take O(n) time, where n is the length of the first List if a tail pointer isn’t maintained.
• After setting the last node’s coming pointer of the first List to point to the head of the alternate List, the lists are effectively concatenated.

29. Discuss the impact of linked lists in recursive algorithms.

Ans:

Linked lists play a significant part in recursive algorithms due to their essential recursive structure; each node can be seen as the head of a lower list. This characteristic makes linked lists ideal for recursive operations, similar to reversing, searching, or sorting through peak-and-conquer ways. Recursive algorithms can navigate and manipulate linked lists with minimum state operation, as the recursion mound implicitly tracks the algorithm’s progress through the List.

30. What is the process for serializing and deserializing a linked list?

Ans:

• Reissuing a linked list involves converting its bumps and their connections into a flat format that can be stored or transmitted and also reconstructed(deserialized) into the original linked list structure.
• To contribute, you can cut the List and store each node’s data( and conceivably its pointers if the list structure is non-linear or includes references to non-sequential bumps) in an array or string format.
• Deserialization involves reading the serial data and reconstructing the bumps and pointers according to the stored sequence and connections.
• For complex linked list structures, similar to those with arbitrary pointers, a mapping from original node references to their reissued counterparts may be necessary during serialization to rightly restore the pointers during deserialization.

31. What’s the time complexity of fitting a node in a sorted linked list?

Ans:

• Fitting a node in a sorted linked list requires covering the List from the morning to find the correct insertion point where the new node’s value is in the correct order. This traversal process takes O( n) time in the worst case, where
•  n is the number of bumps in the List, as the insertion point could potentially be at the end of the List. Once the insertion point is linked, fitting the node itself is an O( 1) operation, as it requires only conforming the coming pointers of the conterminous bumps.
• Thus, the overall time complexity of fitting a node into a sorted linked list is O( n), dominated by the traversal time to find the applicable insertion point.

32. How can you implement a doubly linked list without using a ‘previous’ pointer?

Ans:

Enforcing a twice-linked list without a former pointer requires an indispensable system to cut the List backwards. One similar system involves using a mound to flashback the path taken during forward traversal. Still, a further space-effective approach is to render the former pointer within the coming pointer using an XOR operation. This fashion, known as XOR linked List or memory-effective twice linked List, stores the XOR of the former and coming node addresses in the place of the coming pointer.

33. Explain how one would describe a circle in a linked list and determine its length.

Ans:

• Detecting a circle in a linked list and determining its length can be fulfilled using Floyd’s Cycle-Chancing Algorithm, also known as the tortoise and the hare algorithm.
• This system involves two pointers that cut the List at different pets( one moves two ways at a time, the other one step). Still, these pointers will ultimately meet within the circle if a circle exists.
• Once the meeting point is set up, keep one pointer stationary and move the other around the circle until it returns to the meeting point, counting the number of steps it takes to complete the circuit.
• This count represents the circle’s length. The time complexity of detecting the circle is O( n), and determining its length is O( k), where n is the number of bumps outside the circle and k is the number of bumps in the circle.

34. What steps are needed to implement an LRU (Least Recently Used) cache using a linked list?

Ans:

An LRU cache can be efficiently enforced using a combination of a twice-linked list and a hash chart. The twice-linked List tracks the recency of element operation, with the most lately used particulars near the head and the least lately used particulars near the tail. The hash chart, on the other hand, provides O( 1) access time to cache particulars by storing crucial-value dyads where the key is the cache item key, and the value is the pointer to the corresponding node in the linked List.

35. Discuss the trade-offs between using an array and a linked list for enforcing a line.

Ans:

Choosing between an array and a linked list involves trade-offs. Arrays provide constant-time access to elements, making operations like indexing efficient, but they have fixed sizes (unless using dynamic arrays like ArrayList in Java), which can require costly resizing. Enqueue and dequeue operations in arrays are less efficient due to element shifting. In contrast, linked lists offer dynamic resizing and allow O(1) time for enqueue (insert at tail) and dequeue (remove from head) operations if both head and tail references are maintained.

36. How will you represent a linked list in a graphical view?

Ans:

To represent a linked list in a graphical view, you generally draw a series of bumps( frequently depicted as blocks or circles) connected by arrows that point from one node to the next. Each node is divided into two corridors: the data section, which stores the value of the node, and the pointer section, which holds the address of the coming node in the sequence. The final node’s pointer points to a null value, indicating the end of the List.

37. How many types of Linked Lists live?

Ans:

• There are three main types of linked lists: independently linked lists, twice-linked lists, and indirectly linked lists. 
• Independently linked lists contain bumps that point to the coming node in the sequence, with the last node pointing to null. 
• Twice-linked lists have bumps with two pointers, one pointing to the coming node and one to the former, allowing bidirectional traversal. 
• Indirectly linked lists are a variation where the List’s last node points back to the first node, creating a circle. Each type serves different purposes, offering various advantages in terms of traversal, insertion, and omission edge

38. How numerous pointers are necessary to apply a simple Linked List?

Ans:

In a simple, independently linked list, only one pointer is necessary for each node. This pointer links the current node to the next node in the sequence. The simplicity of having just one pointer per node makes operations like insertion and omission straightforward, as you only need to acclimate a single link at a time. Still, this also means that traversal is unidirectional, from the head of the List to the end, since there’s no backward link to former bumps.

39. What do you understand about traversal in linked lists?

Ans:

Traversal in linked lists is an abecedarian operation where each node is visited successionally, starting from the head and moving towards the last node, which points to null. During traversal, operations similar to searching for a value, modifying a node, or publishing the List’s contents can be performed. The process relies on the pointers between bumps to move from one node to the next. Traversal effectiveness is critical for numerous linked list operations, as the time complexity for operations frequently depends on the capability to snappily and effectively cut the List.

40. Mention many operations of Linked Lists.

Ans:

Linked lists are extensively used in computer wisdom due to their dynamic size and effective insertion and omission operations. These operations include enforcing other data structures like heaps, ranges, and graphs. In memory operations, linked lists can manage available memory blocks in dynamic memory allocation. They are also used in train allocation tables( FAT) for train storehouse systems, undo functionality in textbook editors, and managing the table of contents in blockchain technology.

41. Where will the free node be available while fitting a new node in a linked list?

Ans:

When fitting a new node into a linked list, the” free node” refers to the recently created node that you’re adding. This node existed singly before insertion but was yet to be linked to the List. Upon insertion, you acclimate the pointers of the being bumps( or just the head pointer if it’s the first node) to include this new node in the List. The position where this free node will be fitted can vary. It might be added in the morning, in the middle, or at the end of the List, depending on the asked position and the specific sense of the insertion operation.

42. For which title list the last node contains the null pointer?

Ans:

• In independently linked lists, the last node contains a null pointer to indicate the end of the List.
• This specific is abecedarian to the structure of independently linked lists, furnishing a clear termination point for algorithms that cut or manipulate the List. The null pointer acts as a guard, signifying that there are no further bumps to reuse, which is pivotal for operations like traversal, hunt, and insertion at the end.
• This design allows for effective successional access to elements, though it requires careful running to avoid null pointer exceptions and to rightly maintain the List’s integrity during variations.

43. What is the method to partition a linked list in Java?

Ans:

CoveringCovering a linked list in Java can be done by using a circle to move successively through each node, starting from the head. Generally, a temporary node reference, frequently called current, is used to keep track of the current node being reused. The circle continues as long as the current isn’t null, indicating that the end of the List has not been reached. Inside the circle, the current is streamlined to point to the coming node in the List ( current = current. next).

44. How do you calculate the length of a singly linked list in Java?

Ans:

• To calculate the length of an independently linked list in Java, you can initiate a count variable at 0 and also reiterate through each node of the List, incrementing the count by 1 for each node encountered until reaching the end of the List ( i.e., a null pointer).
• This process involves setting a temporary node to the head of the List and using a circle to cut the List while incrementing the count until the temporary node is null.
• The final value of the count variable will also reflect the total number of bumps in the List, effectively giving the length of the linked List.

45. How can someone display an independently linked List from first to last?

Ans:

Displaying an independently linked list from first to last in Java involves covering the List from the head node to the last node and publishing the data of each node along the way. This can be achieved by starting with a temporary node at the head of the List and using a circle to go through each node until reaching the end( null). Within the circle, the data of the current node is published, and also the temporary node reference is moved to the coming node.

46. What drawbacks does the linked List have?

Ans:

• Some downsides of using linked lists include increased memory operation due to storing pointers with each element, slower access time compared to arrays because elements aren’t conterminous in memory, and implicit increased complexity in law that manipulates linked lists, especially for newcomers. 
• Also, linked lists can lead to hamstrung memory operations and cache performance compared to array-ground structures, as bumps are frequently stoutly allocated across distant memory locales, hindering the prefetching strategies of ultramodern processors.

47. Mention some interfaces enforced by Linked List in Java.

Ans:

• In Java, the LinkedList class implements several interfaces, furnishing a wide range of functionality. These interfaces include List, which allows the LinkedList to be used as a dynamic array; Deque, enabling it to serve as a double-concluded line; and Queue, allowing it to act as a first-in-first-eschewal ( FIFO) line.
• Through these interfaces, LinkedList supports operations for mound, line, and deque, making it an adaptable data structure for various programming scripts.
• The perpetuation of these interfaces ensures that LinkedList can be seamlessly integrated into Java’s collection frame, using polymorphism for flexible law design.

48. What are fixed linked lists, and how do they work?

Ans:

Fixed linked lists are a variation of the standard linked List, where the maximum size of the List is destined and remains constant throughout the List’s continuance. Unlike dynamically linked lists, which can grow or shrink as bumps are added or removed, fixed linked lists have a set capacity, making them analogous to arrays in terms of fixed size but still maintaining the linked structure of bumps. This approach is helpful in surroundings with limited memory or where the maximum size of the List can be known in advance, reducing the outflow of dynamic memory allocation.

49. Explain how Python’s coming pointer workshop?

Ans:

Python’s” coming” pointer conception in the environment of linked lists doesn’t live in the same way as in lower-position languages like C or C, where pointers are unequivocal. In Python, linked list bumps generally contain a reference to the coming node. This is achieved using a class trait that refers to the coming node object. When enforcing a linked list in Python, you would generally define a node class with a trait(e.g., self. next) to hold this reference.

50. What’s the purpose of the display part in a linked list?

Ans:

• The display part of a linked list, frequently enforced as a system within the linked list class, is designed to visually present the List’s contents to the user. It iterates through each node, starting from the head, and prints out or returns the values stored in the bumps.
• This functionality is pivotal for debugging, testing, or any situation where viewing the List’s data in a mortal-readable form is necessary.
• The display system enhances the usability of the linked List, furnishing a straightforward way to corroborate the structure and contents of the List at any point in its manipulation.

51. How may one define a constructor for an element’s value in an indirectly linked list?

Ans:

In an indirectly linked list, defining a constructor for an element’s value involves initializing the node with the given value and setting its coming pointer to point to itself originally. This tone-representing setup is crucial for an indirect linked list’s node, especially for the singular node script. In Python, this can be achieved by defining an init system in the Node class that takes a value as an argument and sets the self. Value to this argument and self. Next to tone, establish the indirect reference. When further bumps are added, the self.

52. To what end does Python’s public void function serve?

Ans:

Python doesn’t have a” public void” function analogous to languages like Java or #. In Python, functions are defined using the def keyword, and all functions are public by dereliction, as Python doesn’t apply access modifiers like private, defended, or public. The return type isn’t explicitly stated in Python function delineations; a function without a return statement implicitly returns None, which is analogous to the” void” return type in other languages.

53. What’s the purpose of breaking boxes into separate boxes in a linked list?

Ans:

Breaking boxes into separate boxes in a linked list is a tropical way of describing the division of data into bumps, where each” box” ( node) contains a portion of the data( value) and a reference( pointer) to the coming box( node). This division enables the dynamic nature of linked lists, allowing for effective insertions and elisions. By separating data into bumps, linked lists can fluently add or remove elements without the need for conterminous memory space, as needed by arrays.

54. What’s the significance of head and tail pointers in linked lists?

Ans:

• The head and tail pointers in a linked list hold significant significance as they mark the starting and ending points of the List independently.
• The head pointer is pivotal for penetrating the List; without it, there would be no entry point to begin operations like traversal, insertion in the morning, or searching, making the List basically inapproachable.
• While not always necessary( especially in independently linked lists), the tail pointer is inestimable in twice-linked lists and indirectly linked lists for effective insertions at the end of the List and for performing operations that require penetrating the last element snappily. 

55. How can a new linked list be produced and initialized with a size of 0?

Ans:

To produce a new linked list and initialize it with a size of 0, you basically define a linked list structure with head( and conceivably tail) pointers and set these pointers to null.

This structure signifies an empty linked list where size tracks the number of elements. Originally, since there were no elements, the size was 0, and both the head and tail( if used) were pointed to null, meaning there were no bumps in the List.

56. What’s the position of the head node in a linked list when moving forward?

Ans:

In a linked list, the position of the head node is always on the morning of the List when moving forward. It acts as the anchor point for the List, furnishing the original access to the linked structure. Anyhow, regardless of the List’s size, the head node’s position remains constant; it’s the starting point for any traversal, insertion, or omission operation on the morning of the List. This harmonious positioning ensures a dependable entry point to the List and is abecedarian for repeating over or manipulating the linked List’s contents.

57. Which are the direct data structures?

Ans:

Linear data structures are those in which elements are arranged in a successional order, where each element is connected to its former and coming element in a single position. Common exemplifications include arrays, heaps, ranges, and linked lists. In these structures, data elements are organized linearly, allowing straightforward traversal and access operations. Arrays allow direct indexing, heaps and ranges provide LIFO and FIFO access respectively, and linked lists support dynamic memory allocation with linked elements.

58. How can a double tree be converted into a twice-linked list?

Ans:

• Converting a double tree into a twice-linked list involves reorganizing the tree bumps so that they follow the twice-linked list parcels. Each node has a pointer to both the former and coming bumps.
• This conversion can be done in-place ( if variable) using an in-order traversal. During traversal, former and current bumps are acclimated to link to each other independently as coming and former bumps. The left child pointer can act as the former pointer and the right child as the coming pointer. 
• Care is taken to handle the head and tail bumps of the performing List, especially ensuring the head former is null, and the tail’s coming is null, thereby completing the metamorphosis.

59. Why is merge sort a more option than quicksort for linked lists?

Ans:

Combine sort is frequently considered a better option than quicksort for sorting linked lists due to its essential stability and effectiveness in handling linked data structures. Unlike arrays, linked lists can be resolved and intermingled without taking redundant space for the merge operations, making merge kind naturally effective for lists. Also, combined sort guarantees a stable kind and a harmonious time complexity of O( n log n), anyhow of the input order.

60. Prize all leaves from a double Tree into a twice-linked list ( DLL).

Ans:

Rooting all leaves from a double tree into a twice-linked list ( DLL) involves covering the double tree and disassociating the splint bumps from their parents, as well as linking these leaves together in a DLL. The process generally uses a depth-first hunt( DFS) strategy, recursively visiting each node and checking if it’s a splint. When a splint node is encountered, it’s removed from the tree and added to the DLL. This operation alters the original tree structure by removing the splint bumps.

61. Construct a twice-linked list out of a ternary tree.

Ans:

To convert a ternary tree into a doubly linked list (DLL), you need to traverse the tree and create DLL nodes corresponding to each tree node. Choose a traversal order (e.g., pre-order, in-order, or post-order) and process each node to create DLL nodes. Since each tree node has up to three children, decide how to represent these children in the DLL while preserving some logical order or structural information. This process involves mapping the tree structure to the DLL, maintaining an appropriate sequence and structure in the list.

62. Which processes are involved in levelling a linked list?

Ans:

• Levelling a linked list, especially when the List contains nested lists( i.e., a node could point to another linked list), involves two primary processes: traversal and incorporating.
• The traversal process navigates through the List, relating any nested structures that need to be smoothed. The coupling process also concatenates these nested lists with the main List, ensuring that all elements are in a single, direct sequence.
• This operation may bear recursive approaches or iterative styles with supplementary data structures like heaps to effectively handle the nesting, aiming to maintain the original order while achieving a fully flat structure.

63. What’s the time complexity to cut all the elements in an independently Linked List?

Ans:

The time complexity to cut all the elements in an independently Linked List is O( n), where n is the number of bumps in the List. This is because each node in the List is visited exactly formerly, taking a single pass from the head of the List to the end. The traversal time grows linearly with the number of bumps as each node’s pointer directs to the coming node, making the process straightforward but directly dependent on the List’s size.

64. What’s the time complexity to fit an element at any position in an independently LinkedList?

Ans:

The time complexity to fit an element at any position in an independently Linked List is O( n) in the worst case. This is because, in the worst script, fitting an element at a specific position requires covering the List from the head up to the point of insertion to detect the correct position. An insertion at the end of the List or near the end means visiting nearly every node, making the operation linearly dependent on the size of the List.

65. What’s the time complexity to cancel an element at any position in an independently Linked List?

Ans:

The time complexity to cancel an element at any position in an independently Linked List is also O( n) in the worst case. Analogous to insertion, deleting an element may bear covering the List to find the node and annotate the one to be deleted so that its pointer can be acclimated to bypass the deleted node. The necessity to detect the former node means that in the worst case( deleting the last node or a node near the end), the operation is direct with respect to the number of bumps in the List.

66. What’s the time complexity to insulate odd and indeed bumps in a LinkedList?

Ans:

The time complexity to insulate odd and indeed bumps in a linked list is O( n), where n is the number of bumps in the List. This process involves repeating through the linked List formerly, rearranging the bumps as you go grounded on their odd or indeed values. No fresh passes over the List are needed, and since each node is visited exactly formerly during the isolation process, the operation completes indirect time.

67. What’s the time complexity to find the kth node from the end in a LinkedList?

Ans:

• Chancing the kth node from the end in a linked list has a time complexity of O( n), where n is the total number of bumps in the List. This can be achieved by using the two-pointer fashion, where one pointer starts moving only after the other pointer has made its way.
• Once the leading pointer reaches the end of the List, the running pointer will be at the kth node from the end. This system requires only a single pass through the List, making it an effective result that scales linearly with its size.

68. What’s the time complexity to describe a circle in a LinkedIn list?

Ans:

Detecting a circle in a linked list can be fulfilled with a time complexity of O( n) using Floyd’s Cycle-Chancing Algorithm, also known as the tortoise and the hare algorithm. This approach involves two pointers moving at different pets( one faster than the other). Still, they will ultimately meet inside the circle If there’s a circle. Since each step of the algorithm processes a constant number of bumps and the number of ways is commensurable to the number of bumps in the List, the total time complexity remains direct in the size of the input list.

69. What’s the time complexity to check if a linked list is palindrome?

Ans:

Checking if a linked list is a palindrome can be done with a time complexity of O( n), where n is the number of bumps in the List. This generally involves reversing the alternate half of the List and comparing it with the first half. The process of changing the middle, reversing, and comparing takes direct time since each of these ways involves covering portions of the List only formerly. This ensures that the overall process remains effective, allowing for palindrome checks to be performed fairly snappily indeed as the size of the List increases.

70. What’s the time complexity required to find a crossroad point in a shaped list?

Ans:

Chancing the crossroad point in a Y-shaped list has a time complexity of O( n m), where n and m are the lengths of the two linked lists. This is achieved by first determining the lengths of both lists and also aligning them at the same starting point from the tail by skipping the original bumps of the longer List. Once both pointers are aligned, they move in tandem until they find the crossroad point. This system requires covering each List at most once, making the process effective and direct in terms of the total number of bumps in both lists.

71. Is it possible to produce a twice-linked list using only one pointer with every node?

Ans:

• Creating a twice-linked list using only one pointer per node is possible through the XOR linked List, a complex and less common perpetration.
• In an XOR-linked list, rather than storing factual memory addresses, each node stores the XOR of addresses of the former and coming bumps.
• This fashion allows navigation in both directions by calculating the missing address using the XOR of the given address and the stored XOR value. Still, this approach requires fresh bitwise operations for traversal and can complicate law, making remedying further gruelling.
•  It also sacrifices readability and portability for memory effectiveness, making it a technical result rather than a common practice.

72. What’s a temporary variable in the environment of linked lists?

Ans:

In the environment of linked lists, a temporary variable is frequently used as a placeholder or coadjutor during various operations like insertion, omission, or switching of bumps. For illustration, when switching two bumps, a temporary variable may hold the data or the address of a node to help lose access to it during the exchange process. Temporary variables are pivotal for maintaining integrity and order within the List during variations, ensuring that operations can be performed without inadvertently corrupting the List’s structure or losing data.

73. What’s scrap collection in the linked List?

Ans:

Garbage collection in the environment of linked lists refers to the automatic reclaiming of memory allocated for bumps that are no longer in use or accessible from the List. In languages like Java or Python, where scrap collection is erected-, once a node is removed from a linked list, and no references to it remain, the scrap collector ultimately frees the memory it enthralled.

74. Reverse A Sublist Of Linked List?

Ans:

• Reversing a sublist of a linked list involves reordering a portion of the List while keeping the rest of the List complete. This can be achieved by first locating the launch and end of the sublist and also iteratively reversing the pointers within this range.
• Many fresh pointers are generally used to keep track of the bumps just ahead and just after the sublist, ensuring a smooth reconnection with a non-reversed corridor of the List.
• This operation requires careful pointer manipulation to ensure the integrity of the List is maintained while the sublist is reversed.

75. Run Length Decoding in Linked List?

Ans:

Run Length Decoding in a linked list involves expanding a compressed list, where each node contains a character and a count, into a completely expanded interpretation where each character appears successionally in the List as numerous times as indicated by its count. This process entails covering the original List and, for each node, creating multiple new bumps with the same character value grounded on the count, also linking these bumps meetly to form the expanded List.

76. Exchange bumps in a linked list without switching data?

Ans:

Switching bumps in a linked list without switching data involves changing the bumps’ links rather than their content. This is particularly useful when the data part of the bumps is large or complex. The process requires conforming the pointers of the bumps, annotating those being shifted, and the pointers of the bumps being shifted themselves to reflect their new positions. Care must be taken to handle cases where the bumps are conterminous or at the head of the List, as these scripts bear special consideration to avoid breaking the List.

77. What fields does a twice twice-linked list comprise?

Ans:

• A twice-linked list comprises three main fields in each node: data, prev, and next. The data field stores the value contained in the node, while the previous and coming are pointers.
• The prev pointer links to the former node in the List, and the coming pointer links to the coming node. This structure allows for effective bidirectional traversal of the List.
• The head node’s previous pointer and the tail node’s coming pointer are generally set to null, indicating the morning and end of the List independently.
• The addition of both prev and coming pointers provides inflexibility in manipulation and traversal, making operations like insertion and omission more effective from any position within the List.

78. How to Convert a Double Tree into the Twisted Linked List?

Ans:

Converting a double tree into a twice-linked list generally involves an in-order traversal to ensure that the elements are sorted according to their values in the double tree. The process involves recursively visiting the left child, recycling the current node, and also visiting the right child. During each visit, the current node is modified to link it with the preliminarily visited node( acting as its former node in the List) and the coming visited node( as it is coming). This revision is done by conforming the left and right pointers of the double tree bumps to serve as the former and coming pointers in the twice-linked List.

79. What’s the difference between a train structure and a storehouse structure?

Ans:

Train Structure:

• Linear and Sequential: This is comparable to data structures like linked lists, in which elements are connected sequentially, one after the other, like cars in a train; each element points to the next and occasionally the previous, similar to the coupling between train cars;
• Dynamic Size: These structures can grow or shrink dynamically, adding or removing elements as needed during runtime, just as additional cars can be added or removed from a train.

Storehouse structure:

• Random Access: This is comparable to data structures like arrays or hash tables, where data can be accessed directly via indices or keys, like obtaining items from specific locations in a warehouse.
• Less Dynamic or Fixed Size: Although contemporary programming languages support dynamic arrays, an array’s size is often fixed, akin to a warehouse’s capacity.

80. How information is crescively organized, enabling effective data reclamation and storehouse?

Ans:

Again, storehouse structure refers to the way data is organized and stored in memory, either temporarily during program prosecution or permanently on storehouse bias. It encompasses the arrangement of data in memory, the algorithms used for data access, and the overall operation of data spaces, affecting performance and data handling effectiveness.

81. What’s a multidimensional array?

Ans:

A multidimensional array stores and accesses data in more than one dimension. For example, a 2D array, resembling a grid or matrix with rows and columns, is used for complex data representations such as spatial grids, tables, and matrices. Extending to higher dimensions, like 3D arrays for volumetric data, these arrays are essential in scientific computing, data analysis, and tasks requiring structured data representation.

82. How are the elements of a 2D array stored in the memory?

Ans:

• The elements of a 2D array are stored in memory either in row-major order or column-major order, depending on the language and its memory allocation pattern. In row-major order, all the elements of the first row are stored contiguously, followed by the elements of the alternate row, and so on.
• This means that elements are penetrated and stored linearly according to their logical arrangement in rows, making it effective to pierce row elements successionally.
• The conterminous allocation helps in optimizing memory operations and access patterns, particularly for operations that involve surveying rows, as it benefits from spatial position, enhancing cache application.

83. Are linked lists considered direct or non-linear Data Structures?

Ans:

Linked lists are considered direct data structures because they successfully organize data. Despite their non-contiguous memory allocation, the elements( bumps) in a linked list are linked successionally by pointers, ensuring a direct traversal order. Each node points to the coming node, establishing a single, unidirectional path from the morning to the end of the List. This characteristic aligns with the description of direct data structures, where elements are arranged in a direct sequence.

84. What is the process to source all elements in a one-dimensional array?

Ans:

To source all of the elements in a one-dimensional array, you generally use a circle that iterates from the first element at indicator 0 to the last element at indicator length- 1 of the array. In each replication of the circle, you pierce the element at the current indicator. This approach is language-agnostic and can be enforced in various programming languages with syntax acclimations. For case, in Python, you can use a circle or list appreciation, and in C or Java, you traditionally use a circle with an indicator variable that supplements until it reaches the array’s length.

85. Why do we need to do an algorithm analysis?

Ans:

• Algorithm analysis is essential to understand the effectiveness and performance of algorithms under different conditions. It helps in determining the computational complexity in terms of time( how long an algorithm takes to run) and space( how important memory an algorithm uses).
• By assaying algorithms before enforcing them, we can predict their geste on various input sizes and choose the most applicable bone for a given problem. This is pivotal in software development for making informed opinions that impact the scalability, effectiveness, and overall performance of operations.
• Algorithm analysis ensures that the named algorithm optimally utilizes coffers, furnishing a balance between speed and memory operation.

86. Where are heaps used?

Ans:

• Heaps are used in several areas within computer wisdom and programming due to their LIFO( Last In, First Out) nature.
• They’re pivotal in managing function calls and recursion in programming languages, where each call is placed on a mound and removed upon completion. 
• Heaps grease undo mechanisms in textbook editors, where each action is pushed onto the mound and popped to revert conduct.
• They’re also used in algorithmic problems like assessing expressions, parsing syntax in compilers, and managing cybersurfer history, where the most recent runner visited is the first to be redefined.

87. What’s an algorithm?

Ans:

An algorithm is a finite sequence of well-defined computer-implementable instructions used to break a class of problems or perform a calculation. Algorithms are:

• The backbone of computer wisdom and programming.
• Furnishing a clear way for processing data.
• Making computations.
• Automating decision-making processes.

They range from simple procedures like sorting and searching to complex operations like data contraction and encryption.

88. How does the Selection sort work?

Ans:

The selection kind is a straightforward sorting algorithm based on the comparison that separates an input list into two sections: the sorted portion at the start and the unsorted portion at the end. The elements are all in the unsorted half, whereas the sorted part is initially empty. The unsorted part’s lowest (or largest, depending on the sorting order) element is continuously chosen by the algorithm, which then trades it for the unsorted element farthest to the left and shifts the border between the sorted and unsorted corridors by one element.

89. Do dynamic memory allocations help in managing data?

Ans:

• Dynamic memory allocation plays a pivotal role in managing data by furnishing inflexibility in the use and operation of memory according to programs’ runtime conditions.
• This capability is particularly precious in situations where the quantum of data isn’t known in advance. With dynamic memory allocation, programs can request free memory on the fly, optimizing the use of available memory coffers. This leads to more effective memory operation and can significantly reduce a program’s static memory footprint. 
• Also, data structures like linked lists, trees, and graphs greatly benefit from dynamic allocation, allowing them to grow or shrink as demanded during prosecution.

90. List some operations of multilinked structures.

Ans:

Multilinked structures, which are data structures with bumps that have multiple pointers connecting various elements, find operations in several complex and advanced computing scripts. For illustration, they’re used in spatial data structures like quadtrees and octrees, which are pivotal for efficiently managing two- dimensional and three-dimensional spatial queries in computer plates, geographic information systems( Civilians), and collision discovery in gaming. Multilinked structures also bolster advanced database indexing mechanisms, similar to B- trees and B trees, which give effective access and revision operations for large databases.