35+ [REAL-TIME] Data Structure Interview Questions and Answers

Last updated on 04th Jul 2020, Blog, Interview Questions

A data structure is a specialized format for organizing, processing, and storing data efficiently. It enables quick access and modification, making it vital for algorithm design and managing large data sets. Common examples include arrays, linked lists, stacks, queues, trees, and graphs. Mastery of data structures is key to optimizing performance and solving complex computational problems effectively.

1. Explain what data structure is.

Ans:

Data structure refers to the organization and storage of data in computers. It enables efficient access and manipulation of data. Hash tables, trees, graphs, linked lists, and arrays are a few examples. Data structures are essential in computer science for solving diverse computational problems. Effective utilization of data structures optimizes algorithms and enhances program performance. Depending on their arrangement, data structures can be linear or hierarchical.

2. Describe the types of Data Structures.

Ans:

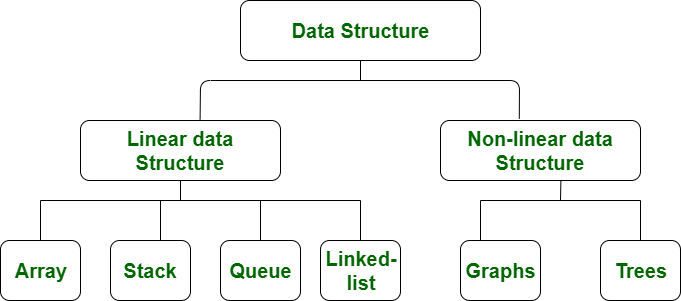
• Data structures are broadly classified into linear and nonlinear categories.
• Linear structures include arrays, linked lists, stacks, and queues.
• Nonlinear structures encompass trees and graphs.
• Linear structures organize elements sequentially, while nonlinear structures represent data hierarchically.
• Each type serves specific purposes and entails distinct operations.

3. What is a Linear Data Structure? Name a few examples.

Ans:

• Element arrangement in linear data structures is sequential.
• Examples comprise arrays, linked lists, stacks, and queues.
• Elements are kept in arrays in a continuous block of memory.
• Linked lists employ pointers to connect individual elements.
• Stacks adhere to the Last In, First Out (LIFO) principle.
• Queues follow the First In, First Out (FIFO) principle.

4. What are some applications of Data Structures? 

Ans:

• Data structures find applications across diverse domains.
• They are fundamental in database management systems for efficient data handling.
• Algorithms for searching, sorting, and graph traversal heavily rely on data structures.
• Networking protocols, file systems, and compilers utilize data structures extensively.
• Operating systems manage memory resources efficiently using data structures.

5. What are the basic operations performed on various data structures?

Ans:

Basic operations include insertion, deletion, traversal, searching, and sorting. Insertion involves adding elements to the data structure. Deletion removes elements from the structure. Traversal visits each element in a specific order. Searching determines the presence and location of elements. Sorting arranges elements in a defined sequence.

6. Explain what is a linked list?

Ans:

Linked lists are linear structures comprising nodes linked via pointers. Every node has information and a pointer to the node after it. Unlike arrays, linked lists do not require contiguous memory allocation. They support dynamic memory management, accommodating growth or reduction. Common operations include insertion, deletion, traversal, and searching. Linked lists exist in various forms, such as singly linked, doubly linked, and circular linked lists.

7. List out the areas where the data structure is applied.

Ans:

• Data structures are used in databases for efficient data storage and retrieval.
• They are applied in networking for routing algorithms and packet switching.
• Operating systems utilize data structures for managing processes, files, and memory.
• Compilers and interpreters employ data structures for parsing and code optimization.

8. What is the primary distinction between a POP and a PUSH?

Ans:

Operation	PUSH	POP
Definition	Adds an element to the top of a stack	Removes the top element from a stack
Action	Increases the stack size by one	Decreases the stack size by one
Effect	New element becomes the top of the stack	Top element is removed and the next element becomes the top
Usage	Insertion of data	Removal of data
Return Value	Generally none or the inserted element	The element that is removed

9. Explain the terminology LIFO.

Ans:

LIFO stands for Last-In, First-Out. It refers to the principle that the last element inserted into a data structure is the first one to be removed. LIFO is commonly associated with stacks, where elements are pushed onto and popped off the top of the stack. It ensures that the most recent item added to the stack is the first to be removed, similar to a stack of plates. LIFO is used in various applications, such as function calls, undo mechanisms and expression evaluation.

10. Explain what is a binary tree?

Ans:

A binary tree is a node-based hierarchical data structure. Each node can have at most two children: the left child and the right child. The topmost node is called the root node, and it is the starting point for traversing the tree. Binary trees are commonly used in computer science for various applications, such as binary search trees and expression trees. When properly balanced, they provide efficient search, insertion, and deletion operations. Binary trees facilitate the organization and retrieval of data in a structured manner.

11. Define what a stack is.

Ans:

• A stack embodies a linear data structure adhering to the Last In, First Out (LIFO) principle.
• Its top end facilitates element addition and removal.
• Notable operations include push (for addition) and pop (for removal).
• Widely employed in algorithms and applications like function calls and expression evaluation.
• Stack operations efficiently handle insertions and deletions yet only allow access to the topmost element.

12. What are infixes, prefixes, and postfixes in data structure?

Ans:

• Infix notation is the conventional mathematical notation, e.g., A + B.
• Prefix notation places the operator before the operands, e.g., + A B.
• Postfix notation places the operator after the operands, e.g., A B +.

13. What is FIFO?

Ans:

FIFO, denoting First In, First Out, is a tenet governing queue data structures. Elements ingress at the rear and egress from the front.FIFO ensures the initial element inserted garners the initial removal. In contrast to stacks’ Last In, First Out (LIFO) sequence, queues adhere to FIFO. They are commonly deployed in CPU scheduling and network packet routing scenarios.FIFO endorses orderly element processing.

14. Describe merge sort and its applications.

Ans:

• Merge sort epitomizes a divide-and-conquer sorting algorithm.
• It segments the input array into smaller, sorted sub-arrays.
• These sub-arrays are subsequently merged to yield the final sorted array.
• Merge sort invariably boasts a time complexity of O(n log n) across all scenarios.
• Valued for its efficacy in sorting extensive datasets.
• Renowned for stability and applicability to linked lists.

15. How does variable declaration affect memory allocation?

Ans:

Upon variable declaration, memory allocation is initiated to accommodate its value. The quantum of allocated memory hinges on the variable’s data type. For instance, an integer variable typically consumes 4 bytes. If multiple variables are declared, memory allocation ensues for each. Allocation transpires either at compile-time or runtime, contingent on the variable type. Memory allocation wields ramifications on memory utilization and performance.

16. Define the advantages and disadvantages of the heap compared to a stack.

Ans:

• The heap embodies dynamically allocated memory catering to runtime variable creation.
• It facilitates dynamic memory allocation and deallocation.
• Despite its versatility, heap memory is comparatively slower due to dynamic allocation overhead.
• Unlike the stack, heap memory isn’t bound by size constraints.
• However, mismanagement can precipitate memory leaks and fragmentation.

17. Explain how new data can be inserted into the tree.

Ans:

To insert new data into a tree, traverse the tree to locate the suitable position based on the data value and tree rules. Once found, please create a new node to hold the data and insert it into the tree as per insertion rules. This may involve adjusting pointers and restructuring the tree to maintain its integrity. After insertion, the tree might require rebalancing for optimal performance.

18. Explain a little bit about the dynamic data structure.

Ans:

Dynamic data structures adjust their size during program execution. Examples include linked lists, trees, heaps, and hash tables. They utilize dynamic memory allocation for flexible memory management. While efficient for handling fluctuating data, careful memory management is crucial to prevent issues like memory leaks and fragmentation.

19. Define what is an array?

Ans:

• An array comprises elements of the same data type stored contiguously in memory.
• Elements are accessed via an index indicating their position.
• Arrays have a fixed size set during compilation.
• They offer constant-time access but lack flexibility in size.
• Arrays are adept at storing and manipulating data efficiently, supporting operations like insertion, deletion, searching, and sorting.

20. Explain what is a dequeue?

Ans:

A dequeue, or double-ended queue, enables the insertion and deletion of elements from both ends. It amalgamates features of stacks and queues, offering LIFO and FIFO operations. Supporting operations like insertFront, insertRear, deleteFront, and deleteRear it’s implementable using arrays or linked lists. Dequeues are versatile, ideal for scenarios necessitating efficient element addition and removal from both ends, such as job scheduling and task management.

21. Explain the process of how a selection sort works.

Ans:

• Selection sort works by iteratively identifying the minimum element from the unsorted portion and swapping it with the element at the current position.
• Until the entire array is sorted, this process is repeated.
• Each iteration ensures that the smallest element is placed at the beginning of the unsorted portion.
• While selection sort is simple, it’s inefficient for large datasets due to its time complexity of O(n^2).

22. What is the difference between a stack and a queue?

Ans:

• Stacks operate based on the Last In, First Out (LIFO) principle, where the most recently added element is the first one removed.
• In contrast, queues follow the First In, First Out (FIFO) principle, where the element added first is the first to be removed.
• Stacks find applications in managing function calls, expression evaluation, and backtracking.
• Queues are commonly used for task scheduling, resource management, and implementing breadth-first search algorithms.

23. Explain the concept of a hash table and its applications.

Ans:

Hash tables store key-value pairs and utilize a hash function to map keys to indices in an array, enabling efficient insertion, deletion, and retrieval. Widely employed in database indexing, caching, and symbol tables in compilers, hash tables provide constant-time access in ideal scenarios. However, their performance may degrade to linear time in worst-case scenarios due to collisions, which are resolved using chaining or open-addressing techniques. Despite potential performance issues, hash tables are invaluable for applications requiring fast data access and manipulation.

24. How does a binary search tree differ from a binary tree?

Ans:

• Binary trees are hierarchical structures where each node can have up to two children: left and right.
• Binary search trees (BSTs) are a type of binary tree with specific ordering rules: the left child contains values less than the parent, and the right child contains greater values.
• BSTs support efficient searching, insertion, and deletion operations with an average time complexity of O(log n).
• While regular binary trees lack a specific ordering among elements, BSTs maintain order, making them suitable for search and sorting tasks.

25. Describe the process of traversing a binary tree.

Ans:

Traversing a binary tree involves visiting each node following a specific order. Preorder traversal visits nodes in the order: root, left subtree, right subtree. In order traversal visits nodes in the order left subtree, root, right subtree. The nodes visited by postorder traversal are the root, left subtree, and right subtree. Traversal algorithms can be implemented recursively or iteratively using stacks or queues. Each traversal order has unique applications, such as expression evaluation, sorting, and constructing expression trees.

26. What are the advantages of using a linked list over an array?

Ans:

• Linked lists provide dynamic memory allocation, facilitating efficient insertion and deletion operations without shifting elements.
• They dynamically adjust in size, unlike arrays with fixed sizes.
• Linked lists mitigate memory fragmentation issues by allocating memory as needed.
• Operations like inserting and deleting elements in the middle or beginning of a linked list are constant-time.
• Linked lists serve well in implementing stacks, queues, and adjacency lists for graphs, demonstrating their versatility in various data structures and algorithms.

27. Explain the concept of recursion and its relation to data structures.

Ans:

Recursion involves a function calling itself to solve smaller instances of a problem, often used in data structures like trees and graphs. It simplifies complex problems by breaking them down into smaller, more manageable subproblems. Recursion utilizes a call stack to keep track of function calls, which is essential for traversing data structures recursively. It’s a powerful technique for implementing algorithms such as depth-first search and divide-and-conquer.

28. What are the characteristics of a priority queue?

Ans:

A data structure with a priority assigned to each entry is called a priority queue. It supports two primary operations: insertion and deletion of the highest priority element. Priority queues can be implemented using various underlying data structures like heaps or balanced trees. They ensure that the highest priority element is always removed first, making them useful in applications such as scheduling and task management.

29. How does a graph data structure differ from a tree?

Ans:

A graph is a collection of nodes connected by edges, allowing for more complex relationships between nodes compared to a tree. Graphs can have cycles and multiple paths between nodes, while trees are acyclic and have a hierarchical structure. Graphs are more general and versatile, supporting various algorithms like shortest path and minimum spanning tree, whereas trees have specific traversal and manipulation algorithms.

30. Explain the concept of hashing and collision resolution techniques.

Ans:

• Hashing is a technique used to map data of arbitrary size to fixed-size values, known as hash codes, using a hash function. 
• Collision occurs when two distinct inputs produce the same hash code. 
• Chaining involves storing multiple elements with the same hash code in a linked list, while open addressing finds alternative locations within the hash table for collided elements.

31. What is the time complexity of various operations in a binary search tree?

Ans:

• Insertion: O(log n)
• Deletion: O(log n)
• Searching: O(log n)
• Traversal: O(n)
• Finding minimum/maximum: O(log n)
• Finding successor/predecessor: O(log n)

32. Describe the concept of a doubly linked list and its advantages.

Ans:

A doubly linked list has nodes with pointers to both the previous and next nodes. It efficiently allows traversal in both forward and backward directions. It supports operations like insertion and deletion at both ends in O(1) time. A doubly linked list offers more flexibility compared to a singly linked list. However, due to the additional pointers in each node, it requires more memory. Moreover, it provides faster removal of nodes compared to a singly linked list.

33. How does a queue differ from a dequeue?

Ans:

• Queue: Follows the FIFO (First-In-First-Out) principle; elements are inserted from the rear and removed from the front.
• Dequeue (Double-Ended Queue): Supports insertion and deletion operations at both ends.
• Queue has only two ends, while dequeue has front and rear ends.
• Dequeue can function as both a queue and a stack.
• Queue has simpler operations compared to dequeue.
• Dequeue provides more flexibility in handling data.

34. Explain the concept of dynamic memory allocation in data structures.

Ans:

Dynamic memory allocation involves allocating memory at runtime rather than at compile time. This flexibility allows data structures to adjust to changing requirements by allocating memory as needed during program execution. Common functions such as malloc(), calloc(), and realloc() in languages like C and C++ are used to dynamically allocate and resize memory, enabling efficient management of memory resources based on program demands.

35. What are the different types of sorting algorithms? Provide examples.

Ans:

• Some examples of sorting algorithms include Bubble Sort, Selection Sort, Insertion Sort, Merge Sort, Quick Sort, and Heap Sort.
• These algorithms differ in their time complexity, stability, and efficiency depending on factors like input size and initial order.

36. How can you implement a stack using an array?

Ans:

• Use an array to store elements and an integer variable to keep track of the top of the stack.
• Push operation: increment the top and insert the element at the top index.
• Pop operation: decrement the top and remove the element at the top index.
• Check for stack overflow and underflow conditions.

37. Describe the process of deleting a node from a linked list.

Ans:

• Locate the node to be deleted by traversing the list.
• Adjust pointers of the previous node to bypass the node to be deleted.
• Free the memory allocated to the node being deleted.

38. What are the advantages of using a heap data structure?

Ans:

• Efficient for implementing priority queues and heap sort.
• Gives access to the maximum (or smallest) element continuously.
• Supports efficient insertion and deletion of elements.
• It can be implemented using arrays, making it memory-efficient.

39. Explain the process of balancing a binary search tree.

Ans:

Balancing a binary search tree involves ensuring that the height difference between any node’s left and right subtrees is within a certain range. This prevents the tree from becoming skewed, ensuring efficient search, insertion, and deletion operations. Common balancing techniques include rotating and reordering nodes to maintain balance.

40. What are the characteristics of a circular linked list?

Ans:

• A circular linked list has no NULL pointer; the last node points back to the first node.
• Supports both forward and backward traversal.
• Requires special handling for insertion and deletion operations.
• Suitable for applications requiring continuous looping.
• It prevents the need to traverse the entire list to reach the last node.
• Offers constant insertion and deletion at both ends.

41. What is the difference between depth-first search and breadth-first search?

Ans:

• DFS investigates each branch as far as it can go before turning around.
• BFS explores neighbors of the current vertex before moving to the next level.
• DFS uses a stack data structure for implementation.
• BFS uses a queue data structure for implementation.
• DFS is often used in solving maze problems or graph traversal.

42. Describe the process of inserting and deleting elements in a hash table.

Ans:

Insertion involves hashing the key to find the appropriate index and storing the value. Collision resolution techniques like chaining or probing handle collisions. Deletion requires finding the key and then removing the corresponding entry. For chaining, deleting involves removing the entry from the linked list. For probing, the entry can be marked as deleted or replaced with a placeholder. Both operations have an average time complexity of O(1) under ideal conditions.

43. How can you implement a priority queue using a heap?

Ans:

Priority queues maintain elements based on their priority. A heap is a suitable data structure for implementing a priority queue. Insertion in a heap involves adding the element to the end and then fixing the heap property. Deletion involves removing the root element and rearranging the heap. Heapify operations ensure that the heap maintains its properties after insertion or deletion. Heaps typically use arrays for storage and have efficient time complexities for insertion and deletion.

44. What is the difference between a binary search and a linear search?

Ans:

• Binary search operates on sorted arrays or lists.
• Linear search iterates through each element in the array sequentially.
• Binary search compares the target value with the middle element and eliminates half of the remaining elements.
• Linear search compares each element in the array until finding the target or reaching the end.
• Binary search has a time complexity of O(log n) in the average case.

45. Explain the concept of amortized analysis in data structures.

Ans:

• Amortized analysis evaluates the average time or space complexity of a sequence of operations.
• It provides a more accurate estimation of the overall performance.
• Example: Dynamic arrays use amortized analysis to show that the average time complexity of insertion is O(1).
• The amortized analysis considers both expensive and cheap operations over a series of operations.
• It helps in understanding the overall efficiency of data structures over time.

46. How do you implement a stack using a linked list?

Ans:

A stack implemented with a linked list utilizes nodes with a reference to the next node. The push operation inserts a new node at the beginning of the linked list. The pop operation removes the node at the beginning of the linked list. The top operation returns the value of the node at the beginning of the linked list. A linked list implementation provides dynamic memory allocation for stack elements. Stack operations have a time complexity of O(1) with a linked list implementation.

47. Describe the process of reversing a linked list.

Ans:

A linked list can be reversed by flipping the pointers’ orientation. Traverse the linked list, maintaining references to the current, previous, and next nodes. At each step, update the next pointer of the current node to point to the previous node. Move the pointers to the next nodes accordingly. Repeat until reaching the end of the linked list. Update the head pointer to the last node encountered, which becomes the new head.

48. What are self-balancing trees, and why are they important?

Ans:

• Self-balancing trees maintain balance to ensure efficient operations.
• Examples include AVL trees, red-black trees, and B-trees.
• Balance is essential for maintaining optimal time complexities for operations.
• Unbalanced trees may lead to skewed structures and degraded performance.
• Self-balancing mechanisms like rotations and color adjustments maintain balance during insertions and deletions.

49. Explain the concept of a trie data structure.

Ans:

A tree is a tree-like data structure used for storing strings. Each node represents a single character of the string. Trie nodes have links to child nodes corresponding to possible next characters. Trie structures efficiently support operations like prefix search and insertion. They consume memory efficiently, especially for large datasets with similar prefixes. Trie structures are commonly used in autocomplete systems, spell checkers, and dictionary implementations.

50. How does an AVL tree differ from a red-black tree?

Ans:

• Both are self-balancing binary search trees.
• AVL trees ensure balance by maintaining a balance factor for each node.
• Red-black trees use color attributes to maintain balance and ensure logarithmic height.
• AVL trees have stricter balancing rules, leading to faster lookups but potentially slower insertions and deletions.
• Red-black trees have more relaxed balancing requirements, offering faster insertion and deletion operations.

51. What is the significance of topological sorting in graphs?

Ans:

• Topological sorting orders the vertices in a directed acyclic graph (DAG) based on dependencies.
• It’s crucial in scheduling tasks or events with precedence constraints.
• Applications include project management, task scheduling, and job scheduling in compilers.
• It helps detect cycles in graphs, ensuring consistency and avoiding deadlock situations.

52. Describe the process of performing a binary search on an array.

Ans:

Binary search operates on a sorted array, dividing it into halves to find a target element. It compares the target value with the middle element and narrows down the search space. If the target is less/greater than the middle element, the search continues in the left/right subarray. The process repeats until the target is found or the search space is exhausted. It’s widely used in searching and retrieval applications like databases and sorting algorithms.

53. What are the advantages of using a doubly-ended queue?

Ans:

• A deque supports insertion and deletion operations at both ends in constant time.
• It combines the features of both stacks and queues, offering versatility.
• Deques can be used to implement more complex data structures like queues and stacks.
• They provide efficient solutions for problems requiring simultaneous insertions and removals.
• Deques facilitate bidirectional iteration, enhancing flexibility in algorithm design.

54. Explain the concept of binary heap and its operations.

Ans:

A binary heap is a complete binary tree with the heap property, where each node is less/greater than its children. It’s commonly implemented as an array, ensuring efficient memory usage. Operations include insertion, deletion, and beatification. Insertion involves adding a new element at the end and restoring the heap property. Deletion removes the root element and then restructures the heap to maintain the heap property. Heapify transforms an unordered array into a heap, typically used in heap sort and priority queues.

55. How do you handle collisions in a hash table?

Ans:

• When two or more keys hash to the same hash table index, a collision occurs.
• Techniques to handle collisions include chaining and open addressing.
• Chaining involves maintaining a linked list or other data structure at each hash table index.
• Open addressing methods probe for alternative locations to store collided keys within the table.
• Popular probing techniques include linear probing, quadratic probing, and double hashing.

56. Describe the process of tree traversal without recursion.

Ans:

• Non-recursive tree traversal can be achieved using a stack data structure.
• For in-order traversal, push left child nodes onto the stack until reaching the leftmost leaf.
• Pop nodes from the stack, process them and move to the right child if available.
• Continue doing this until every node has been visited.
• Preorder and postorder traversals follow similar principles with variations in node processing order.

57. What is the importance of binary trees in computer science?

Ans:

Binary trees are fundamental data structures used for efficient searching, sorting, and storing hierarchical data. They enable quick retrieval, insertion, and deletion operations with time complexity O(log n) in balanced trees. Binary trees serve as the foundation for various advanced data structures like binary search trees, AVL trees, and red-black trees. They are crucial in algorithm design, facilitating solutions for problems like tree traversal, dynamic programming, and graph algorithms.

58. Explain the concept of heapify in a heap data structure.

Ans:

Heapify is the process of rearranging elements in a heap to maintain the heap property. It ensures that the parent node is greater (for a max heap) or smaller (for a min-heap) than its children. Heapify is typically used during heap construction and heap deletion operations. It has a time complexity of O(log n), where n is the number of elements in the heap. Heapify involves recursively applying heapify down (or up) operations to restore the heap property.

59. How can you implement a queue using stacks?

Ans:

• To implement a queue using stacks, use two stacks: one for enqueue operations and the other for dequeue operations.
• For enqueue, push elements onto the first stack.
• For dequeue, if the second stack is empty, pop all elements from the first stack and push them onto the second stack.
• Pop from the second stack to perform dequeue operations.
• This approach maintains the FIFO (First-In-First-Out) order of the queue.

60. Describe the process of finding the lowest common ancestor in a binary tree.

Ans:

• Start from the root and recursively search for the given nodes in the left and right subtrees.
• If both nodes are found in separate subtrees, the current node is the lowest common ancestor.
• If one node is found, continue searching in the other subtree.
• If neither node is found, return null.
• The process terminates when both nodes are found in separate subtrees or when one node is found, and the other is not.

61. How do you detect a loop in a linked list?

Ans:

To detect a loop in a linked list, we use Floyd’s Tortoise and Hare algorithm. We initialize two pointers, slow and fast, which start at the head of the list. The fast pointer advances two steps at a time, while the slow pointer advances one step at a time. If there’s a loop, eventually, the fast pointer will catch up to the slow pointer, indicating the presence of a loop.

62. What are the properties of a balanced binary tree?

Ans:

A balanced binary tree is characterized by having approximately the same number of nodes in the left and right subtrees, ensuring that the height of the tree is minimized. This characteristic makes sure that operations like searching, insertion, and deletion are done quickly and with a temporal complexity that grows with the number of elements.

63. Explain the concept of graph traversal and its applications

Ans:

• Graph traversal involves visiting all the vertices (nodes) of a graph systematically. 
• It is used to explore or search a graph, typically to find paths or to visit each vertex exactly once. 
• Depth-first search (DFS) and breadth-first search (BFS) are two popular graph traversal techniques.

64. How do you implement a priority queue using an array?

Ans:

To implement a priority queue using an array, we can use a binary heap data structure. In a binary heap, each element has a priority associated with it, and the highest priority element is always at the root. We maintain the heap property by ensuring that the parent node’s priority is higher than or equal to its children’s priorities.

65. Describe the process of converting an infix expression to a postfix expression.

Ans:

To convert an infix expression to a postfix expression, we use the shunting-yard algorithm. We iterate through each token in the infix expression and process it accordingly. We use a stack to temporarily store operators and output operands in postfix notation based on their precedence and associativity.

66. What are the advantages and disadvantages of using a hash table?

Ans:

• Advantages: Hash tables provide constant-time average-case lookup, insertion, and deletion operations. They offer efficient data retrieval and are suitable for implementing associative arrays, sets, and dictionaries.
• Disadvantages: Hash tables require a good hash function to minimize collisions. Resolving collisions can impact performance, and they may have a higher memory overhead compared to other data structures.

67. Explain the concept of dynamic programming and its relation to data structures.

Ans:

Dynamic programming is a technique for solving problems by breaking them down into smaller subproblems and solving each subproblem only once. It often involves storing the solutions to subproblems in a data structure, such as an array or a matrix, to avoid redundant computations. Dynamic programming is closely related to certain data structures, such as arrays and memoization tables.

68. What is the difference between a linked list and an array?

Ans:

An array is a sequential collection of elements stored in contiguous memory locations, allowing constant-time random access. In contrast, a linked list is a linear data structure where elements are stored in nodes, each containing a reference to the next node. Linked lists support dynamic memory allocation and efficient insertion and deletion operations, but they lack random access.

69. What is the significance of tree height in binary trees?

Ans:

• The height of a binary tree indicates the maximum number of edges from the root to a leaf node.
• It determines the overall efficiency of tree operations like insertion, deletion, and searching.
• A balanced binary tree with minimal height ensures optimal performance of these operations.
• Higher tree height can lead to increased time complexity for traversal and manipulation.

70. How can you implement a hash table using separate chaining?

Ans:

• Hash table using separate chaining resolves collisions by maintaining a linked list at each hash table index.
• Each linked list stores key-value pairs that map to the same hash code.
• When inserting or searching for an element, the hash code is calculated to determine the corresponding linked list.
• This approach ensures constant-time complexity for insertion and retrieval operations on average.
• However, it may lead to degraded performance if the hash function generates many collisions.

71. How do you implement a binary search algorithm iteratively?

Ans:

To implement binary search iteratively, we initialize two pointers, low and high, to the start and end indices of the array, respectively. We repeatedly divide the search space in half by calculating the mid index. If the target element is found at the mid index, we return its position. Otherwise, we adjust the pointers based on whether the target is greater or smaller than the mid element until the search space is exhausted.

72. Describe the process of finding the shortest path in a weighted graph.

Ans:

To find the shortest path in a weighted graph, we typically use algorithms such as Dijkstra’s algorithm or Bellman-Ford’s algorithm. Dijkstra’s algorithm is used for graphs with non-negative edge weights and finds the shortest path from a single source vertex to all other vertices. Bellman-Ford algorithm handles graphs with negative edge weights and detects negative-weight cycles, if any, in addition to finding the shortest paths.

73. Explain the concept of graph representation using an adjacency matrix and adjacency list.

Ans:

• The adjacency matrix represents a graph as a 2D array where matrix[i][j] denotes the presence of an edge between vertices i and j.
• It’s suitable for dense graphs but requires more memory, consuming O(V^2) space.
• An adjacency list represents a graph as an array of linked lists, where each list stores adjacent vertices for a specific vertex.
• It’s efficient for sparse graphs and consumes less memory, typically O(V + E) space.

74. What are the characteristics of a balanced binary search tree?

Ans:

• A balanced binary search tree maintains a relatively uniform height across its subtrees.
• It guarantees that there is little variation in height between any node’s left and right subtrees.
• Balanced trees like AVL trees and Red-Black trees enforce specific balancing criteria to achieve this balance.
• As a result, operations like insertion, deletion, and searching have optimal time complexity.

75. Describe the process of performing a breadth-first search on a graph.

Ans:

Breadth-First Search (BFS) explores a graph by visiting all its neighboring vertices at the current depth level before moving to the next level. It employs a queue data structure to maintain the order of exploration. Starting from a chosen vertex, BFS systematically traverses the graph level by level. It ensures that all vertices are visited once and that the shortest path is found from the starting vertex to any other reachable vertex. BFS is often used for tasks such as finding the shortest path, connecting components, and cycle detection in graphs.

76. How do you implement a queue using an array?

Ans:

First-in-first-out (FIFO) is a linear data structure that is adhered to by queues. Implementing a queue using an array involves maintaining two pointers, front and rear, to track the queue’s elements. The enqueue operation adds elements to the rear of the queue, while the dequeue operation removes elements from the front. Both operations have a time complexity of O(1) when implemented with an array. However, the array implementation may face issues with dynamic resizing and efficient memory utilization.

77. Explain the concept of lazy deletion in a binary search tree.

Ans:

• Lazy deletion is a technique used to mark nodes for deletion in a binary search tree without immediately removing them.
• Instead of physically deleting a node, its status is updated to indicate it has been marked for removal.
• This approach avoids restructuring the tree immediately, which can be costly in terms of time and resources.
• Deleted nodes are typically ignored during search and traversal operations but are retained in the tree structure.

78. What are the advantages of using a trie data structure for storing strings?

Ans:

• A tree is a tree-like data structure optimized for storing and searching strings.
• It offers fast lookup times, typically O(m), where m is the length of the string, making it efficient for dictionary-like applications.
• Tries to excel at prefix-based searches, making them suitable for autocomplete and spell-checking functionalities.
• They require less memory than hash tables to store large sets of strings, especially when many strings share common prefixes.

79. Describe the process of performing an inorder traversal of a binary tree.

Ans:

Inorder traversal visits nodes in a binary tree in the order (left, root, right). It systematically explores the left subtree, then visits the current node, and finally traverses the right subtree. Inorder traversal yields elements in sorted order when applied to a binary search tree. This traversal technique is commonly used for tasks like printing tree elements in ascending order. Recursive implementation of inorder traversal follows a depth-first approach, visiting nodes in a bottom-up fashion.

80. How do you implement a binary search tree deletion operation?

Ans:

Deleting a node from a binary search tree involves several cases depending on the node’s position and subtree structure. If the node to be deleted is a leaf node or has only one child, it can be removed straightforwardly. One common approach for nodes with two children is to find the in-order successor or predecessor to replace the node. After replacement, the successor/predecessor node is deleted recursively from its original position. Special care must be taken to update the tree’s structure and maintain its properties after deletion.

81. What is the difference between a binary heap and a binomial heap?

Ans:

• Every node in a binary tree that meets the heap property is called a binary heap. 
• Binomial Heap is a collection of binomial trees that satisfy the heap property.
• Binary Heap supports efficient insertion and deletion but may require heapify operations.
• Binomial Heap allows for faster merge operations and supports more efficient decrease key operations.

82. Explain the concept of backtracking and its applications in data structures.

Ans:

• Backtracking is a problem-solving strategy that involves considering every potential outcome.
• It involves systematically trying different options and backtracking from choices that do not lead to a solution.
• Applications include solving problems like the N-Queens problem, Sudoku, and graph coloring.
• Backtracking is widely used in combination with recursion to efficiently explore solution spaces.

83. What are the advantages of using a self-balancing tree over a regular binary tree?

Ans:

• Self-balancing trees automatically adjust their structure to maintain balance, ensuring predictable performance.
• They prevent degeneration into linked lists, which can occur in unbalanced binary trees, ensuring logarithmic time complexity for operations.
• Self-balancing trees, such as AVL and Red-Black trees, offer efficient insertion, deletion, and search operations with guaranteed time complexity.
• They are suitable for applications requiring dynamic data structures with balanced height.

84. Describe the process of performing a depth-first search on a graph.

Ans:

Depth-First Search (DFS) explores as far as possible along each branch before backtracking. Start with a vertex and visit its adjacent unvisited vertices recursively. Repeat the process until all reachable vertices are visited. Either a stack data structure or recursion can be used to implement DFS. It’s commonly used to find connected components, detect cycles, and traverse trees and graphs. DFS typically requires marking visited vertices to avoid infinite loops and to ensure all vertices are visited.

85. How can you implement a stack using two queues?

Ans:

Use Queue1 for push operation and Queue2 for pop operation. For push operation, enqueue the element into Queue1. Dequeue every element from Queue 1 (apart from the final one) and enqueue it into Queue 2 for the pop operation. The final element in Queue 1 should be dequeued and returned as the popped element. Swap Queue1 and Queue2 to maintain the order for subsequent operations. This approach ensures FIFO order for elements in the stack while utilizing the properties of queues.

86. What is the significance of tree balancing in AVL trees?

Ans:

• Tree balancing in AVL trees ensures that the height difference between left and right subtrees (balance factor) is at most one.
• I am balancing guarantees logarithmic time complexity for insertion, deletion, and search operations.
• AVL trees maintain balance through rotations, including single and double rotations, to restore balance after insertions or deletions.
• Balanced trees like AVL trees offer predictable performance and efficient operations even in dynamic environments.

87. Explain the concept of amortized analysis in the context of data structures.

Ans:

• Amortized analysis evaluates the average time complexity of operations over a sequence of operations.
• It accounts for both the costly and non-costly operations, distributing the cost evenly.
• Amortized analysis is useful for understanding the performance of data structures with expensive operations.
• It ensures that the overall cost of operations remains low, even if individual operations are occasionally expensive.

88. What are the properties of a red-black tree, and how are they maintained?

Ans:

Red-Black trees are binary search trees with additional properties that ensure balance. Properties include nodes being colored red or black and specific rules regarding adjacent nodes’ colors. Red-Black trees maintain balance through rotations and color changes during insertions and deletions. Properties such as red nodes having only black children and every path from the root to the leaf having the same number of black nodes are maintained. These properties ensure that the tree remains approximately balanced, guaranteeing logarithmic time complexity for operations.

89. Describe the process of performing a preorder traversal of a binary tree.

Ans:

• Preorder traversal visits the root node first, followed by the left subtree, and then the right subtree recursively.
• Start with the root node.
• Visit the root node.
• Recursively traverse the left subtree.
• Recursively traverse the right subtree.
• This traversal order is useful for generating prefix expressions, copying binary trees, and evaluating expression trees.

90. How do you implement a heap sort algorithm?

Ans:

Heap Sort is a comparison-based sorting algorithm that uses a binary heap data structure. Convert the input array into a max heap. Swap the root node (maximum element) with the last node in the heap and decrease the heap size. Restore the max heap property by clarifying the remaining elements. Repeat the process until all elements are removed from the heap. The sorted array is obtained by extracting elements from the heap in descending order.

91. What are the advantages of using a B-tree over a binary tree?

Ans:

• B-trees handle large datasets efficiently due to their balanced structure.
• They reduce disk I/O operations by storing more keys in each node.
• B-trees support efficient insertion, deletion, and search operations.
• They maintain a more stable height, leading to better performance.
• File systems and databases work well with b-trees.

92. Explain the concept of topological sorting and its applications.

Ans:

Topological sorting arranges nodes in a directed graph based on their dependencies. It is commonly used in task scheduling, such as in project management. Topological sorting helps identify dependencies and order tasks accordingly. Applications include scheduling jobs with dependencies and resolving dependencies in build systems. It ensures that no task is executed before its prerequisites are completed. Topological sorting is essential in optimizing task execution order.

93. How can you implement a priority queue using a linked list?

Ans:

Each node in the linked list contains an element and its priority. Insertion involves finding the correct position based on priority. Removal retrieves the element with the highest priority. Linked lists support dynamic size, allowing for efficient insertion and removal. Priority queues can be implemented as a single or doubly linked list. Linked list-based priority queues are suitable for applications with frequent priority changes.

94. What are the characteristics of a binary search tree with duplicate keys?

Ans:

• Allows duplicate keys, which can be stored in either the left or right subtree.
• Insertion of duplicate keys can be handled differently based on the implementation.
• Searching for a duplicate key returns the first occurrence found during traversal.
• Deletion may require careful handling to maintain the tree’s binary search property.

95. Describe the process of performing a depth-limited search on a graph.

Ans:

• Depth-limited search is a variant of depth-first search with a depth limit.
• It explores each branch of the graph up to a specified depth limit.
• If a node’s depth exceeds the limit, it is not expanded further.
• Depth-limited search is useful for iterative deepening depth-first search.
• Applications include solving puzzles, game playing, and AI search algorithms.

96. What is the significance of tree rotation in AVL trees?

Ans:

Tree rotation maintains the balance factor of nodes in AVL trees. It helps in restoring the AVL tree’s height balance after insertions or deletions. There are two types of rotations: left and right. Double rotations, such as left-right and right-left rotations, are used to rebalance subtrees. Tree rotation ensures that the tree remains balanced, optimizing search operations. Properly balanced AVL trees provide efficient insertion, deletion, and search operations.