
- What is Hill Cipher?
- How Does the Hill Cipher Work?
- Key Features of the Hill Cipher
- Modern Applications of the Hill Cipher
- Advantages and Limitations of the Hill Cipher
- Cryptographic Techniques: The Evolution Beyond Hill Cipher
- Security of the Hill Cipher
- Conclusion
Hill Cipher is one of the most significant classical encryption techniques widely used in cryptography. It was discovered in 1929 by a mathematician named Lester S. Hill. This is one of the great inventions that marks a significant improvement in cryptogram methods, which now use linear algebra to encrypt and decrypt messages. hill cipher cryptography works through block Encrypts to generate decryption and encryption functions for blocks of letters by working under matrix multiplication. In contrast, unlike most other simple cyphers, including the Caesar Cipher, which merely exchanges letters with a set, fixed sequence, the Hill Cipher works to execute end to end encryption as well as decryption of hill cipher on the blocks of letters. The power built for Cybersecurity Training Course is built in mathematical principles.This lengthy tutorial covers the basics of Hill Cipher, its applications, advantages, limitations, and the underlying mathematical concepts. Thus, it would make sense to beginners in cryptography, and advanced learners would deepen their understanding of the key elements of the Hill Cipher.
What is Hill Cipher?
The Hill Cipher is a polygraphic substitution cypher at its heart. In addition to replacing the traditional system whereby each letter of the alphabet is replaced by another letter independently, it maps groups of letters into others that are usually pairs or triplets and substitutes through matrix operations. One of the first cyphers to use linear algebra for encrypting was much more complex and secure than the previous cyphers. It uses a key matrix as a square matrix of n × n size, n being the number of letters in a block, to cypher the plaintext into ciphertext. The transformation of letters according to the matrix makes this cypher fit neatly into matrix-based cryptography through Keylogger modular arithmetic.The matrix transformation of the letters brings this end to end encryption right into the fold of matrix-based cryptography using modular arithmetic.
Sign up for ACTE Cyber Security Online Training and get a head start in your career cyber security.
How Does the Hill Cipher Work?
The process of how the Hill Cipher works can be followed by determining the encryption and decryption of hill cipher of a message. Essentially, the Hill Cipher involves matrix multiplication and modular arithmetic. The steps on how the Hill Cipher works are as follows:
- The key matrix will be invertible That is, the determinant of the key matrix must be coprime with the modulus (usually 26 to represent the 26 letters of the English alphabet). Here’s an example of a typical key matrix for a 2×2 cypher:
- Convert Plaintext into Numeric FormReplace every plaintext letter with a number according to their positions within the alphabet.Suppose A = 0, B = 1, C = 2,…, Z = 25.If the block size is 2, for example, a 2×2 matrix, then the plaintext will be grouped into pairs of letters.Example: The word “HELLO” is encoded as the pairs (H, E), (L, L), and (O, X) (adding “X” to make the final pair).
- Matrix MultiplicationThe plaintext will be represented as a column vector and multiplied by the key matrix to encode a pair of letters. For example, when the first pair is “HE” (H = 7, E = 4), the equation will be:
- Decrypting the Ciphertext
To read the message, the recipient needs the key matrix and its inverse. decryption of hill cipher is just the reverse of end to end encryption to decrypt the ciphertext, multiply it by the inverse of the key matrix modulo 26.
If the key matrix is:

Then the inverse of K, denoted K^−1, can be computed as
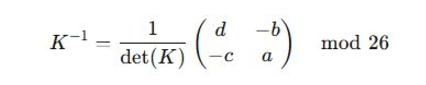
Once the inverse matrix is obtained, it is multiplied by the crypto text vector, and the result is the original plaintext vector.
Key Features of the Hill Cipher
- Polygraphic Cipher:Hill Cipher is other than a substitution cypher because it involves more than one letter at a time for Encrypts. Accordingly, the effect of frequency analysis is also reduced.
- Matrix-Based Encryption:Thehill cipher cryptography is based on matrix multiplication, and the complexity is slightly greater.
- Key Size Flexibility:It allows changing any block size with a larger matrix key. The more gigantic the matrix, the more the Web Security will be, thus the more it is computational.
- Simple to Implement:It is straightforward to implement. Although the mathematics behind the Hill Cipher is very complex, it is simple to implement as an application of the Hill Cipher can be carried out through a simple matrix multiplication and forms a good teaching tool on the basic concepts of cryptography and linear algebra.
- Resistance to Frequency Analysis:The Hill Cipher is much more secure than classical substitution cyphers because it encrypts multiple letters simultaneously, making it harder for attackers to use frequency analysis to break the code.
- Simple Concept: The mathematical foundation of the Hill Cipher, based on matrix operations and modular arithmetic, is easy to understand, especially for those with a background in linear algebra.
- Encryption Strength: Hill Cipher can provide relatively strong encryption with other Cybersecurity Training Courses, using bigger matrices such as 3×3 or 4×4.
- Key Management:In the Hill Cipher, the two parties involved in communication, the sender and receiver, must share the same.Thus, a secure way of exchanging large keys is required, which may become cumbersome to handle securely with an increasing matrix size.
- Known-Plaintext Attacks: Any attacker who knows a part of the plaintext with the corresponding ciphertext can infer the key matrix, thus compromising Hill Cipher, which is unsecured in contrast to more recent algorithms like AES.
- Complexity in Larger Matrices: The bigger the matrices, the more complicated the end to end encryption. Both processes involve more computations: the process to calculate the inverse of the matrix modulo 26 is required to decrypt it in the bigger matrix.
- Known plaintext attack:If the attacker has both plaintext and corresponding ciphertext, they may be able to retrieve the key matrix by applying linear algebra techniques.
- Chosen-plaintext Attack:The attacker can select some known text blocks and deduce the key matrix from the corresponding ciphertext.
Are you curious to know more about Cybersecurity ? Take advantage of our comprehensive online Cyber Security Online Training .
Modern Applications of the Hill Cipher
Though the Hill Cipher is something of the past and has lost its place to stronger variants like RSA and AES, it still finds application in education and historical cryptography. The hill cipher cryptography remains an important topic within any cryptography course taught in the context of matrix operations, modular arithmetic, or linear algebra. It is one of the direct examples of polygraphic substitution, whereby multiple letters at once are encrypted using matrix multiplication, further deepening understanding of block cyphers, which find application in modern algorithms like AES. It also helps provide a useful tool for the Hill cypher for cryptographic research as an applicable tool. Though prone to known plaintext attacks, it allows students and researchers to test various cryptographic attacks and acquire basic knowledge of Database Security principles.
The Hill Cipher is generally researched in history for its applications in early 20th-century use, particularly within military cryptography and cipher reconstruction projects. It has always remained of interest among cryptographic historians and enthusiasts regarding how these people have used encryption throughout the ages. This forms the foundation of the construction of modern block cyphers within cryptography. Even if old for secure communication, it remains a foundational tool of the discipline, which could equip anyone with the mathematical side of cryptography and information regarding the evolution of ways Encrypts methods have followed.
Advantages and Limitations of the Hill Cipher
Advantages
Limitations
Want to Take the Lead in Cyber Security ? Enroll in ACTE’s Cybersecurity Expert Masters Program Training Course Program to Begin Your Adventure Now.
Cryptographic Techniques: The Evolution Beyond Hill Cipher
Though Hill Cipher was a breakthrough for its time of invention, the first example of the use of linear algebra in the later cryptographic developed was superior to Hill regarding Security and efficiency. Due to its symmetric nature, the hill cipher cryptography was primarily vulnerable to known plaintext attacks, and brute force limited its use for any practical application where sensitive information must be protected. More powerful, secure algorithms and algorithms require the passage of time since the development of technology is unstoppable. This leads to the idea of advanced algorithms in general.The second-generation changeover is the so-called Hill Cipher and the well-known RSA and ECC. The other technique, known as symmetric encryption, differs from this and asymmetric cryptography due to using just one key for encryption and decrypting purposes in the former. At the same time, two keys are used for encryption and decrypting purposes in the latter, commonly referred to as public and private keys.
Hill Cipher, though, is still helpful in a course in cryptography. This eliminates a need for the safe diffusion of keys among participants; it accommodates digital signature schemes and Resolution Protocol for exchanging keys and safe and online transactions over the Net. RSA works on the principle that it is hard to factor a composite number into its prime factors. In contrast, ECC works on elliptic curve mathematics and provides strong encryption through much smaller key sizes, providing greater efficiency for new applications. Another is symmetric encryption, such as AES, which replaces the Hill Cipher in terms of safety and performance. AES encrypts secret information everywhere. Its algorithms are much more complex, and the keys are much longer, so its encryption is stronger. The hill cipher cryptography provides a basis for understanding matrix-based encryption and modular arithmetic and for learning about the fundamental principles on which modern block cyphers and other techniques are based. It shows how the methods developed from the simple concepts in the earlier systems to the complex systems used today.
Security of the Hill Cipher
The Hill Cipher is more secure than the simple Caesar or monoalphabetic substitution cyphers. But it’s not an exception to cryptanalysis. Some of its weaknesses are as below.
Despite these shortcomings, the Hill Cipher is the precursor of some modern encryption algorithms and was commonplace in early cryptography. However, with the advent of comparatively complex algorithms such as RSA and AES, the Hill Cipher is rarely used today in practice except perhaps in tutorial environments or simple basic Web Application Security .
Preparing for a job Interview? Check out our blog on Cybersecurity Interview Questions and Answers !
Cryptographic Techniques Sample Resumes! Download & Edit, Get Noticed by Top Employers! DownloadConclusion
The Hill Cipher was an important technique in the history of encryption. It introduces a more advanced version of a substitution cypher involving matrix multiplication and linear algebra. However, it has yet to be used practically. Modern cryptography methods have overtaken it. However, this tool should be included in terms of the mathematical roots of encryption included. As the most trivial of Hill Ciphers, it clearly shows what beauty can be applied to secure communications through simple Cybersecurity Training while, at the same time, maintaining relevance in contemporary applications.
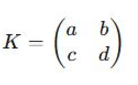
The values of the elements of the matrix a, b, c, and d are randomly chosen such that the determinant of the matrix is not equal to zero and is also not a multiple of 26.

Now, multiply the key matrix K with the plaintext vector P: C=K×Pmod26 The two numbers that multiply to this value have their corresponding letter values added to create the new vector C, which is the ciphertext. The values are mapped back to letters (e.g., 3 = D, 15 = P, etc.). This process repeats for every pair or block of letters in the plaintext.





