What Is Recursion in Python? Explained with Simple Examples

What is Recursion?

Recursion is a programming technique in which a function calls itself to solve smaller instances of the same problem. In Python, recursion is a powerful tool that allows programmers to write elegant and concise code for tasks that have a naturally recursive structure, such as tree traversal, combinatorics, and mathematical sequences. The recursive function continues to call itself with modified arguments until a base case is met, which ends the chain of calls and allows the results to propagate back through the previous calls. Recursion is a programming concept where a function calls itself to solve a smaller instance of the same problem. This technique is widely used in computer science to simplify complex problems by breaking them down into more manageable sub-problems. A recursive function typically includes two key components: a base case, which stops the recursion, and a recursive case, where the function continues to call itself with modified input. Without a base case, recursion can lead to infinite loops and eventually a stack overflow error. Common examples of problems suited for recursion include calculating factorials, generating Fibonacci sequences, traversing trees, and solving puzzles like the Tower of Hanoi. While recursion can make code more elegant and easier to understand in some cases, it may also lead to performance issues due to the overhead of multiple function calls and memory usage. Therefore, it’s important to understand when and how to use recursion effectively. Many modern programming languages, including Python, support recursion, Components of a Recursive, though each has its own limitations on recursion depth. Ultimately, recursion is a powerful tool in a programmer’s toolkit, especially when working with problems that exhibit repetitive, nested, or self-similar patterns.

To Earn Your Web Developer Certification, Gain Insights From Leading Data Science Experts And Advance Your Career With ACTE’s Web Developer Courses Today!

Components of a Recursive Function

A recursive function has two main components: the base case and the recursive case. The base case is a condition under which the function returns a value without making a recursive call. It acts as the stopping criterion to prevent infinite recursion. The recursive case defines how the function calls itself with a modified input to approach the base case.

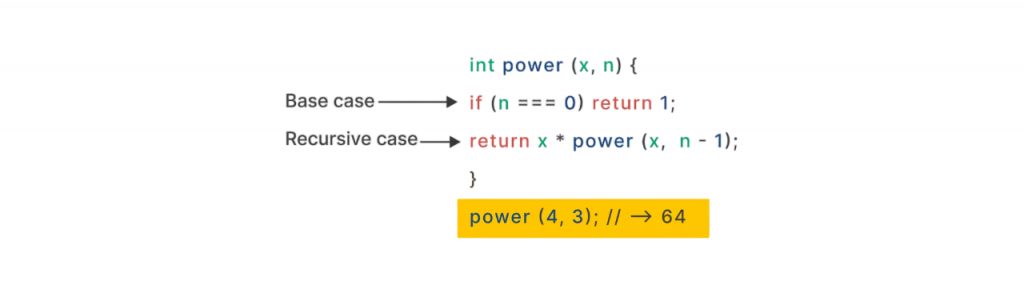
For example, in a function to calculate factorial:

• def factorial(n):
• if n == 0:
• return 1
• else:
• return n * factorial(n – 1)

Here, n == 0 is the base case, and n * factorial(n – 1) is the recursive case.

Subscribe To Contact Course Advisor

Subscribe

Base Case and Recursive Case

The base case is crucial to ensure that recursion terminates. Without a base case, the recursive function would keep calling itself indefinitely, eventually leading to a stack overflow error. The recursive case defines the progression toward the base case. Let’s consider the Fibonacci sequence:

• def fibonacci(n):
• if n == 0:
• return 0
• elif n == 1:
• return 1
• else:
• return fibonacci(n-1) + fibonacci(n-2)

In this function, n == 0 and n == 1 are the base cases, while the recursive case breaks the problem into smaller subproblems by calling fibonacci(n-1) and fibonacci(n-2).

Would You Like to Know More About Web Developer? Sign Up For Our Web Developer Courses Now!

Examples (Factorial, Fibonacci)

Factorial Example:

• def factorial(n):
• if n == 0:
• return 1
• else:
• return n * factorial(n – 1)

Calling factorial(5) returns 5 * 4 * 3 * 2 * 1 = 120.

Fibonacci Example:

• def fibonacci(n):
• if n <= 0:
• return 0
• elif n == 1:
• return 1
• else:
• return fibonacci(n – 1) + fibonacci(n – 2)

Calling fibonacci(6) returns 8, as the sixth Fibonacci number is 8. These examples show how recursion breaks problems down into smaller, manageable subproblems.

Develop Your Skills with Web Developer Certification Course

Weekday / Weekend BatchesSee Batch Details

Stack Behavior in Recursion

Each recursive call is placed on the call stack. The stack records the function and its local variables until it reaches the base case. Then the calls are resolved in reverse order (Last In, First Out). This stack-based nature can lead to a stack overflow if the recursion depth is too great. When a function calls itself recursively, each call is placed on the call stack, a special data structure that tracks function calls in most programming languages. This stack follows a Last In, First Out (LIFO) behavior; the most recent function call is the first to be completed and removed from the stack.

For example, in factorial(5), the call stack will build up with factorial(5), factorial(4), and so on, until factorial(0) is reached. Then, the results are returned back up the stack. This behavior is inherent to how functions are executed and returned in memory.

Are You Interested in Learning More About Web Developer? Sign Up For Our Web Developer Courses Today!

Tail Recursion Concepts

Tail recursion is a specific form of recursion where the recursive call is the last operation in the function. Some programming languages optimize tail recursion to prevent stack overflow. Unfortunately, Python does not perform tail call optimization, which means deep tail-recursive functions will still hit the recursion limit. Tail recursion is a special type of recursion where the recursive call is the last operation performed by the function before it returns a result. In other words, there is no further computation needed after the recursive call. This structure allows certain programming languages or compilers to optimize the recursion by reusing the current function’s stack frame, a technique known as tail call optimization (TCO). As a result, tail-recursive functions can execute in constant stack space, just like iterative loops, which makes them more memory-efficient.

Example of tail recursion:

• def tail_factorial(n, acc=1):
• if n == 0:
• return acc
• else:
• return tail_factorial(n-1, n*acc)

While this is tail-recursive in nature, Python will not optimize it differently than a regular recursive function.

Recursion vs Iteration

Recursion and iteration are both techniques to perform repetitive tasks. Recursion uses function calls, while iteration uses loops. Recursion is often more readable and elegant for problems like tree traversal or factorial, but it can be inefficient in terms of memory and execution time.

For example, a factorial function using iteration:

• def iterative_factorial(n):
• result = 1
• for i in range(1, n + 1):
• result *= i
• return result

This version uses constant space and is generally more efficient than its recursive counterpart.

Maximum Recursion Depth in Python

In Python, there is a limit to how deeply functions can recurse, known as the maximum recursion depth. This limit exists to prevent infinite recursion from consuming all available stack memory, which would crash the program. By default, Python’s maximum recursion depth is set to 1000, though this can vary slightly depending on the Python version and platform.

import sys

print(sys.getrecursionlimit())

sys.setrecursionlimit(2000)

Attempting to exceed the recursion limit will raise a RecursionError. It’s important to design recursive functions with appropriate base cases and to avoid unnecessary depth.

Web Development Sample Resumes! Download & Edit, Get Noticed by Top Employers! Download

Conclusion

Recursion is a powerful concept in Python that simplifies problem-solving by breaking down tasks into smaller subproblems. It involves function self-calls with a clear base case and recursive case. While elegant and intuitive for many algorithms, Components of a Recursive must be used with care due to potential stack overflow and performance limitations. Understanding its principles, use cases, and limitations allows developers to choose when to use recursion effectively and when to rely on more efficient alternatives like iteration or memoization. Recursion is a powerful programming technique that allows a function to solve complex problems by calling itself on smaller subproblems. Understanding how recursion works including stack behavior, tail recursion, and Python’s recursion limits is essential for writing efficient and safe recursive functions. While recursion can make code cleaner and more elegant, it must be used with care to avoid exceeding Python’s default recursion depth, which can lead to a RecursionError. In cases where recursion gets too deep, converting the logic to an iterative solution may be a better choice. Mastering recursion equips you to tackle a wide range of algorithmic challenges effectively.