
- What is Backtracking?
- Key Concepts: State Space, Constraints
- General Template of Backtracking
- N-Queens Problem
- Rat in a Maze
- Sudoku Solver
- Subset and Permutation Generation
- Binary Decision Trees
- Time Complexity of Backtracking
- Code Samples in C++/Python
- Optimization Tips
- Conclusion
What is Backtracking?
Backtracking is a powerful algorithmic technique used to solve recursive problems that involve exploring all possibilities in a smart, efficient way. Instead of blindly checking every path (like brute force), backtracking prunes the search space by abandoning paths that are clearly invalid. To complement such algorithmic strategies with front-end development skills, Web Developer Training can help developers build interfaces that visually guide users through logical flows and decision paths. It is especially useful in constraint satisfaction problems like puzzles, permutations, and path-finding. Backtracking is a method for building up to a solution incrementally, one piece at a time, and removing those solutions that fail to satisfy the problem constraints as soon as they are detected.
To Earn Your Web Developer Certification, Gain Insights From Leading Web Developer Experts And Advance Your Career With ACTE’s Web Developer Courses Today!
Key Concepts: State Space, Constraints
To understand backtracking, you need to understand how environments support iterative development and debugging. Exploring What is PyCharm can help clarify how this powerful IDE streamlines Python coding, making it easier to implement and test recursive algorithms like backtracking.
State Space Tree:
- A tree structure where each node represents a partial solution.
- Leaves may represent complete solutions.
- The algorithm explores branches, and if a branch violates constraints, it backtracks to try another path.
Constraints:
- Rules that restrict the choices.
- Examples:
- No two queens in the same row/column (N-Queens)
- A digit appears only once in a row/column/box (Sudoku)
Feasibility Function:
- A check to see if the current state satisfies constraints before proceeding.
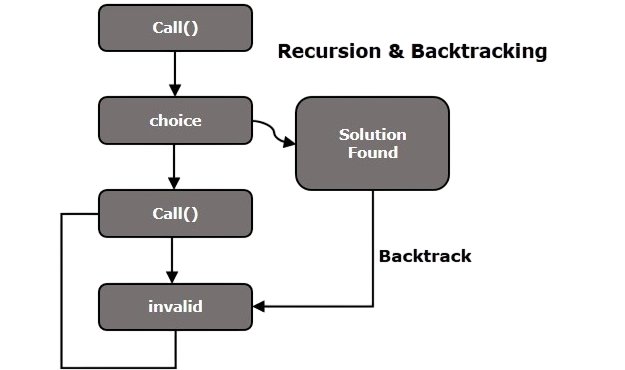
General Template of Backtracking
General Template of Backtracking involves recursive exploration and conditional pruning to efficiently navigate solution spaces. To understand how asynchronous systems handle such logic at scale, exploring Node JS Architecture reveals how event-driven models and non-blocking I/O support high-performance execution in real-world applications.
- def backtrack(path, options):
- if goal_reached(path):
- output.append(path[:])
- return
- for option in options:
- if is_valid(option, path):
- path.append(option)
- backtrack(path, options)
- path.pop() # backtrack
This approach applies to permutations, subsets, game solving, etc.
N-Queens Problem
The classic N-Queens problem asks: Place N queens on an N×N chessboard such that no two queens attack each other. To strengthen your problem-solving foundation and explore career-ready skills, enrolling in Technical Courses After Graduation can help you apply algorithmic thinking to real-world domains like software development, data science, and system design.
Backtracking Logic for N-Queens Problem:
Python Snippet:
- def solve_n_queens(n):
- board = []
- def is_safe(r, c):
- for i in range(r):
- if board[i] == c or abs(board[i] – c) == r – i:
- return False
- return True
- def backtrack(r):
- if r == n:
- result.append(board[:])
- return
- for c in range(n):
- if is_safe(r, c):
- board.append(c)
- backtrack(r + 1)
- board.pop()
- result = []
- backtrack(0)
- return result
- # Time complexity: O(N!)
- Place queens one row at a time.
- For each row, try all columns.
- Check column and diagonal safety.
- If safe, place the queen and move to the next row.
- If a dead-end is hit, backtrack.
- Move only in allowed directions (e.g., right and down).
- Can’t visit blocked or already visited cells.
- Check if the current move is valid.
- If at destination, store path.
- Try all possible directions.
- Backtrack when stuck.
- def rat_in_maze(maze, x, y, path, visited):
- if x == len(maze)-1 and y == len(maze[0])-1:
- print(path)
- return
- dirs = [(0,1,’R’), (1,0,’D’), (0,-1,’L’), (-1,0,’U’)]
- for dx, dy, move in dirs:
- nx, ny = x+dx, y+dy
- if 0 <= nx < len(maze) and 0 <= ny < len(maze[0]) and maze[nx][ny] == 1 and not visited[nx][ny]:
- visited[nx][ny] = True
- rat_in_maze(maze, nx, ny, path+move, visited)
- visited[nx][ny] = False
- Fill a 9×9 grid so each row, column, and 3×3 box has digits 1–9.
- Find an empty cell.
- Try placing 1 to 9.
- If valid, recurse; else, try the next number.
- Backtrack when no valid number fits.
- def is_valid(board, row, col, num):
- for i in range(9):
- if board[i][col] == num or board[row][i] == num or \
- board[3*(row//3)+i//3][3*(col//3)+i%3] == num:
- return False
- return True
- def solve(board):
- for i in range(9):
- for j in range(9):
- if board[i][j] == ‘.’:
- for num in ‘123456789’:
- if is_valid(board, i, j, num):
- board[i][j] = num
- if solve(board):
- return True
- board[i][j] = ‘.’
- return False
- return True
- def subsets(nums):
- res = []
- def backtrack(start, path):
- res.append(path[:])
- for i in range(start, len(nums)):
- path.append(nums[i])
- backtrack(i+1, path)
- path.pop()
- backtrack(0, [])
- return res
- def permute(nums):
- res = []
- def backtrack(path, used):
- if len(path) == len(nums):
- res.append(path[:])
- return
- for i in range(len(nums)):
- if not used[i]:
- used[i] = True
- path.append(nums[i])
- backtrack(path, used)
- path.pop()
- used[i] = False
- backtrack([], [False]*len(nums))
- return res
- Node = current subset
- Left child = exclude current element
- Right child = include current element
- void solve(int row, vector<string>& board, vector<vector<string>>& solutions, int n) {
- if (row == n) {
- solutions.push_back(board);
- return;
- }
- for (int col = 0; col < n; ++col) {
- bool safe = true;
- for (int i = 0; i < row; ++i) {
- if (board[i][col] == ‘Q’ ||
- (col – row + i >= 0 && board[i][col – row + i] == ‘Q’) ||
- (col + row – i < n && board[i][col + row – i] == ‘Q’)) {
- safe = false;
- break;
- }
- }
- if (safe) {
- board[row][col] = ‘Q’;
- solve(row + 1, board, solutions, n);
- board[row][col] = ‘.’;
- }
- }
- }
- def generate_subsets(nums):
- result = []
- def backtrack(index, path):
- result.append(path[:])
- for i in range(index, len(nums)):
- path.append(nums[i])
- backtrack(i+1, path)
- path.pop()
- backtrack(0, [])
- return result
- Constraint Pruning: Early rejection of infeasible paths saves time.
- Use Hash Sets: Useful for checking duplicates or enabling fast lookups (e.g., permutations with duplicates).
- Sort Input First: Helps in skipping duplicates and improving predictability.
- Bitmasking: Optimizes space when working with subsets and permutations.
- Memoization: Caches results for repeated subproblems, often used in variations of backtracking combined with dynamic programming.
- Heuristics: In problems like Sudoku, filling the most constrained cells first improves performance.
Would You Like to Know More About Web Developer? Sign Up For Our Web Developer Courses Now!
Rat in a Maze
Given a Rat in a Maze with obstacles, find all paths from the start to the destination.
Constraints:
Recursive Approach:
Python Snippet:
Sudoku Solver
Sudoku solving is one of the most practical uses of backtracking. While such algorithmic techniques sharpen problem-solving skills, pairing them with Web Developer Training enables developers to present logic-driven solutions through clean, interactive user interfaces.
Problem:
Python Snippet:
Are You Interested in Learning More About Web Developer? Sign Up For Our Web Developer Courses Today!
Subset and Permutation Generation
Backtracking can be used to generate all subsets, permutations, and combinations. To see how algorithmic thinking translates into real-world success, exploring App Developers Who Became Millionaires offers inspiring examples of how technical mastery and creative problem-solving can lead to breakthrough innovations and financial success.
Permutations:
Binary Decision Trees
Backtracking forms a binary decision tree in problems with 2 choices (e.g., include/exclude). To manage such branching efficiently in C++, understanding the Introduction to C++ Vectors is essential, as vectors provide dynamic storage and flexible access patterns ideal for recursive exploration.
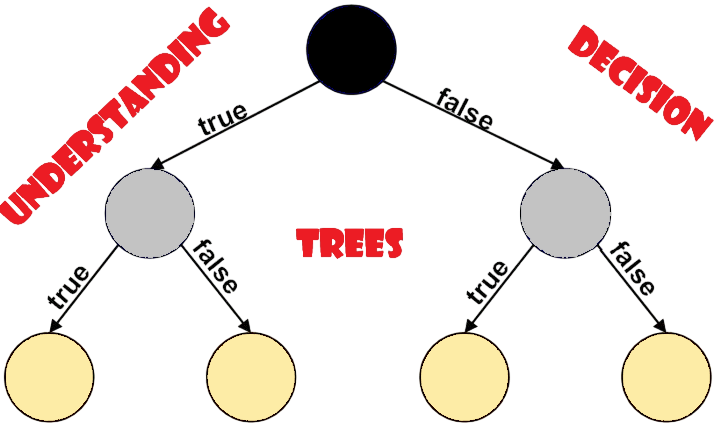
Example – Subset Sum:
This representation helps visualize how the algorithm explores paths.
Time Complexity of Backtracking
Understanding time complexity is important for analyzing algorithms, especially those that deal with decision-making. Three main factors affect time complexity: the number of decision points, the number of branches at each point, and how well pruning is done. For example, in the N-Queens problem, the complexity is O(N!), which means the time increases factorially with the number of queens. Just as optimization is key in algorithms, reviewing Tips to Avoid Application Rejection can help streamline your job search strategy by eliminating common mistakes and improving your chances of success. Permutations have a complexity of O(N × N!), while the worst-case scenario for Sudoku can reach O(9^(empty cells)), showing a major increase based on the number of empty cells.
Code Samples in C++/Python
C++ (N-Queens):
Python (Subset):
Optimization Tips
Conclusion
Backtracking is a core algorithmic paradigm used in solving complex problems where multiple choices must be tried, and constraints must be satisfied. Its recursive depth-first nature makes it intuitive to implement, while its ability to prune invalid paths makes it much more efficient than brute force. To complement such algorithmic efficiency with strong interface design skills, Web Developer Training can help developers build visually structured applications that guide users through complex logic with clarity and ease. Whether you’re solving puzzles like Sudoku, generating permutations, or traversing mazes, mastering backtracking equips you with a powerful problem-solving skill for interviews, contests, and real-world logic-based systems.





