Last updated on 13th Sep 2025| 10615
(5.0) | 32961 Ratings
E-mail this post
- Introduction to Minimum Spanning Trees (MST)
- Overview of Prim’s Algorithm
- Comparison with Kruskal’s Algorithm
- Graph Representation (Adjacency Matrix & List)
- Step-by-Step Execution of Prim’s Algorithm
- Priority Queue and Min-Heap in Prim’s Algorithm
- Pseudocode and Flowchart of Prim’s Algorithm
- Prim’s Algorithm Implementation (Python/C++/Java)
- Real-world Applications of Prim’s Algorithm
- Limitations and Edge Cases
- Summary
Introduction to Minimum Spanning Trees (MST)
In graph theory, a Minimum Spanning Tree (MST) is a subset of the edges in a connected, undirected, weighted graph that connects all the vertices together without forming any cycles and with the minimum possible total edge weight. In simpler terms, it’s a way to connect all points in a network (like cities, computers, or power stations) with the least total cost. MSTs have profound applications in network design, such as laying out electrical wiring or optimizing road construction costs. To complement such graph-based optimization with practical development skills, exploring Web Developer Training equips learners with hands-on experience in HTML, CSS, JavaScript, and full-stack frameworks empowering them to build scalable web applications that integrate algorithmic logic with real-world infrastructure planning.
To Earn Your Web Developer Certification, Gain Insights From Leading Data Science Experts And Advance Your Career With ACTE’s Web Developer Courses Today!
Overview of Prim’s Algorithm
Prim’s Algorithm is a greedy algorithm used to find the minimum spanning tree for a weighted undirected graph. The algorithm builds the MST one vertex at a time, starting from an arbitrary vertex and continuously adding the cheapest edge that connects a vertex in the MST to a vertex outside it. The core idea is to always choose the minimum weight edge that expands the tree without forming a cycle. As the algorithm proceeds, it ensures that each new addition keeps the partial tree connected and grows toward a complete MST.
Comparison with Kruskal’s Algorithm
While both Prim’s and Kruskal’s algorithms are greedy techniques for finding MSTs, their approaches differ significantly. Kruskal’s algorithm sorts all the edges and adds the smallest edge that doesn’t form a cycle, focusing on the edge-level. In contrast, Prim’s algorithm works from the vertex-level, always expanding the current MST by adding the lowest-cost edge from the known part of the graph to the unknown. Kruskal’s is better suited for sparse graphs, as it operates on edge sets, whereas Prim’s, especially with a min-heap, performs better on dense graphs where the adjacency list or matrix helps with fast lookups.
Would You Like to Know More About Web Developer? Sign Up For Our Web Developer Courses Now!
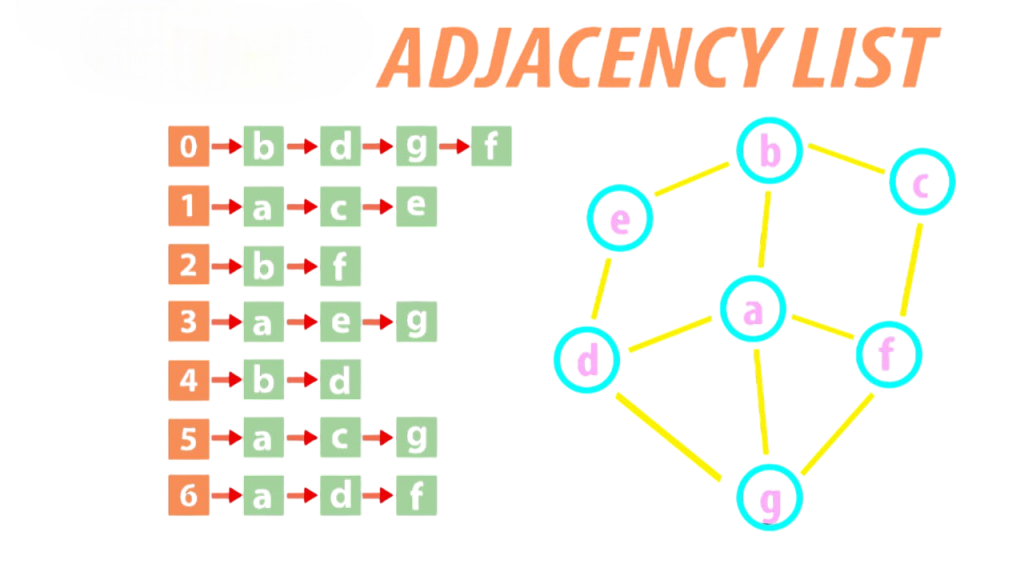
Graph Representation (Adjacency Matrix & List)
- Graphs used in Prim’s Algorithm can be represented using adjacency matrices or adjacency lists. An adjacency matrix is a 2D array where each cell (i, j) contains the weight of the edge between vertices i and j. If no edge exists, the value is often set to infinity or zero. This method provides quick access to edge weights but consumes more space, especially for sparse graphs.
- In contrast, an adjacency list represents the graph as a list of lists or a dictionary, where each vertex points to a list of connected vertices and the corresponding edge weights. This structure is memory-efficient and ideal for sparse graphs. In practice, adjacency lists are preferred in Prim’s implementation due to better scalability with larger graphs.
Develop Your Skills with Web Developer Certification Course
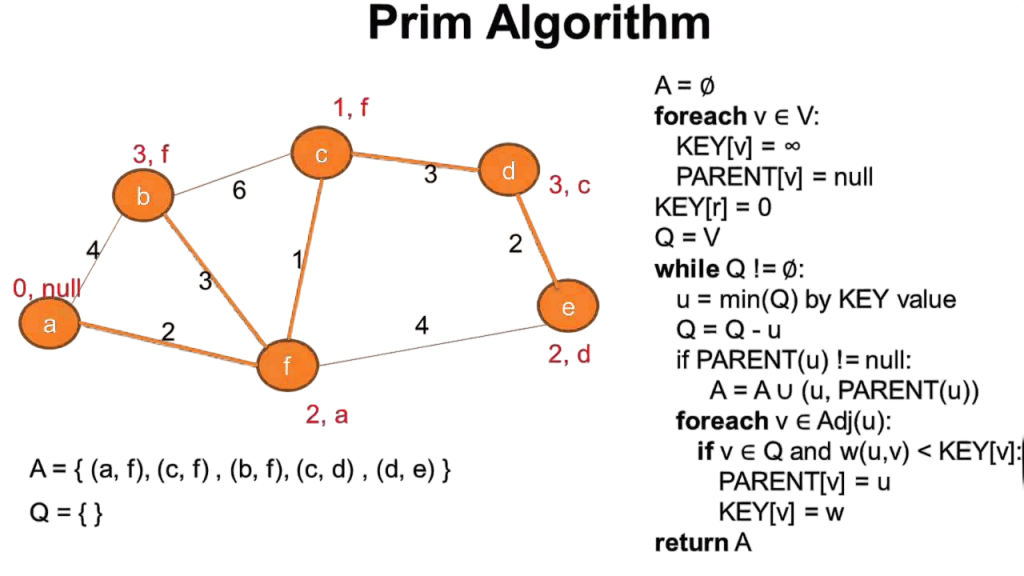
Weekday / Weekend BatchesSee Batch DetailsStep-by-Step Execution of Prim’s Algorithm
- Prim’s Algorithm starts with an arbitrary vertex, marking it as visited. From this starting point, it examines all edges that connect the visited set to unvisited vertices. It picks the edge with the lowest weight and adds it to the MST, bringing the connected vertex into the visited set. This process continues until all vertices have been included in the MST.
- Let’s consider a simple example with 5 nodes. Suppose we begin from node 0. The algorithm will scan all the edges from node 0 to its neighbors, select the smallest weight edge, say (0, 1), then from nodes {0, 1}, it will look for the next minimum edge leading to an unvisited node, and so on. This continues until all nodes are included. Throughout the process, care is taken to avoid cycles and only connect the tree to new vertices.
Are You Interested in Learning More About Web Developer? Sign Up For Our Web Developer Courses Today!
Priority Queue and Min-Heap in Prim’s Algorithm
To efficiently select the minimum weight edge at each step, a priority queue (typically implemented as a min-heap) is used. The min-heap allows the algorithm to quickly retrieve the edge with the smallest weight among all candidate edges. Each node not yet in the MST is assigned a key value that represents the minimum weight edge connecting it to the MST. To complement such graph-based optimization logic with practical development expertise, exploring Web Developer Training equips learners with hands-on experience in HTML, CSS, JavaScript, and full-stack frameworks empowering them to build scalable web applications that integrate algorithmic efficiency with real-world performance and design principles. Initially, all keys are set to infinity except the starting node, which is set to 0. As the algorithm progresses, the heap helps in efficiently updating the key values and maintaining the smallest edge at the top of the heap.
Pseudocode and Flowchart of Prim’s Algorithm
Pseudocode for Prim’s Algorithm:
- function PrimMST(graph):
- Initialize key[] = ∞ for all vertices
- key[0] = 0
- mstSet[] = False for all vertices
- parent[] = -1 for all vertices
- for each vertex in graph:
- u = vertex with minimum key[] not in mstSet
- mstSet[u] = True
- for each neighbor v of u:
- if weight(u,v) < key[v] and v not in mstSet:
- key[v] = weight(u,v)
- parent[v] = u
A flowchart of Prim’s Algorithm would show initialization, repeated selection of the minimum-weight edge, update of keys and parents, and termination when all vertices are included. It highlights the greedy nature of always selecting the best local option.
Prim’s Algorithm Implementation (Python/C++/Java)
Python Example:
- import heapq
- def prim(graph, V):
- visited = [False] * V
- min_heap = [(0, 0)] # (weight, vertex)
- total_cost = 0
- while min_heap:
- weight, u = heapq.heappop(min_heap)
- if visited[u]:
- continue
- visited[u] = True
- total_cost += weight
- for v, w in graph[u]:
- if not visited[v]:
- heapq.heappush(min_heap, (w, v))
- return total_cost
C++ Example:
- #include <iostream>
- #include <vector>
- #include <queue>
- using namespace std;
- int prim(int V, vector<pair<int, int>> adj[]) {
- vector<bool> visited(V, false);
- priority_queue<pair<int, int>, vector<pair<int, int>>, greater<>> pq;
- pq.push({0, 0});
- int totalCost = 0;
- while (!pq.empty()) {
- auto [wt, u] = pq.top();
- pq.pop();
- if (visited[u]) continue;
- visited[u] = true;
- totalCost += wt;
- for (auto [v, w] : adj[u]) {
- if (!visited[v]) {
- pq.push({w, v});
- }
- }
- }
- return totalCost;
- }
Java Example:
- import java.util.*;
- class Edge {
- int node, weight;
- Edge(int n, int w) { node = n; weight = w; }
- }
- public class Prim {
- public static int prim(List<List<Edge>> graph, int V) {
- boolean[] visited = new boolean[V];
- PriorityQueue<Edge> pq = new PriorityQueue<>(Comparator.comparingInt(e -> e.weight));
- pq.add(new Edge(0, 0));
- int total = 0;
- while (!pq.isEmpty()) {
- Edge edge = pq.poll();
- if (visited[edge.node]) continue;
- visited[edge.node] = true;
- total += edge.weight;
- for (Edge e : graph.get(edge.node)) {
- if (!visited[e.node]) {
- pq.add(e);
- }
- }
- }
- return total;
- }
- }
These implementations show how the algorithm can be adapted in various programming languages while maintaining its core logic.
Real-world Applications of Prim’s Algorithm
Prim’s Algorithm has numerous practical applications:
- Network Design: Laying out the least-cost network of cables, roads, or pipelines.
- Computer Networking: Designing routing paths in switches and routers.
- Civil Engineering: Planning efficient road, rail, or electrical systems.
- Cluster Analysis: In data mining to connect components with minimal linkage cost.
- Gaming/Graphics: Creating mazes or connecting tiles with the lowest edge weight.
Its applicability wherever minimal connection cost is crucial makes it a staple in engineering and computer science.
Limitations and Edge Cases
Despite its efficiency, Prim’s Algorithm has some limitations:
- It only works on connected graphs. For disconnected graphs, it will leave out components.
- Negative edge weights are permissible, but must be handled carefully (no infinite loops).
- The starting node can influence the order of edge inclusion, though the final MST weight remains the same.
- On very large graphs, memory usage becomes critical if using adjacency matrices.
Edge cases like graphs with all edges of equal weight, duplicate edges, or dense graphs with high vertex count should be tested thoroughly to validate implementation stability.
Summary
Prim’s Algorithm is a greedy method for computing the minimum spanning tree of a weighted, undirected, connected graph. It expands the MST by always choosing the minimum weight edge that adds a new vertex. Using min-heaps and adjacency lists, Prim’s can operate efficiently even on large graphs. While Kruskal’s is better for sparse graphs, Prim’s is preferred for dense ones. To complement such graph optimization strategies with practical development expertise, exploring Web Developer Training equips learners with hands-on experience in HTML, CSS, JavaScript, and full-stack frameworks empowering them to build scalable web applications that integrate algorithmic efficiency with responsive design and real-world performance. Its wide range of real-world applications makes it an essential algorithm for computer scientists and engineers. Implementations in multiple programming languages further showcase its adaptability and efficiency.
