
- Introduction to Minimum Spanning Trees
- Overview of Kruskal’s Algorithm in DAA
- Graph Terminology (Vertices, Edges, Weights)
- Step-by-Step Explanation of Kruskal’s Algorithm
- Union-Find (Disjoint Set) Data Structure
- Pseudocode for Kruskal’s Algorithm in DAA
- Time and Space Complexity Analysis
- Implementation in C++/Java/Python
- Kruskal’s vs Prim’s Algorithm
- Applications of Kruskal’s Algorithm in Real Life
- Advantages and Limitations
- Summary
Introduction to Minimum Spanning Trees
In graph theory, a Minimum Spanning Tree (MST) is a subset of the edges in a connected, undirected, and weighted graph that connects all the vertices together, without any cycles, and with the minimum total edge weight. MSTs are crucial in various fields like computer networks, road construction planning, and circuit design, where connecting all components with minimal cost is the goal. To complement such optimization strategies with practical development expertise, exploring Web Developer Training equips learners with the skills to build efficient, scalable web applications covering HTML, CSS, JavaScript, and backend technologies that support structured logic, resource management, and performance-driven design.
To Earn Your Web Developer Certification, Gain Insights From Leading Web Developer Experts And Advance Your Career With ACTE’s Web Developer Courses Today!
Overview of Kruskal’s Algorithm in DAA
Kruskal’s Algorithm, proposed by Joseph Kruskal in 1956, is a greedy algorithm that finds a Minimum Spanning Tree for a graph. It works by sorting all the edges in ascending order of their weight and adding edges one by one to the MST, ensuring no cycles are formed. To complement such algorithmic precision with foundational object-oriented design, exploring Understanding Abstract Classes in C++ reveals how abstraction and pure virtual functions enable flexible, reusable architectures essential for implementing polymorphic behavior and scalable system logic.
Key Features:
- Greedy in nature.
- Efficient for sparse graphs.
- Requires cycle detection (using Union-Find).
Graph Terminology (Vertices, Edges, Weights)
Before diving into Kruskal’s Algorithm, it’s essential to understand the following graph terms: To complement such foundational graph concepts with performance analysis, exploring Asymptotic Notation provides the mathematical framework for evaluating algorithm efficiency highlighting Big O, Omega, and Theta notations that help compare time and space complexity across different graph traversal and optimization techniques.
- Vertex (Node): A point in the graph.
- Edge: A connection between two vertices.
- Weight: A numerical value assigned to an edge, representing cost or distance.
- Cycle: A path in which the starting and ending node is the same.
- Connected Graph: A graph in which there is a path between every pair of vertices.
In Minimum Spanning Tree (MST) problems, we deal with connected, undirected, weighted graphs.
Would You Like to Know More About Web Developer? Sign Up For Our Web Developer Courses Now!
Step-by-Step Explanation of Kruskal’s Algorithm
Steps in Kruskal’s Algorithm:
- Sort All Edges: Sort all the edges in the graph by their weights in ascending order.
- Initialize Disjoint Sets: Create a disjoint set for all vertices (initially, each vertex is in its own set).
- Pick the Smallest Edge: Start picking the smallest edge. Before adding it to the MST, check whether it forms a cycle using the Union-Find structure.
- Cycle Check: If the selected edge connects vertices from different sets, it doesn’t form a cycle and can be safely added to the MST.
- Repeat: Continue this process until the MST contains exactly (V – 1)edges, where V is the number of vertices.
- Output: Return the MST and its total cost.
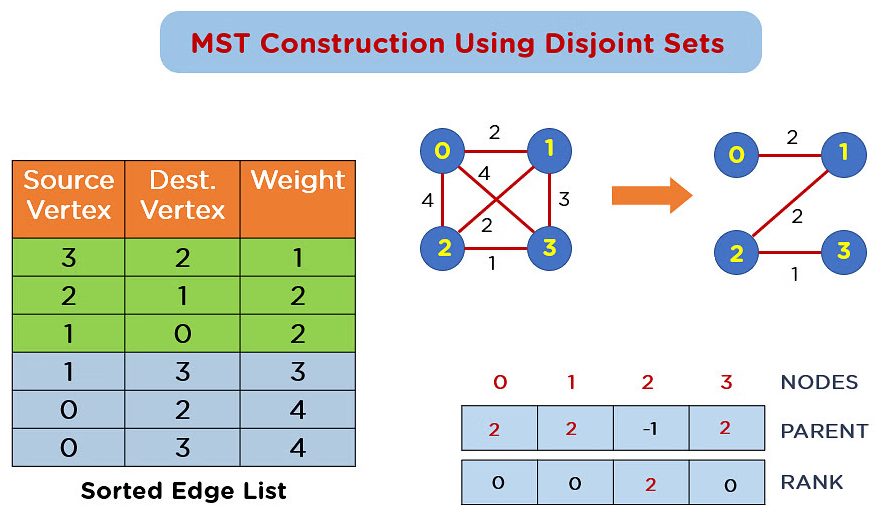
Union-Find (Disjoint Set) Data Structure
The Disjoint Set Union (DSU) or Union-Find data structure is an efficient way to manage and merge disjoint sets. The Find operation identifies the root representative of the set that contains a specific element. The Union operation merges the sets of two elements, ensuring they have the same root. To improve performance, two main optimizations are used. Path Compression is applied during the Find operation, allowing nodes to connect directly to their root. This significantly speeds up future queries. To complement such algorithmic efficiency with practical development expertise, exploring Web Developer Training equips learners with the skills to build high-performance web applications covering HTML, CSS, JavaScript, and backend technologies that support optimized data structures, scalable logic, and responsive user experiences. Additionally, Union by Rank or Size ensures that when merging sets, the smaller tree always attaches to the larger tree.
- parent = [i for i in range(n)]
- def find(x):
- if parent[x] != x:
- parent[x] = find(parent[x])
- return parent[x]
- def union(x, y):
- root_x = find(x)
- root_y = find(y)
- if root_x != root_y:
- parent[root_y] = root_x
Are You Interested in Learning More About Web Developer? Sign Up For Our Web Developer Courses Today!
Pseudocode for Kruskal’s Algorithm in DAA
Kruskal’s Algorithm in DAA
- KRUSKAL(G):
- MST = ∅
- for each vertex v in G:
- MAKE-SET(v)
- sort all edges in G by increasing weight
- for each edge (u, v) in sorted order:
- if FIND-SET(u) ≠ FIND-SET(v):
- MST = MST ∪ {(u, v)}
- UNION(u, v)
- return MST
This ensures that no cycles are formed while gradually constructing the minimum spanning tree.
Time and Space Complexity Analysis
Time Complexity:
- Sorting Edges: O(E log E), where E is the number of edges.
- Union-Find Operations: O(E × α(V)), where α is the inverse Ackermann function (almost constant time).
- O(E log E) or O(E log V) (since E ≈ V² in dense graphs)
Space Complexity:
- Storing edges: O(E)
- Disjoint Set arrays: O(V)
- So, Space Complexity: O(E + V)
Implementation in C++/Java/Python
C++ Implementation:
- struct Edge {
- int u, v, weight;
- bool operator<(Edge const& other) {
- return weight < other.weight;
- }
- };
- int find(int x, vector<int>& parent) {
- if (parent[x] != x)
- parent[x] = find(parent[x], parent);
- return parent[x];
- }
- void union_sets(int a, int b, vector<int>& parent) {
- a = find(a, parent);
- b = find(b, parent);
- if (a != b)
- parent[b] = a;
- }
- int kruskal(int n, vector<Edge>& edges) {
- sort(edges.begin(), edges.end());
- vector<int> parent(n);
- for (int i = 0; i < n; ++i)
- parent[i] = i;
- int mst_weight = 0;
- for (Edge e : edges) {
- if (find(e.u, parent) != find(e.v, parent)) {
- mst_weight += e.weight;
- union_sets(e.u, e.v, parent);
- }
- }
- return mst_weight;
- }
Java Implementation:
- class Edge implements Comparable<Edge> {
- int u, v, weight;
- public int compareTo(Edge other) {
- return this.weight – other.weight;
- }
- }
- int find(int[] parent, int x) {
- if (parent[x] != x)
- parent[x] = find(parent, parent[x]);
- return parent[x];
- }
- void union(int[] parent, int x, int y) {
- parent[find(parent, x)] = find(parent, y);
- }
- int kruskal(List<Edge> edges, int n) {
- Collections.sort(edges);
- int[] parent = new int[n];
- for (int i = 0; i < n; i++) parent[i] = i;
- int mstCost = 0;
- for (Edge e : edges) {
- if (find(parent, e.u) != find(parent, e.v)) {
- mstCost += e.weight;
- union(parent, e.u, e.v);
- }
- }
- return mstCost;
- }
Python Implementation:
- def find(parent, x):
- if parent[x] != x:
- parent[x] = find(parent, parent[x])
- return parent[x]
- def union(parent, x, y):
- parent[find(parent, x)] = find(parent, y)
- def kruskal(edges, n):
- edges.sort(key=lambda x: x[2])
- parent = [i for i in range(n)]
- mst_weight = 0
- for u, v, w in edges:
- if find(parent, u) != find(parent, v):
- union(parent, u, v)
- mst_weight += w
- return mst_weight
Kruskal’s vs Prim’s Algorithm
| Feature | Kruskal’s Algorithm | Prim’s Algorithm |
|---|---|---|
| Type | Edge-based | Vertex-based |
| Data Structure | Disjoint Set (Union-Find) | Priority Queue (Heap) |
| Best For | Sparse Graphs | Dense Graphs |
| Edge Sorting Needed | Yes | No |
| Starting Vertex | No (global edge min) | Yes (starts from a vertex) |
| Cycle Check | Union-Find | No explicit check needed |
Kruskal’s algorithm is generally more efficient for sparse graphs, while Prim’s algorithm is better for dense graphs due to its priority queue approach. To complement such algorithmic strategies with robust resource management, exploring Destructor in C++ reveals how automatic cleanup mechanisms like destructors ensure safe memory handling, prevent leaks, and support scalable system design especially in applications involving dynamic data structures and graph-based computations.
Applications of Kruskal’s Algorithm in Real Life
- Network Design: Used in designing efficient telecommunication, electrical, or computer networks with minimal cabling or wiring cost.
- Transportation Planning: Helps build efficient roadways, railway lines, or pipelines by connecting multiple locations with minimum total cost. To complement such optimization strategies with precise execution logic, exploring Control Statements Examples provides insight into how conditional structures like if-else, switch-case, and loops in C.
- Circuit Design: Used in VLSI design and computer chip manufacturing for optimal component connection.
- Clustering Algorithms: Forms part of hierarchical clustering techniques in data mining.
- Image Processing: In some algorithms, MSTs help in segmenting images by detecting edges and boundaries.
Advantages and Limitations
Advantages:
- Simple and intuitive. To complement such clarity in problem-solving, exploring Kadane’s Algorithm reveals how a single-pass strategy efficiently solves the maximum subarray problem leveraging dynamic programming to track cumulative sums.
- Works well for disconnected graphs (generates a minimum spanning forest).
- Efficient with sorting and Union-Find optimization.
Limitations:
- Not suitable for dense graphs with lots of edges.
- Requires sorting all edges before processing.
- Not adaptive always requires edge sorting even for small MST sizes.
Summary
Kruskal’s algorithm is a simple but powerful tool in graph theory. It is mainly used to find a Minimum Spanning Tree (MST). The algorithm works by sorting all the edges of a graph and adding them one at a time, making sure no cycles are created. To complement such graph-based optimization techniques with practical development expertise, exploring Web Developer Training equips learners with the skills to build efficient, scalable web applications covering HTML, CSS, JavaScript, and backend technologies that support structured logic, data flow, and performance-driven design. To check for cycles efficiently, Kruskal’s algorithm uses a Union-Find data structure. Its time complexity is O(E log E), which makes it particularly effective for sparse graphs with fewer edges compared to their vertices.





