
- Introduction to Data Compression
- What is Huffman Coding?
- Applications of Huffman Coding
- Frequency Table
- Steps to Construct Huffman Tree
- Priority Queue and Min-Heap Usage
- Encoding Process: How Characters Are Compressed
- Decoding Huffman Encoded Data
- Pseudocode and Flow Diagram
- Time and Space Complexity Analysis
- Real-World Use Cases
- Summary
Introduction to Data Compression
In the digital world, data compression is essential for reducing file size and optimizing storage and transmission efficiency. Data compression techniques aim to represent data using fewer bits without losing the original information. To complement such optimization strategies with practical development skills, exploring Web Developer Training equips learners with hands-on experience in HTML, CSS, JavaScript, and full-stack frameworks enabling them to build efficient, scalable web applications that integrate performance-conscious features like compressed assets and optimized data flow. There are two types of data compression:
- Lossless Compression: No data is lost (e.g., ZIP, PNG)
- Lossy Compression: Some data is lost, but the reduction is significant (e.g., JPEG, MP3)
Huffman Coding is a popular lossless compression algorithm based on frequency analysis of characters and is widely used in file compression, communication protocols, and data storage.
To Earn Your Web Developer Certification, Gain Insights From Leading Web Developer Experts And Advance Your Career With ACTE’s Web Developer Courses Today!
What is Huffman Coding?
Huffman Coding is a popular method for compressing data, first introduced by David A. Huffman in 1952. This algorithm effectively reduces the size of data by assigning shorter binary codes to characters that appear frequently, while less common characters receive longer codes. This approach is based on a greedy algorithm that creates a unique binary tree, ensuring that no code is a prefix of another, which allows for efficient decoding. To complement such algorithmic precision with performance validation under extreme conditions, exploring What is Spike Testing reveals how software systems respond to sudden surges or drops in user load helping developers assess recovery time, system resilience, and scalability during unpredictable traffic spikes. The most significant advantage of Huffman Coding is its ability to achieve optimal encoding based on the frequency of each character in the data set.
Applications of Huffman Coding
- File Compression: Formats like ZIP and GZIP reduce file size for storage and transmission.
- Multimedia Formats: JPEG image compression and MP3 audio compression optimize media storage and playback.
- Communication Protocols: Enables efficient bandwidth utilization by compressing transmitted data.
- Compiler Design: Token stream optimization improves parsing and memory usage.
- Data Storage: Reduces database or log file sizes for better performance and scalability.
- Embedded Systems: Supports compact storage in resource-constrained environments.
Its ability to reduce size without losing accuracy makes it ideal for systems requiring fidelity and efficiency.
Would You Like to Know More About Web Developer? Sign Up For Our Web Developer Courses Now!
Frequency Table
Frequency Table:
Each character in the input data is analyzed for how often it appears. This frequency guides how the codes are assigned. To complement such frequency-based encoding with career-oriented development insights, exploring Full Stack Developer Salary reveals earning potential across experience levels, tech stacks, and geographic regions helping professionals understand how versatile skills in both front-end and back-end development translate into competitive compensation packages.
Example Input: `aabcccddddd`
- a: 2
- b: 1
- c: 3
- d: 5
- [d:5]
- [c:3]
- [a:2]
- [b:1]
- Replace each character in the input with its binary code.
- Concatenate all codes to form the final encoded bitstream.
- a: 110
- b: 111
- c: 10
- d: 0
- 1101101111010100000
- Start at the root of the tree.
- Read a ‘0’: go left; Read a ‘1’: go right.
- When a leaf node is reached, decode the character.
- Repeat from root for the next sequence of bits.
- 110 → a
- 110 → a
- 111 → b
- 10 → c
- 10 → c
- 0 → d
- function buildHuffmanTree(charFreqs):
- Initialize priorityQueue with all characters
- while priorityQueue.size > 1:
- left = priorityQueue.pop()
- right = priorityQueue.pop()
- newNode = Node(left.freq + right.freq, left, right)
- priorityQueue.push(newNode)
- return priorityQueue.pop() // Root of Huffman Tree
- function generateCodes(node, code):
- if node is leaf:
- store code for character
- generateCodes(node.left, code + “0”)
- generateCodes(node.right, code + “1”)
- Input Text → Frequency Table → Min-Heap
- Build Tree (merge nodes)
- Generate Binary Codes
- Encode Input → Binary Output
- Building Frequency Table: O(n) where n is the total number of characters.
- Building Min-Heap: O(d log d) where d is the number of unique characters.
- Merging Heap Nodes: O(d log d) combining nodes to construct the Huffman tree.
- Traversing Tree to Generate Codes: O(d) each unique character is assigned a code.
- Total Time Complexity: O(n + d log d)
- Frequency Table: O(d) space required to store frequencies of distinct characters.
- Huffman Tree: O(d) space needed to build and store the binary tree structure.
- Encoded Data: Depends on entropy, worst-case O(n) where n is the input length.
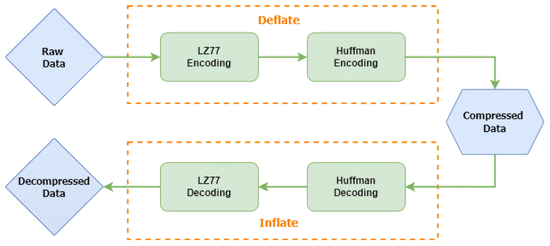
- ZIP File Compression: Uses Huffman coding (alongside LZ77) to reduce file sizes while preserving content.
- JPEG Image Compression: Applies Huffman coding after Discrete Cosine Transform (DCT) and quantization, effectively compressing image data.
- MP3 Audio Compression: Uses Huffman coding to encode frequency domain data after psychoacoustic modeling and quantization.
- PDF and PostScript: Compress text streams and fonts using Huffman-based encoders.
- Embedded Systems: Used for storing large character tables or logs efficiently.
Steps to Construct Huffman Tree
To construct a Huffman Tree for encoding characters based on their frequencies, follow these straightforward steps. First, build a frequency table to count how often each character appears. For each unique character, create a leaf node. Next, insert these leaf nodes into a min-heap, which is sorted by frequency. To complement such algorithmic precision with practical development skills, exploring Web Developer Training equips learners with hands-on experience in HTML, CSS, JavaScript, and full-stack frameworks empowering them to build efficient, scalable web applications that integrate performance-conscious features like compressed assets and optimized data structures. As long as the heap contains more than one node, combine the two nodes with the lowest frequencies to form a new internal node, then insert this new node back into the heap. Once the tree is built, generate binary codes by traversing from the root to each leaf. As you move to the left, add a ‘0’ to the code, while a right move adds a ‘1’. The paths to the leaf nodes will give you the unique codes for each character, effectively compressing the data based on frequency.
Are You Interested in Learning More About Web Developer? Sign Up For Our Web Developer Courses Today!
Priority Queue and Min-Heap Usage
To efficiently manage the merging of the lowest frequency nodes, a priority queue (min-heap) is used. This ensures efficient retrieval of the two nodes with the lowest frequency (O(log n)) and fast insertion of merged nodes back into the queue. This makes the algorithm both efficient and scalable for large datasets. To complement such data-driven optimization with structured service communication, exploring What is WSDL in Web Services explains how WSDL acts as a formal contract between client and server defining available operations, data types, and message formats for seamless integration across distributed systems.
Sample Min-Heap:
Merging continues until a single tree remains.
Encoding Process: How Characters Are Compressed
Merging continues until a single tree remains. After generating binary codes from the Huffman tree, each symbol is assigned a unique prefix-free code based on its frequency. To complement such algorithmic encoding with real-time data acquisition and control, exploring Virtual Instrumentation using Labview reveals how engineers can build custom graphical interfaces, automate measurements, and simulate instrumentation workflows leveraging LabVIEW’s dataflow programming to visualize, process, and analyze signals with precision.
Example:
This output is significantly shorter than using 8-bit ASCII encoding.
Decoding Huffman Encoded Data
Decoding requires the same Huffman tree used for encoding. The decoder reads bits one by one: traversing the tree until it reaches a leaf node that maps to a character. To complement such structured decoding logic with efficient build automation, exploring Gradle vs Maven offers a detailed comparison of two powerful Java build tools highlighting Gradle’s flexibility and performance through Groovy-based scripts versus Maven’s convention-driven simplicity and robust dependency management.
Example: Input bits: `110110111…`
Decoding continues until the entire bitstream is converted.
Pseudocode and Flow Diagram
Pseudocode:
Flow Diagram:
Time and Space Complexity Analysis
Time Complexity:
Space Complexity:
Here, n is the input length and d is the number of distinct characters. To complement such complexity analysis with controlled execution timing, exploring Python Sleep Method reveals how developers can pause thread execution using `time.sleep()` enabling precise delays, dramatic output pacing, and synchronized multithreaded operations in Python applications.
Real-World Use Cases
Summary
Huffman Coding is a commonly used method for lossless data compression. It creates a binary tree based on how often characters appear in a dataset. Characters that occur more frequently get shorter codes, helping to reduce the data size. This algorithm uses priority queues to make the tree-building process faster, which is effective for compressing different types of data, including text and multimedia. While Huffman Coding works well in many situations, such as ZIP files, JPEG images, and MP3 audio, it has some limitations. For example, it requires two passes: one to build the frequency table and another to encode the data. To complement such compression techniques with practical development skills, exploring Web Developer Training equips learners with hands-on experience in HTML, CSS, JavaScript, and full-stack frameworks empowering them to build efficient, scalable web applications that integrate seamlessly with backend logic and data optimization strategies. one to build a frequency table and another to encode the data. It may not be the best choice for small datasets or when characters are evenly distributed. In addition, the Huffman tree or codebook needs to be stored with the compressed data, and its effectiveness goes down when character frequencies are similar.





