
- What is Flood Fill Algorithm?
- Applications in Graphics and Games
- 4-way vs 8-way Flood Fill
- Recursive Approach
- Iterative Stack-based Approach
- Color Replacement Logic
- Algorithm Pseudocode
- Conclusion
What is Flood Fill Algorithm?
The Flood Fill algorithm is a region-filling algorithm commonly used in computer graphics to determine and alter the area connected to a given node in a multi-dimensional array. Think of it as the digital equivalent of the “paint bucket” tool found in image editing software. It works by replacing a target color in a bounded area with a new color starting from a seed point and spreading outward. Flood Fill plays a vital role in image processing, coloring regions in GUIs, Web Designing & Development Training and solving problems in grid-based games like Minesweeper or Sudoku. It’s fundamentally a traversal technique usually implemented via recursion or stack that visits and updates connected pixels. The Flood Fill algorithm is a graph traversal method used to determine and alter the area connected to a given node in a multi-dimensional array. It’s most commonly known from paint programs like the “bucket fill” tool that fills a contiguous area of the same color with a new color. Flood fill works by starting at a seed point (usually a pixel or cell) and recursively or iteratively spreading out to adjacent points that meet a specific condition, such as having the same color or value. It continues this process until it reaches boundaries where the condition fails.
To Earn Your Web Developer Certification, Gain Insights From Leading Data Science Experts And Advance Your Career With ACTE’s Web Developer Courses Today!
Applications in Graphics and Games
Flood Fill is integral to several real-world and interactive applications:
- Image Editors: The “bucket fill” tool fills a bounded area with a chosen color.
- Drawing Applications: Used to fill shapes or polygons with patterns or colors.
- Game Development: In tile-based games, to detect and fill connected components. To highlight contiguous game zones or mark map boundaries Software Developer vs Software Engineer.
- Maze Solvers and Pathfinders: Filling reachable areas from a point to visualize reachability.
- Pattern Recognition: Used to identify and mark clusters in images or arrays.
- Medical Imaging and CAD tools: Useful in segmentation and region marking.
4-way vs 8-way Flood Fill
Flood Fill algorithms can be classified based on how they define adjacency between cells or pixels. The two most common types are 4-way and 8-way Flood Fill.
4-Way Flood Fill
- (x-1, y) → left
- (x+1, y) → right
- (x, y-1) → up
- (x, y+1) → down
- Simpler and faster in many grid-based applications.
- Less prone to “bleeding” into diagonally adjacent regions.
- (x-1, y-1) → top-left
- (x+1, y-1) → top-right
- (x-1, y+1) → bottom-left
- (x+1, y+1) → bottom-right
- More complete fill in natural or organic shapes.
- Covers diagonally connected areas seamlessly.
- Check if the current pixel is within bounds.
- If it has the original color, replace it with the new color.
- Recur for all valid neighbors (4 or 8 directions).
- Complete Guide on System Software May cause stack overflow for large areas due to deep recursion.
- Not suitable for real-time applications unless properly controlled.
- Uses an explicit stack (LIFO) to simulate recursion and avoid stack overflow.
- Begins from the seed/start cell, which is pushed onto the stack.
- Pop the top cell.
- Check if it’s valid (within bounds and matches target condition/color).
- Update the cell (e.g., change color or mark as visited).
- Best Software Development Courses Push all valid neighboring cells (4-way or 8-way) onto the stack.
- Avoids recursion limits, making it safer for large grids.
- Ideal for Depth-First Search (DFS) style exploration.
- Can be optimized with a visited set or by modifying the grid in place.
- Slower than BFS in some cases but uses less memory than recursive DFS in deep graphs.
- function floodFill(x, y, originalColor, newColor):
- if (x < 0 or x >= width or y < 0 or y >= height):
- return
- if (pixel[x][y] ≠ originalColor):
- return
- pixel[x][y] = newColor
- floodFill(x+1, y, originalColor, newColor)
- floodFill(x-1, y, originalColor, newColor)
- floodFill(x, y+1, originalColor, newColor)
- floodFill(x, y-1, originalColor, newColor)
Adjacency Considered: Only four directions – up, down, left, and right.
Coordinates Checked:
Use Case: IT Engineer Salary in India When diagonal movement is not allowed or not meaningful (e.g., filling a rectangular grid like in maze solving).
Advantages:
8-Way Flood Fill
Adjacency Considered: All eight directions – up, down, left, right, and the four diagonals.
Coordinates Checked:
All from 4-way plus:
Use Case: When diagonal adjacency should be included (e.g., in image processing or pixel-based applications).
Advantages:
Would You Like to Know More About Web Developer? Sign Up For Our Web Developer Courses Now!
Recursive Approach
Recursive flood fill is the most intuitive implementation. It checks the current pixel and recursively calls itself on neighboring pixels that match the original color. The recursive approach to Flood Fill uses Depth-First Search (DFS) to explore connected cells. Starting from a seed point, it checks if the current cell meets the condition (e.g., target color), changes its value, and recursively calls the function on neighboring cells. In 4-way flood fill, the function recurses in four directions (up, down, left, right), while in 8-way, Web Designing & Development Training it includes diagonals. A base case ensures the function stops when out of bounds or when the cell doesn’t match the target. Though simple and elegant, this approach can cause stack overflow on large grids without optimization.
Steps:
Limitations:
Iterative Stack-based Approach
While the stack is not empty:
Are You Interested in Learning More About Web Developer? Sign Up For Our Web Developer Courses Today!
Color Replacement Logic
The color replacement logic is the core component of the flood fill algorithm, responsible for identifying and updating all connected cells that share the same initial color. The process begins by capturing the target color at the starting point (seed coordinates). Before any filling occurs, it’s crucial to check if the target color and the replacement color are the same. If they are, the algorithm should exit immediately to prevent unnecessary work or infinite loops. During traversal, Become an IT Engineer whether recursive or iterative, each cell is evaluated to ensure it is within bounds and matches the target color. If both conditions are met, the cell’s color is changed to the replacement color.
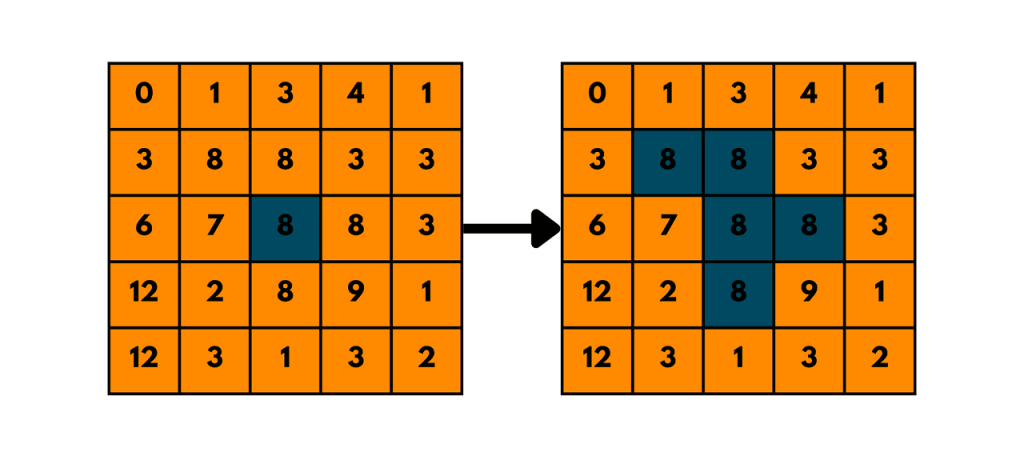
The algorithm then proceeds to its neighboring cells (in either 4-way or 8-way directions), applying the same checks and replacements. This process continues until all connected cells of the original color have been filled. This logic ensures that only the region connected to the starting cell and having the same original color is updated, preventing “bleeding” into other areas and maintaining fill boundaries. Proper boundary checks and early exit conditions are essential for both correctness and performance.
Algorithm Pseudocode
Recursive 4-Way Flood Fill:
Conclusion
The Flood Fill algorithm is a powerful tool in computer graphics, from simple shape coloring to complex region analysis. While the recursive approach is easy to implement, the iterative method is preferred for robustness and performance. Understanding the principles of neighborhood traversal, color replacement, Web Designing & Development Training and boundary handling equips you to use this algorithm in a wide range of applications from gaming to image analysis. Whether you’re building a paint application or a grid-based puzzle solver,Pseudocode mastering flood fill gives you a strong foundation in both graphics and algorithmic logic.





