Bubble Sort Algorithm in C with Example Code

Introduction to Bubble Sort

Bubble Sort is a foundational algorithm in the world of computer science, known for its simplicity and pedagogical value. It is one of the earliest algorithms taught to students because it clearly illustrates the concept of sorting. In Bubble Sort, the algorithm repeatedly steps through the list, compares adjacent elements, and swaps them if they are in the wrong order. This repetitive process continues until the list is sorted, with the largest unsorted element ‘bubbling’ up to its correct position at the end of the list during each iteration. Although Bubble Sort is not suitable for large datasets due to its inefficiency, its conceptual simplicity makes it ideal for introductory learning. Understanding Bubble Sort also lays the groundwork for grasping more advanced sorting techniques like Merge Sort and Quick Sort Web Designing & Development Training. Bubble Sort is one of the simplest and most well-known sorting algorithms in computer science. It works by repeatedly stepping through a list of elements, comparing adjacent pairs, and swapping them if they are in the wrong order. This process continues until the entire list is sorted. The algorithm gets its name because smaller elements “bubble” to the top (beginning) of the list with each pass. Despite its simplicity, Bubble Sort is not efficient for large datasets due to its high time complexity O(n²) in the worst and average cases. However, it is often used for educational purposes to teach the fundamentals of sorting and algorithmic thinking. One of the advantages of Bubble Sort is that it is easy to implement and understand, making it a good starting point for beginners learning data structures and algorithms. An optimized version of Bubble Sort includes a flag to detect whether any swaps were made during a pass. If no swaps occur, the list is already sorted, and the algorithm can terminate early, improving efficiency slightly in best-case scenarios. In summary, while Bubble Sort is not ideal for performance-critical applications, it is an important foundational algorithm for learning how sorting works.

To Earn Your Web Developer Certification, Gain Insights From Leading Data Science Experts And Advance Your Career With ACTE’s Web Developer Courses Today!

Working Principle

• The fundamental principle of Bubble Sort revolves around comparing adjacent elements and swapping them if they are not in the desired order, typically ascending or descending.
• During each pass through the array, the highest unsorted value is moved to its correct position, much like bubbles rising to the surface, hence the name. This process is repeated for the entire list until no further swaps are necessary.
• Each complete pass through the array guarantees that at least one more element is correctly positioned. This guarantees that the array becomes increasingly sorted with each iteration.
• Despite its inefficiency for large datasets, the concept is intuitive and offers a hands-on approach to understanding basic algorithmic logic and iteration Minimum Spanning Tree.
• The working principle of Bubble Sort is based on repeatedly comparing and swapping adjacent elements in a list to move larger elements toward the end.
• In each pass through the array, the algorithm compares each pair of adjacent elements. If the current element is greater than the next one, they are swapped. This process continues from the beginning to the end of the array.
• After the first pass, the largest element settles at its correct position at the end. The algorithm then repeats the same process for the remaining unsorted portion of the list.



• This continues until no more swaps are needed, indicating that the list is sorted. In the best case (already sorted list), an optimized version of Bubble Sort can detect no swaps and exit early.
• While easy to understand and implement, Bubble Sort is inefficient for large datasets due to its O(n²) time complexity in the average and worst cases.

Subscribe To Contact Course Advisor

Subscribe

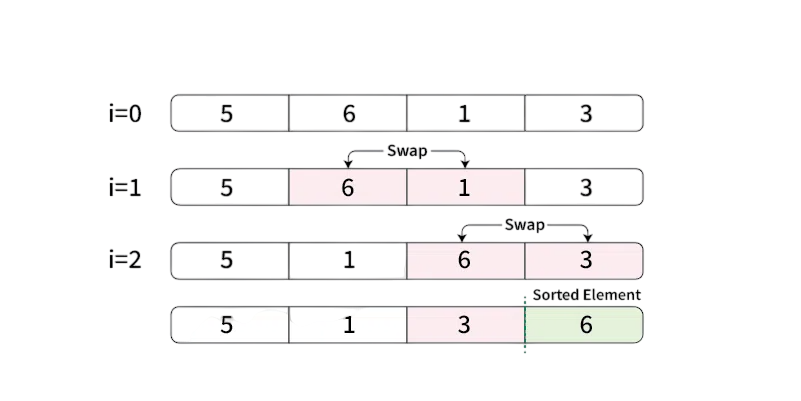
Algorithm Explanation

The Bubble Sort algorithm consists of two nested loops. The outer loop ensures that the process is repeated enough times to sort the entire array, while the inner loop performs the pairwise comparisons and swaps for each pass GUI Tkinter Module. Here is a breakdown of the algorithm:

• Start with the first element in the array.
• Compare the current element with the next one.
• If the current element is greater than the next (assuming ascending order), swap them.
• Move to the next pair and repeat until the end of the array is reached.
• Repeat the entire process for n-1 passes, where n is the number of elements in the array.
• With each pass, the largest unsorted element moves to its correct position.

This method continues until a complete pass is made without any swaps, indicating that the array is sorted.

Would You Like to Know More About Web Developer? Sign Up For Our Web Developer Courses Now!

Flowchart and Pseudocode

Understanding Bubble Sort through a flowchart helps visualize the flow of control through the nested loops and conditionals Web Designing & Development Training. Here’s a high-level pseudocode representation of Bubble Sort:

procedure bubbleSort(A: list of sortable items)

• n = length(A)
• for i from 0 to n-1 do:
• for j from 0 to n-i-2 do:
• if A[j] > A[j+1] then
• swap A[j] and A[j+1]

This pseudocode reflects the essential logic of Bubble Sort, emphasizing the nested loops and the condition for swapping.

Develop Your Skills with Web Developer Certification Course

Weekday / Weekend BatchesSee Batch Details

Bubble Sort Code in C

Here’s a basic implementation of Bubble Sort in the C programming language Reverse C++ Vector :

• #include
• void bubbleSort(int arr[], int n) {
• for (int i = 0; i < n - 1; i++) {
• for (int j = 0; j < n - i - 1; j++) {
• if (arr[j] > arr[j + 1]) {
• int temp = arr[j];
• arr[j] = arr[j + 1];
• arr[j + 1] = temp;
• }
• }
• }
• }
• void printArray(int arr[], int n) {
• for (int i = 0; i < n; i++) {
• printf(“%d “, arr[i]);
• }
• printf(“\n”);
• }
• int main() {
• int arr[] = {64, 34, 25, 12, 22, 11, 90};
• int n = sizeof(arr)/sizeof(arr[0]);
• bubbleSort(arr, n);
• printf(“Sorted array: \n”);
• printArray(arr, n);
• return 0;
• }

Are You Interested in Learning More About Web Developer? Sign Up For Our Web Developer Courses Today!

Step-by-Step Execution Example

Let’s walk through an example to understand how Bubble Sort works step-by-step using the array [5, 1, 4, 2, 8]:

Pass 1:

• Compare 5 and 1 => swap => [1, 5, 4, 2, 8]
• Compare 5 and 4 => swap => [1, 4, 5, 2, 8]
• Compare 5 and 2 => swap => [1, 4, 2, 5, 8]
• Compare 5 and 8 => no swap

Pass 2:

• Compare 1 and 4 => no swap
• Compare 4 and 2 => swap => [1, 2, 4, 5, 8]
• Compare 4 and 5 => no swap

Pass 3:

• Compare 1 and 2 => no swap
• Compare 2 and 4 => no swap

Pass 4:

• No swaps needed. The array is sorted: [1, 2, 4, 5, 8]

Time and Space Complexity

• Best Case: O(n): In the best case, the array is already sorted. An optimized version of Bubble Sort can detect that no swaps are needed and terminate early Data Structures & Algorithms. Only one pass through the array is required, making the time complexity linear O(n).



• Average Case: O(n²): In most typical scenarios, the array elements are in random order. Bubble Sort must make multiple passes through the array, comparing each element with its neighbor in nested loops. This repeated process results in a quadratic time complexity O(n²).
• Worst Case: O(n²): The worst case occurs when the array is sorted in reverse order. Every pair of adjacent elements must be compared and swapped in each pass. This leads to the maximum number of operations, resulting in a time complexity of O(n²).

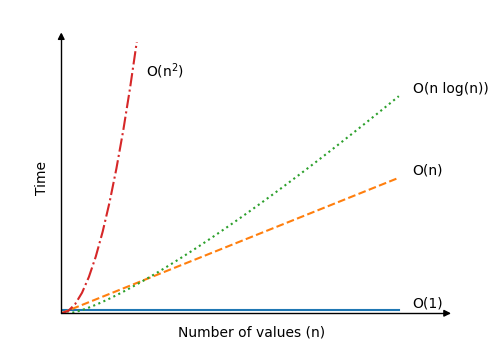
Best, Average, and Worst Case

• Best Case: When the array is already sorted in ascending order, Bubble Sort performs optimally. It makes a single pass through the array and detects that no swaps are necessary. With an optimized implementation that includes a flag to check for swaps, the algorithm can terminate early. In this scenario, the time complexity is O(n).
• Average Case: In the average case, where array elements are arranged in a random order, Bubble Sort performs multiple passes through the list Paging in Operating Systems. It compares and swaps many adjacent elements to gradually sort the array. Due to the nested loop structure, the number of operations increases significantly. As a result, the time complexity is O(n²).
• Worst Case: The worst-case scenario occurs when the array is sorted in reverse (descending) order. Bubble Sort must compare and swap every adjacent pair in each pass, resulting in the highest number of comparisons and swaps. This leads to maximum processing time, and the time complexity in this case is O(n²).

Web Development Sample Resumes! Download & Edit, Get Noticed by Top Employers! Download

Conclusion

Bubble Sort Code , though not efficient for large-scale applications, is an excellent algorithm for learning purposes. It introduces key programming concepts such as iteration, comparison, swapping, and control structures. The simplicity of Bubble Sort makes it easy to implement and understand. Through its stable and in-place sorting behavior, it lays a strong foundation for understanding more complex algorithms Web Designing & Development Training . Optimized versions make it slightly more practical for certain scenarios, but for real-world applications involving large datasets, algorithms like Merge Sort, Quick Sort, Time and Space Complexity and Heap Sort are generally preferred. Nevertheless, mastering Bubble Sort remains an essential milestone for every aspiring programmer or computer science student.