
- Introduction to Fibonacci Series
- Mathematical Definition of the Fibonacci Sequence
- Importance and Applications of Fibonacci Numbers
- Generating Fibonacci Series Using Loop
- Recursive Approach to Fibonacci Series in Python
- Using Memoization to Optimize Recursive Fibonacci
- Dynamic Programming Approach
- Generating Fibonacci Series Using Python Generators
- Printing Fibonacci Series up to a Given Number
- Real-world Examples
- Best Practices
- Summary
Introduction to Fibonacci Series
The Fibonacci series is one of the most classic sequences in mathematics and computer science. Starting with 0 and 1, each subsequent number is the sum of the two preceding numbers. The simplicity of this definition and the rich mathematical structure have made the Fibonacci sequence a staple in algorithmic problem-solving. To complement such foundational logic with practical development expertise, exploring Web Developer Training equips learners with hands-on experience in HTML, CSS, JavaScript, and full-stack frameworks empowering them to build responsive, scalable web applications that integrate algorithmic efficiency with user-centric design.
To Earn Your Web Developer Certification, Gain Insights From Leading Web Developer Experts And Advance Your Career With ACTE’s Web Developer Courses Today!
Mathematical Definition of the Fibonacci Sequence
The Fibonacci sequence is defined by the recurrence relation: each term is the sum of the two preceding ones, starting from 0 and 1. To complement such recursive logic with efficient execution and concurrency support, exploring Go Programming Language reveals how developers can leverage Goroutines, static typing, and a powerful standard library to implement scalable algorithms with minimal memory overhead and fast compile times.
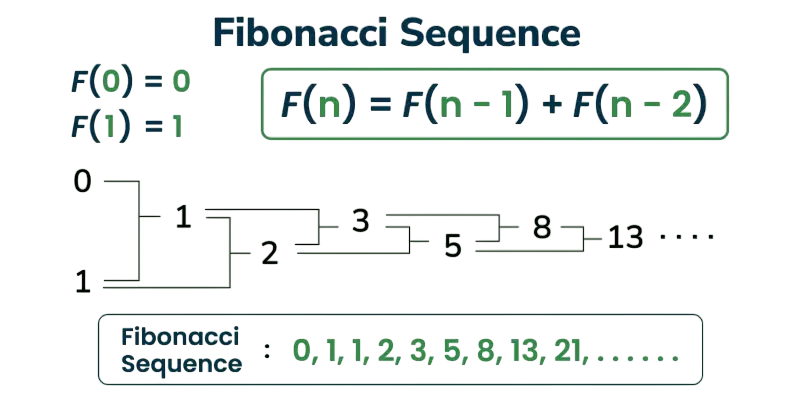
- $$
- F(n) =
- \begin{cases}
- 0 & \text{if } n = 0 \\
- 1 & \text{if } n = 1 \\
- F(n-1) + F(n-2) & \text{if } n > 1
- \end{cases}
- $$
This simple recurrence lays the foundation for many algorithmic implementations.
Importance and Applications of Fibonacci Numbers
Fibonacci numbers occur in numerous natural phenomena and computer science problems: from modeling population growth to optimizing recursive algorithms. To complement such mathematical patterns with structured programming control, exploring Python Scopes and Their Built-in Functions reveals how variable visibility and namespace management across global, local, enclosing, and built-in scopes enable developers to write clean, efficient, and bug-resistant Python code.
- Nature: Spiral arrangements in sunflowers, pinecones, and shells.
- Mathematics: Number theory, golden ratio (Φ ≈ 1.618), Pascal’s triangle.
- Computer Algorithms: Divide-and-conquer, dynamic programming, tree recursion.
- Technical Interviews: Commonly asked questions to test recursion and optimization.
- Financial Markets: Fibonacci retracement levels in trading.
- def fibonacci_iterative(n):
- a, b = 0, 1
- for _ in range(n):
- print(a, end=” “)
- a, b = b, a + b
- def fibonacci_recursive(n):
- if n <= 1:
- return n
- return fibonacci_recursive(n – 1) + fibonacci_recursive(n – 2)
- # Print first 10 Fibonacci numbers
- for i in range(10):
- print(fibonacci_recursive(i), end=” “)
- def fibonacci_memo(n, memo={}):
- if n in memo:
- return memo[n]
- if n <= 1:
- return n
- memo[n] = fibonacci_memo(n – 1, memo) + fibonacci_memo(n – 2, memo)
- return memo[n]
- # Print first 10 Fibonacci numbers
- for i in range(10):
- print(fibonacci_memo(i), end=” “)
- def fibonacci_dp(n):
- if n == 0:
- return [0]
- fib = [0, 1]
- for i in range(2, n):
- fib.append(fib[i – 1] + fib[i – 2])
- return fib
- # Print first 10 Fibonacci numbers
- print(fibonacci_dp(10))
- def fibonacci_generator():
- a, b = 0, 1
- while True:
- yield a
- a, b = b, a + b
- # Print first 10 Fibonacci numbers
- gen = fibonacci_generator()
- for _ in range(10):
- print(next(gen), end=” “)
- def fibonacci_upto_n(max_val):
- a, b = 0, 1
- while a <= max_val:
- print(a, end=” “)
- a, b = b, a + b
- # Print all Fibonacci numbers <= 100
- fibonacci_upto_n(100)
- Algorithm Design: Fibonacci is often a foundational concept for understanding recursion and dynamic programming.
- Financial Modeling: Fibonacci retracement levels are used in technical analysis of stocks.
- Nature and Art: Fibonacci spirals occur in galaxies, flowers, and seashells. The golden ratio derived from Fibonacci is used in architecture and design.
- Cryptography: Some encryption techniques explore Fibonacci patterns for key generation or transformation.
- Computer Graphics: Fractal patterns based on Fibonacci ratios appear in visual simulations and generative art.
- Use iterative or generator approaches in real applications.
- Apply memoization for recursive problems in competitive programming.
- Avoid excessive recursion due to stack overflow risks.
- Understand the use case before selecting the method (e.g., fixed size vs unknown limit).
- Analyze complexity when solving Fibonacci-based interview problems.
Would You Like to Know More About Web Developer? Sign Up For Our Web Developer Courses Now!
Generating Fibonacci Series Using Loop
The most straightforward way to generate a Fibonacci sequence is via a loop: iteratively updating two variables to track the current and next values.
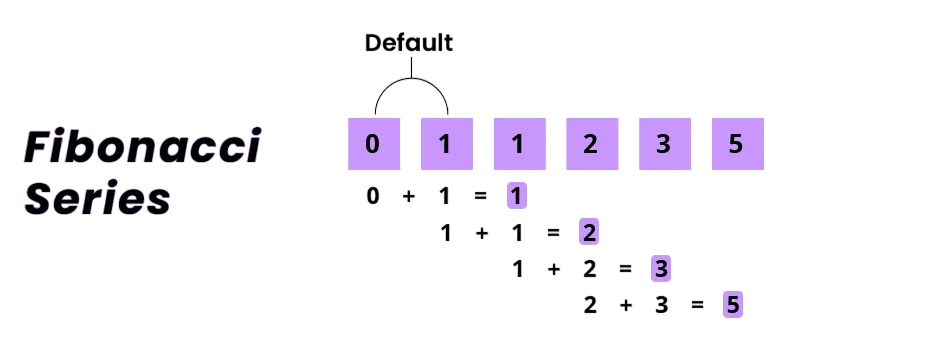
To complement such iterative logic with clean output presentation, exploring Python String Formatting reveals multiple techniques such as old-style `%` formatting, `str.format()`, and f-strings that allow developers to display numerical sequences, align values, and embed expressions with clarity and precision.
Recursive Approach to Fibonacci Series in Python
A direct implementation based on the mathematical recurrence: While such recursive logic forms the backbone of many algorithmic solutions, exploring Web Developer Training equips learners with practical skills in HTML, CSS, JavaScript, and full-stack frameworks empowering them to apply algorithmic thinking in building responsive, performance-optimized web applications that integrate both logic and design.
Are You Interested in Learning More About Web Developer? Sign Up For Our Web Developer Courses Today!
Using Memoization to Optimize Recursive Fibonacci
Memoization caches results of function calls to avoid recomputation: a technique that significantly improves performance in recursive algorithms by storing previously computed values. To complement such optimization strategies with persistent data handling, exploring Python Serialization reveals how objects and data structures can be converted into storable formats using modules like `pickle`, `json`, and `shelve` enabling efficient reuse, transfer, and long-term storage of computational results.
Dynamic Programming Approach
This uses bottom-up tabulation (iterative with a list):
Generating Fibonacci Series Using Python Generators
Python generators provide memory-efficient streaming of Fibonacci numbers: yielding one value at a time without storing the entire sequence in memory. To complement such runtime efficiency with robust application development capabilities, exploring What is .Net FrameWork offers insights into Microsoft’s comprehensive platform for building Windows-based applications featuring a rich class library, language interoperability, and powerful runtime services for scalable desktop and web solutions.
Printing Fibonacci Series up to a Given Number
You can generate Fibonacci numbers up to a limit value (e.g., all < 100): by iteratively updating two variables and checking each result against the threshold. To complement such controlled logic with process-driven development standards, exploring What is Quality Assurance explains how systematic procedures, testing protocols, and lifecycle audits ensure that software products meet defined quality benchmarks minimizing defects and enhancing reliability across production environments.
Real-World Examples
Best Practices:
Summary
The Fibonacci sequence starts with 0 and 1. Each new number is the sum of the two before it. You can implement this sequence in different ways, such as iterative, recursive, memoized, dynamic programming (DP), and generator methods. The recursive method is easy to understand, but it can be slow for bigger inputs because it repeats calculations. To complement such algorithmic simplicity with practical development expertise, exploring Web Developer Training equips learners with hands-on experience in HTML, CSS, JavaScript, and full-stack frameworks empowering them to build efficient, scalable web applications that minimize redundant operations and optimize performance across client-server interactions. To improve performance, use memoization or dynamic programming. These methods save previously calculated values to avoid doing the same work again. This speeds things up and makes them more efficient. Generators are a great option for large sequences.





