
- What is Graph Traversal?
- Graph Terminology Overview
- Breadth-First Search (BFS)
- Depth-First Search (DFS)
- Differences Between BFS and DFS
- Recursive vs Iterative Implementations
- Graph Representation (Adjacency List/Matrix)
- Applications of Graph Traversal
- Directed vs Undirected Graphs
- Graph Traversal Challenges
- Summary
What is Graph Traversal?
Graph traversal refers to the process of visiting, checking, and updating every vertex in a graph data structure. Traversing a graph allows us to process or search through all the nodes and their connections in a logical sequence. This concept is foundational in computer science and is used in numerous applications like route planning, social networks, and network analysis. To complement these algorithmic foundations with practical development expertise, exploring Web Developer Training reveals how mastering technologies like JavaScript, React, and backend frameworks equips professionals to build interactive web applications often integrating graph-based logic for features like dynamic routing, recommendation systems, and data visualization. There are two primary methods of graph traversal: Breadth-First Search (BFS) and Depth-First Search (DFS), each with unique strategies for visiting graph elements.
To Earn Your Web Developer Certification, Gain Insights From Leading Web Developer Experts And Advance Your Career With ACTE’s Web Developer Courses Today!
Graph Terminology Overview
Before exploring traversal methods, it’s important to understand some basic graph concepts. The first term is Vertex or Node, which represents a single unit in a graph that contains data. Next, we have an Edge, which is a line that connects two vertices. When two vertices are directly connected by an edge, they are called Adjacent.
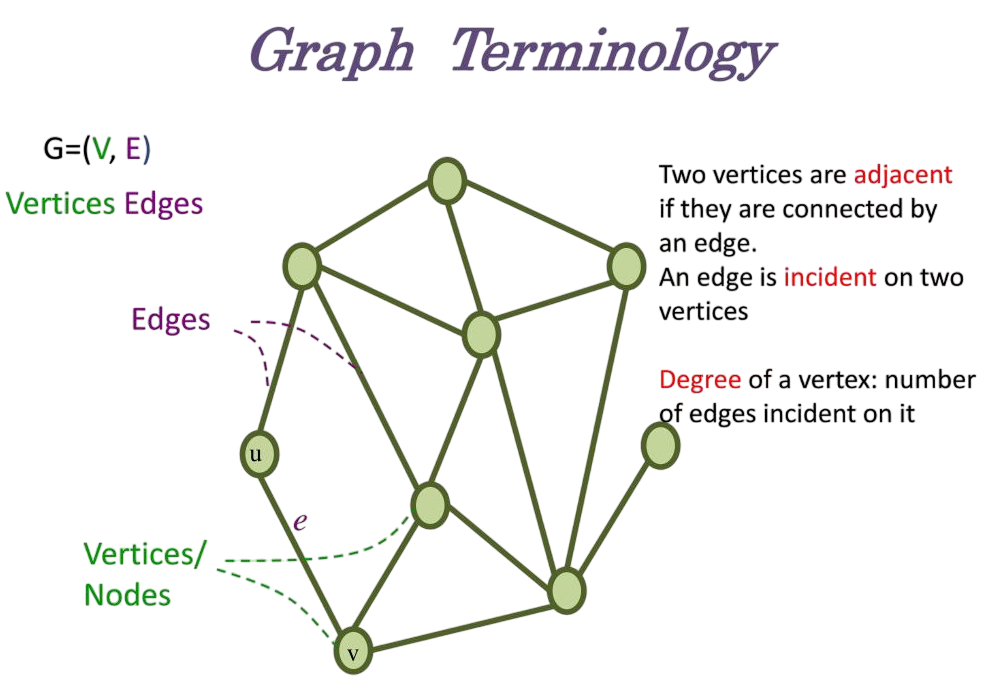
The Degree of a vertex shows how many edges are connected to it. A Path refers to a sequence of vertices connected by edges, while a Cycle is a special type of path that begins and ends at the same vertex. To complement these graph theory fundamentals with practical coding techniques, exploring Data Structures and Algorithms in Python reveals how Python’s built-in and user-defined structures like lists, sets, trees, and graphs enable efficient traversal, manipulation, and problem-solving across real-world applications. A Connected Graph means there is a path between every pair of vertices, ensuring all parts of the graph are reachable. Lastly, graphs can be Directed, where edges have a specific direction, or Undirected, where edges have no direction. Understanding these terms will provide a solid foundation for diving deeper into graph traversal methods.
Breadth-First Search (BFS)
- Breadth-First Search is a traversal method that explores all neighbor nodes at the present depth before moving on to nodes at the next depth level. It uses a queue data structure to keep track of the vertices that need to be explored next. BFS starts from a source node and visits all of its adjacent vertices. Then, it moves to the next level, visiting neighbors of the nodes that were just visited.
- Breadth-First Search (BFS) is a simple algorithm for exploring graphs. First, choose the source node and mark it as visited. Then, enqueue this node to keep track of which nodes to explore. As long as the queue has nodes, the algorithm dequeues the front node and checks its adjacent unvisited nodes. Each adjacent node that hasn’t been visited gets marked and enqueued.
- This process ensures that the exploration is systematic. BFS is especially helpful for finding the shortest path in unweighted graphs because it looks at all nodes at the current depth before moving on to the next level. This layer-by-layer exploration makes BFS useful for many applications in computer science.
- Start from the source node.
- Visit and mark it as visited.
- For each adjacent unvisited node, recursively perform DFS.
- visited = set()
- def dfs(node):
- if node not in visited:
- visited.add(node)
- for neighbor in graph[node]:
- dfs(neighbor)
- def dfs_iterative(start):
- stack = [start]
- visited = set()
- while stack:
- vertex = stack.pop()
- if vertex not in visited:
- visited.add(vertex)
- stack.extend(graph[vertex])
- Adjacency List: Each node stores a list of adjacent nodes. It is space-efficient for sparse graphs.
- Adjacency Matrix: A 2D array where matrix[i][j] = 1 if there’s an edge from vertex i to j. It is useful for dense graphs but consumes more space.
- graph = {
- ‘A’: [‘B’, ‘C’],
- ‘B’: [‘A’, ‘D’, ‘E’],
- ‘C’: [‘A’, ‘F’],
- ‘D’: [‘B’],
- ‘E’: [‘B’, ‘F’],
- ‘F’: [‘C’, ‘E’]
- }
- Web Crawlers: Use Breadth-First Search (BFS) to systematically visit web pages.
- Social Networks: Find friends of friends using BFS or Depth-First Search (DFS).
- GPS and Map Services: Find shortest routes using BFS.
- Cycle Detection: DFS is used to check for cycles in directed and undirected graphs.
- Topological Sorting: DFS helps in ordering vertices in a Directed Acyclic Graph (DAG).
- AI and Games: DFS helps in exploring game states or solving puzzles.
- Undirected Graphs: Edges are bidirectional; traversal is simpler and commonly used in social networks and basic pathfinding.
- Directed Graphs: Edges have direction; traversal requires careful tracking to avoid infinite loops and to handle asymmetrical connections.
- Large Graphs: Traversal can be computationally intensive.
- Disconnected Graphs: May require multiple traversal attempts to cover all components.
- Cycles: Can lead to infinite loops if not properly handled.
- Memory Constraints: Recursive DFS may fail on deep or infinite graphs due to stack overflow.
- Choosing the Right Traversal: Selecting BFS or DFS depends on the problem (e.g., shortest path vs exhaustive exploration).
Would You Like to Know More About Web Developer? Sign Up For Our Web Developer Courses Now!
Depth-First Search (DFS)
Depth-First Search explores as far along a branch as possible before backtracking. It uses a stack (or recursion) to keep track of the nodes. DFS starts at the root node and explores each branch completely before moving on to the next one. To complement this traversal strategy with language-level performance insights, exploring Go vs Python reveals how Go’s compiled efficiency and concurrency model outperform Python’s interpreted flexibility in scenarios requiring fast execution and deep recursive logic making language choice critical for algorithm-heavy applications.
Steps for DFS:
DFS is useful for scenarios like maze solving, topological sorting, and cycle detection.
Differences Between BFS and DFS
While both BFS and DFS are used for graph traversal, they differ significantly:
| Feature | BFS | DFS |
|---|---|---|
| Data Structure | Queue | Stack/Recursion |
| Approach | Level-wise traversal | Depth-wise traversal |
| Memory Usage | High (due to queue) | Lower (due to recursion) |
| Application | Shortest path in unweighted graph | Cycle detection, topological sort |
| Complexity | O(V+E) | O(V+E) |
BFS explores all neighbors level by level using a queue, while DFS dives deep into each branch using a stack or recursion. To complement these traversal strategies with web service communication models, exploring Soap vs Rest reveals how SOAP’s protocol-driven structure contrasts with REST’s lightweight architecture each suited for different performance, flexibility, and integration needs in distributed systems.
Are You Interested in Learning More About Web Developer? Sign Up For Our Web Developer Courses Today!
Recursive vs Iterative Implementations
DFS can be implemented both recursively and iteratively. The recursive approach is more elegant and easier to implement, but it may lead to a stack overflow for large graphs. The iterative approach uses an explicit stack, giving more control and avoiding recursion depth issues. BFS is inherently iterative and uses a queue, which makes its implementation straightforward. To complement these traversal techniques with efficient development tools, exploring Python IDEs and Code Editors reveals how the right environment featuring syntax highlighting, debugging support, and integrated execution can streamline algorithm implementation and enhance productivity across graph-based applications.
Recursive DFS:
Iterative DFS:
Graph Representation (Adjacency List/Matrix)
Graphs can be represented in two major formats: adjacency matrices and adjacency lists. Each format offers trade-offs in terms of memory usage and traversal efficiency. To complement this foundational understanding of graph representation with practical development skills, exploring Web Developer Training reveals how mastering technologies like JavaScript, React, and backend frameworks enables professionals to build interactive web applications often incorporating graph-based logic for routing, data visualization, and relationship mapping.
Example Adjacency List:
Applications of Graph Traversal
Graph traversal techniques are widely used in various real-world applications: from route optimization and social network analysis to recommendation systems and dependency resolution. To complement these algorithmic strategies with efficient programming capabilities, exploring Go Programming Language reveals how Go’s concurrency model, static typing, and minimal syntax empower developers to implement scalable traversal logic making it ideal for performance-critical systems and distributed computing environments.
Directed vs Undirected Graphs
Traversal strategies work on both directed and undirected graphs, but their implications differ: directed graphs require careful attention to edge direction, while undirected graphs allow bidirectional movement. To complement these algorithmic distinctions with deeper programming control, exploring Python Scopes and Their Built-in Functions reveals how scope types global, local, enclosing, and built-in govern variable accessibility, while built-in functions like `globals()`, `locals()`, and `vars()` provide dynamic insights into namespace behavior during traversal logic and beyond.
Example: Cycle detection in directed graphs often uses a color-coding technique during Depth-First Search (DFS) to differentiate visiting and visited nodes.
Graph Traversal Challenges
Despite their effectiveness, graph traversals come with challenges:
Summary
Graph traversal is a fundamental concept in data structures and algorithms, critical for navigating and processing graph-based data. With Breadth-First Search and Depth-First Search as the primary traversal strategies, developers can address a wide array of computational problems. To complement these algorithmic foundations with practical development skills, exploring Web Developer Training reveals how mastering technologies like JavaScript, React, and backend frameworks enables professionals to build efficient, data-driven web applications often incorporating traversal logic for tasks like DOM manipulation, routing, and state management. Understanding the nuances of each method, their implementations, and the types of graphs they best operate on empowers developers to design efficient solutions. Whether it’s detecting a cycle, finding the shortest path, or exploring social connections, mastering graph traversal is a valuable skill in modern computing.





