Selection Sort Algorithm in Data Structures with Examples

How to Selection Sort Algorithm Works

Let’s consider an array of size n. Here’s how selection sort progresses: To complement such step-by-step algorithmic understanding with practical development expertise, exploring Web Developer Training equips learners with the skills to build structured, efficient web applications covering HTML, CSS, JavaScript, and backend technologies that reinforce logical thinking and real-world implementation.

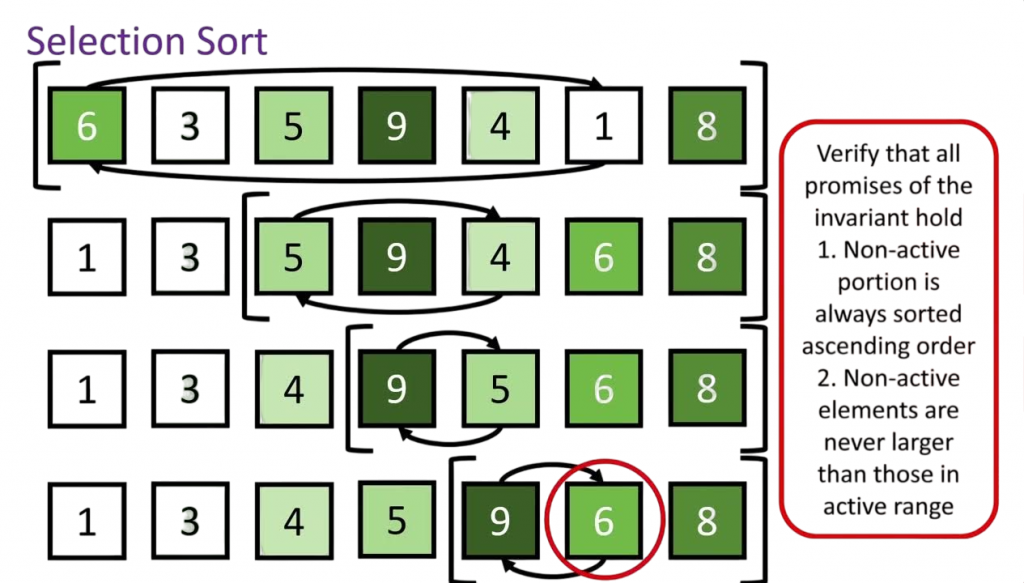
• Step 1: Start with the first element. Find the smallest element in the array and swap it with the first element.
• Step 2: Move to the second element. Again, find the smallest element in the unsorted part (excluding the first element now) and swap it with the second element.
• Step 3: Repeat this process for all positions until the array is sorted.



Would You Like to Know More About Web Developer? Sign Up For Our Web Developer Courses Now!




Visual Example:

Given the array: [29, 10, 14, 37, 13]

• First Pass: Find the minimum (10), swap with 29 → [10, 29, 14, 37, 13]
• Second Pass: Find the next minimum (13), swap with 29 → [10, 13, 14, 37, 29]
• Third Pass: Minimum is already at correct position → [10, 13, 14, 37, 29]
• Fourth Pass: Find min (29), swap with 37 → [10, 13, 14, 29, 37]
• Sorted Array: [10, 13, 14, 29, 37]



Develop Your Skills with Web Developer Certification Course

Weekday / Weekend BatchesSee Batch Details

Pseudocode for Selection Sort

Here is a simple pseudocode for the selection sort algorithm:

• procedure selectionSort(array A):
• n = length(A)
• for i = 0 to n – 1:
• minIndex = i
• for j = i + 1 to n:
• if A[j] < A[minIndex]:
• minIndex = j
• swap A[i] with A[minIndex]

The algorithm keeps selecting the minimum value from the unsorted part and placing it at the beginning of that part, growing the sorted region by one on each iteration.




Are You Interested in Learning More About Web Developer? Sign Up For Our Web Developer Courses Today!




Selection Sort with Example (Dry Run)

Let’s do a dry run with an array: [64, 25, 12, 22, 11]

• i = 0 → Find minimum between indices 0-4 → min = 11 Swap 64 and 11 → [11, 25, 12, 22, 64]
• i = 1 → Find min between 1-4 → min = 12 Swap 25 and 12 → [11, 12, 25, 22, 64]
• i = 2 → Find min between 2-4 → min = 22 Swap 25 and 22 → [11, 12, 22, 25, 64]
• i = 3 → Already in order → [11, 12, 22, 25, 64]
• i = 4 → Sorted.

Web Development Sample Resumes! Download & Edit, Get Noticed by Top Employers! Download

Implementation in C, C++, Java, and Python

C

• void selectionSort(int arr[], int n) {
• for (int i = 0; i < n – 1; i++) {
• int min_idx = i;
• for (int j = i + 1; j < n; j++)
• if (arr[j] < arr[min_idx])
• min_idx = j;
• int temp = arr[min_idx];
• arr[min_idx] = arr[i];
• arr[i] = temp;
• }
• }

C++

• void selectionSort(vector<int>& arr) {
• int n = arr.size();
• for (int i = 0; i < n – 1; i++) {
• int min_idx = i;
• for (int j = i + 1; j < n; j++)
• if (arr[j] < arr[min_idx])
• min_idx = j;
• swap(arr[i], arr[min_idx]);
• }
• }

Java

• void selectionSort(int[] arr) {
• int n = arr.length;
• for (int i = 0; i < n – 1; i++) {
• int min_idx = i;
• for (int j = i + 1; j < n; j++)
• if (arr[j] < arr[min_idx])
• min_idx = j;
• int temp = arr[min_idx];
• arr[min_idx] = arr[i];
• arr[i] = temp;
• }
• }

Python

• def selection_sort(arr):
• n = len(arr)
• for i in range(n):
• min_idx = i
• for j in range(i + 1, n):
• if arr[j] < arr[min_idx]:
• min_idx = j
• arr[i], arr[min_idx] = arr[min_idx], arr[i]

Time & Space Complexity Analysis

Time complexity

• Best Case O(n²): Even if the array is already sorted, selection sort still compares every pair.
• Worst Case O(n²): In the worst case, we still perform n*(n-1)/2 comparisons.
• Average Case O(n²): The time complexity remains quadratic regardless of input order. Selection sort always performs the same number of comparisons, but the number of swaps is minimized compared to bubble sort.

Space complexity

Selection sort has a space complexity of O(1) because it is an in-place sorting algorithm. It doesn’t require any extra memory for sorting, it modifies the original array. It performs O(n) swaps at most, which is better than Bubble Sort that can make up to O(n²) swaps.




Comparison with Other Sorting Algorithms

Algorithm	Time Complexity	Space Complexity	Stability	In-place
Selection Sort	O(n²)	O(1)	No	Yes
Bubble Sort	O(n²)	O(1)	Yes	Yes
Insertion Sort	O(n²)	O(1)	Yes	Yes
Merge Sort	O(n log n)	O(n)	Yes	No
Quick Sort	O(n log n) avg	O(log n)	No	Yes

Key Differences:

• Bubble Sort does more swaps but is stable.
• Insertion Sort is faster on nearly sorted data and stable.
• Merge Sort is faster but requires extra space.
• Quick Sort is faster on average but not stable.




Advantages and Disadvantages of Selection Sort

Advantages:

• Simple to understand and implement.
• Requires no additional memory.
• Performs well on small datasets.
• Less number of swaps compared to bubble sort.

Disadvantages:

• Inefficient on large lists.
• Time complexity is always O(n²), even if the list is already sorted.
• Not a stable sort relative order of equal elements may be changed.




Use Cases and Practical Applications

While not suitable for large datasets, selection sort is useful in:

• Embedded systems with very limited memory where simplicity is valued.
• Teaching basic algorithm design due to its simplicity and step-by-step logic.
• Datasets with costly write operations, as it minimizes the number of swaps.

It’s rarely used in production environments, but useful for understanding algorithm behavior and trade-offs.




Summary

Selection Sort is a simple sorting algorithm. It finds the smallest element from an unsorted list and swaps it with the first element. It has a time complexity of O(n²) and uses O(1) space. This makes it less efficient for large lists. One of its main features is that it is not a stable sorting method, which means it can change the order of equal elements. Even though it is not efficient for big datasets, Selection Sort is easy to implement and understand. To complement such foundational algorithmic knowledge with practical development skills, exploring Web Developer Training equips learners with hands-on experience in building responsive websites and full-stack applications covering HTML, CSS, JavaScript, and backend technologies aligned with industry standards. This makes it a good option for small datasets or teaching.