Last updated on 09th Sep 2025| 10317
(5.0) | 32961 Ratings
E-mail this post
- What is Tree Height?
- Binary Tree Recap
- Recursive Method to Calculate Height
- Iterative Approach Using Queue
- Edge Cases (Skewed Trees)
- Balanced vs Unbalanced Trees
- Code Implementation (C++/Python)
- Tree Height vs Depth
- Time and Space Complexity
- Practice Examples
- Conclusion
What is Tree Height?
Understanding the height of a tree is crucial in computer science, especially when dealing with data structures like binary trees, binary search trees, AVL trees, and heaps. It plays a central role in evaluating the efficiency of operations such as insertion, deletion, and search. To build well-rounded development expertise, pairing algorithmic knowledge with Web Designing Training can help developers create intuitive interfaces that reflect efficient backend logic. The height of a tree is defined as the number of edges on the longest path from the root node to a leaf node. Some definitions use the number of nodes, but the most common definition (used in most textbooks and interviews) is based on edges.
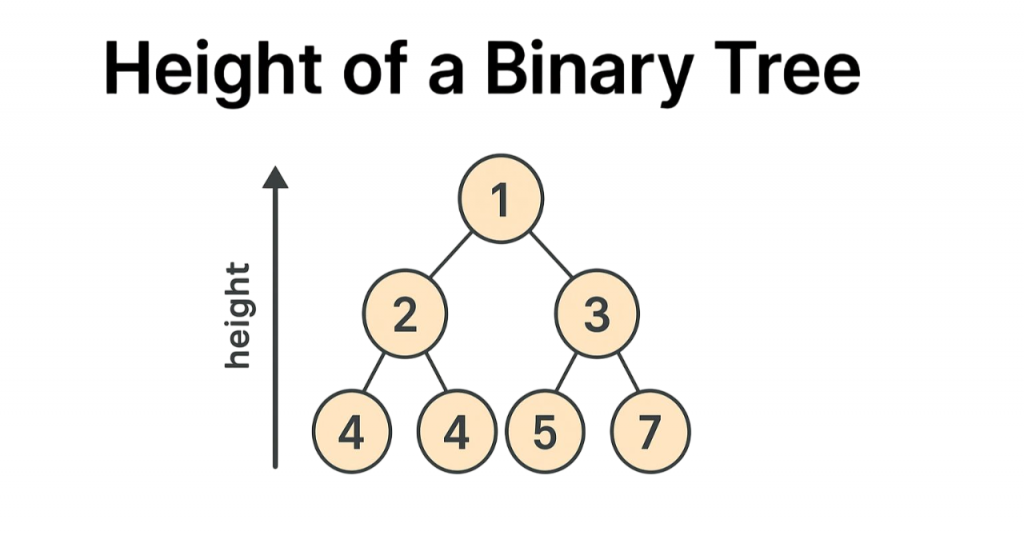
Formal Definition of Tree Height:
- Height of an empty tree = -1 or 0 (depending on convention)
- Height of a leaf node = 0 (no edges below)
- Height of a tree with one node = 0
To Earn Your Web Developer Certification, Gain Insights From Leading Data Science Experts And Advance Your Career With ACTE’s Web Developer Courses Today!
Binary Tree Recap
A binary tree is a hierarchical structure where each node has at most two children, commonly referred to as the left and right child. To translate such foundational knowledge into career growth, exploring Skills that Boosts Java Developer Salaries can help developers align their technical expertise with industry demands and maximize earning potential.
Common Binary Tree Types:
- Full Binary Tree: Every node has 0 or 2 children.
- Complete Binary Tree: All levels are fully filled except possibly the last.
- Perfect Binary Tree: All internal nodes have two children, and all leaves are at the same level.
- Skewed Binary Tree: Nodes are linked in a single line (left-skewed or right-skewed).
Understanding binary trees is essential before diving into height calculations.
Recursive Method to Calculate Height
One of the most intuitive ways to calculate the height of a binary tree is using recursion. To apply such foundational concepts in real-world scenarios, exploring Python Project Ideas for Beginners can help you build hands-on experience through structured challenges that reinforce core programming techniques.
Logic:
- Recursively compute the height of left and right subtrees.
- Height of current node = 1 + max(leftHeight, rightHeight)
Python Example:
- def height(root):
- if not root:
- return -1
- return 1 + max(height(root.left), height(root.right))
C++ Example:
- int height(TreeNode* root) {
- if (root == NULL)
- return -1;
- return 1 + max(height(root->left), height(root->right));
- }
This divide-and-conquer approach is clean and readable but can have performance issues on highly unbalanced trees.
Iterative Approach Using Queue
Instead of recursion, we can use level order traversal (Breadth-First Search) to compute height. To round out your technical expertise, combining algorithmic strategies with Web Designing Training can help you build visually structured interfaces that reflect logical depth and enhance user engagement.
Logic to Calculate Tree Height Using Level Order Traversal:
- Use a queue and count the number of levels.
- Each level processed increases the height count.
Python Example:
- from collections import deque
- def height_iterative(root):
- if not root:
- return -1
- q = deque([root])
- height = -1
- while q:
- for _ in range(len(q)):
- node = q.popleft()
- if node.left:
- q.append(node.left)
- if node.right:
- q.append(node.right)
- height += 1
- return height
This approach is more memory-efficient and stack-safe than recursion.
Would You Like to Know More About Web Developer? Sign Up For Our Web Developer Courses Now!
Edge Cases (Skewed Trees)
Skewed trees are trees where all nodes are either on the left or right side, forming a straight line. To experiment with such structures in code, understanding How to Run Python Scripts is essential, as it enables you to execute and test recursive tree logic efficiently using Python’s interactive shell or command-line tools.
Example
- Left Skewed: 1 → 2 → 3 → 4 → 5
- Right Skewed: 1 ← 2 ← 3 ← 4 ← 5
- Height = n−1n – 1, where nn is the number of nodes
Such trees behave like linked lists and are the worst case for many tree operations.
Develop Your Skills with Web Developer Certification Course
Weekday / Weekend BatchesSee Batch DetailsBalanced vs Unbalanced Trees
Balanced Tree:
- The height difference between left and right subtrees is at most 1 for all nodes.
- Ensures better performance for search and insertion.
- Examples: AVL Tree, Red-Black Tree
Unbalanced Tree:
- Large height difference between branches.
- Degrades performance to linear time.
Height helps determine if a tree is balanced.
- def is_balanced(root):
- if not root:
- return True, -1
- left_balanced, left_height = is_balanced(root.left)
- right_balanced, right_height = is_balanced(root.right)
- balanced = left_balanced and right_balanced and abs(left_height – right_height) <= 1
- return balanced, 1 + max(left_height, right_height)
Are You Interested in Learning More About Web Developer? Sign Up For Our Web Developer Courses Today!
Code Implementation (C++/Python)
Python (Recursive):
- class Node:
- def __init__(self, key):
- self.data = key
- self.left = self.right = None
- def height(root):
- if root is None:
- return -1
- return 1 + max(height(root.left), height(root.right))
C++ (Recursive):
- struct Node {
- int data;
- Node* left;
- Node* right;
- };
- int height(Node* root) {
- if (root == NULL)
- return -1;
- return 1 + max(height(root->left), height(root->right));
- }
Both versions return the height in terms of edges.
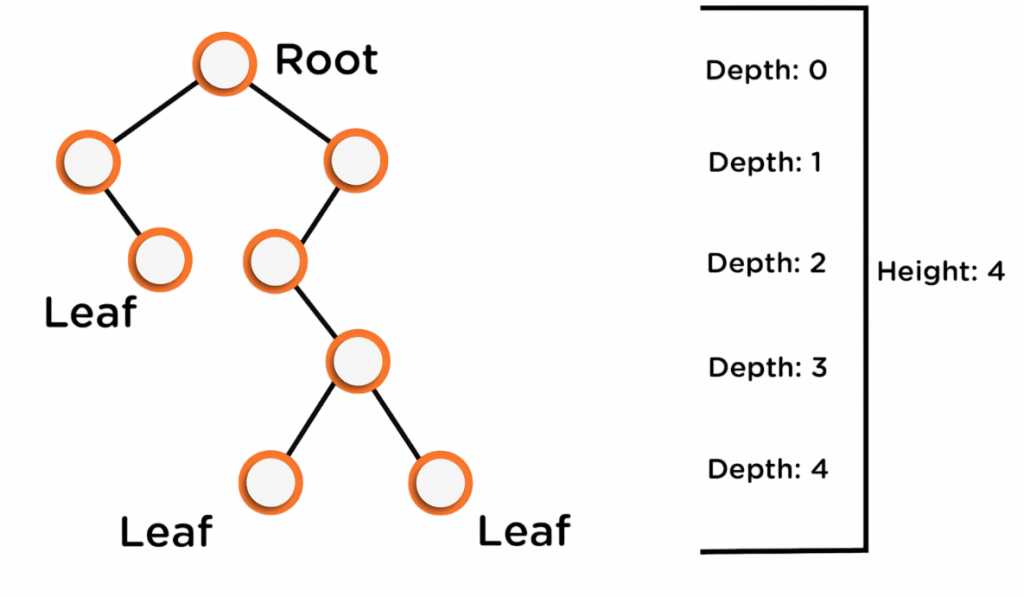
Tree Height vs Depth
In a tree data structure, two important concepts to understand are height and depth. The height of a tree is the distance from a selected node to its furthest leaf, measured in edges. For the entire tree, the height is usually calculated from the root node, which makes it a key feature of its structure. Essentially, the height shows how many levels exist below the root down to the leaves. In contrast, depth measures how far down a specific node is from the root. The depth of the root is zero, and as you go further down the tree, the depth increases. Understanding both height and depth can help analyze tree algorithms, improve operations, and manage hierarchical data more effectively. By grasping these differences, one can better appreciate the dynamics of tree structures in computer science and related fields.
Time and Space Complexity
When implementing tree traversal methods, two common approaches are recursive and iterative methods. Each approach has its own advantages and considerations. The recursive method operates with a time complexity of O(n), as each node is visited once, making it efficient for balanced trees. However, its space complexity is O(h), where ‘h’ represents the height of the tree, because of the call stack used during recursion. In contrast, the iterative method, often carried out using breadth-first search (BFS), also has a time complexity of O(n). However, its space complexity is larger at O(n) because it uses a queue for level order traversal. While recursion can be simple and effective for balanced trees, it can create issues in deeply skewed trees, where the call stack could lead to a stack overflow. Therefore, for extremely unbalanced trees, using an iterative approach is safer and more reliable to avoid these problems. Understanding these differences can help you choose the most suitable traversal method based on the specific traits of the tree you are working with.
Practice Examples
- Balanced Tree Check: Write a function to check if a binary tree is height-balanced.
- Maximum Depth of Binary Tree: Compute the deepest level of the tree.
- Skewed Tree Height Analysis: Build a skewed tree and compute its height.
- Height Using DFS and BFS: Implement both approaches and compare on various inputs.
Conclusion
The height of a tree is a foundational concept that influences almost every operation in tree data structures. Whether you’re optimizing performance, balancing trees, or analyzing complexity, understanding height is key. Using both recursive and iterative methods, you can accurately compute and analyze tree height across various scenarios. To complement algorithmic depth with front-end development skills, Web Designing Training offers practical insights into layout design, styling, and building user-friendly interfaces that visualize complex logic effectively. Mastering this concept prepares you for advanced topics like AVL trees, heaps, red-black trees, and even file system design.
