Last updated on 09th Sep 2025| 10350
(5.0) | 32961 Ratings
E-mail this post
- What is Matrix Multiplication?
- Matrix Multiplication Rules
- Input Matrix Dimensions
- Initializing Matrices in C
- Writing the Core Logic
- Using Nested Loops
- Displaying Output Matrix
- Conclusion
What is Matrix Multiplication?
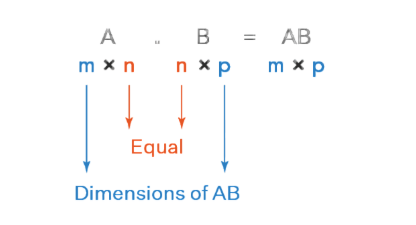
In linear algebra, matrix multiplication is a basic operation that involves calculating a new matrix from two given matrices. This idea is especially crucial to C programming in fields like data analysis, scientific computing, simulations, and graphics processing. To put it simply, matrix multiplication computes each element of the result matrix by taking the dot product of the rows in the first matrix with the columns in the second matrix. The product C = A × B is a m x p matrix if A is a m x n matrix and B is a n x p matrix. In contrast to addition or subtraction, matrix multiplication is not element-wise and has certain guidelines that must be adhered to in order to function properly. In linear algebra, matrix multiplication is a basic operation that creates a third matrix by combining two matrices. Only when the number of rows in the second matrix equals the number of columns in the first matrix is it defined. Their product, AB, will be a matrix of size m × p if matrix A is m × n and matrix B is n × p. The dot product of a row in the first matrix and a column in the second is used to calculate each element in the final matrix. This entails adding together the results of multiplying corresponding elements. The dot product of a row in the first matrix and a column in the second is used to calculate each element in the final matrix. This entails adding together the results of multiplying corresponding elements. The product of the items in the first row of A and the first column of B, for instance, is the element in the product’s first row and first column. Since matrix multiplication is not commutative, AB and BA are not always equal. It is distributive and associative over addition, though. Computer graphics, physics simulations, machine learning, and linear equation systems all make extensive use of matrix multiplication. Data transformation and representation in several dimensions are made possible by it.
To Earn Your Web Developer Certification, Gain Insights From Leading Data Science Experts And Advance Your Career With ACTE’s Web Developer Courses Today!
Matrix Multiplication Rules
Matrix multiplication adheres to several mathematical rules:
- Dimensional Compatibility: For two matrices A and B to be multiplied, the number of columns in A must be equal to the number of rows in B. If A is of order m x n and B is of order n x p, the resulting matrix C will be of order m x p.
- Non-Commutativity: Matrix multiplication is not commutative, i.e., A × B ≠ B × A in general.
- Associativity: It is associative: (A × B) × C = A × (B × C).
- Distributivity: Matrix multiplication distributes over addition: A × (B + C) = A × B + A × C.
- Scalar Multiplication Compatibility: Scalars can be multiplied with matrices either before or after the matrix multiplication:
- Enter rows and columns for first matrix: 2 3
- Enter rows and columns for second matrix: 3 2
- The resultant matrix will then be of dimension 2 x 2.
- for (i = 0; i < rowsA; i++) {
- for (j = 0; j < colsB; j++) {
- C[i][j] = 0;
- for (k = 0; k < colsA; k++) {
- C[i][j] += A[i][k] * B[k][j];
- }
- }
- }
- Outer loop iterates over rows of A.
- Middle loop iterates over columns of B.
- The inner loop performs the dot product.
- for (i = 0; i < rowsA; i++) {
- for (j = 0; j < colsB; j++) {
- printf(“%d “, C[i][j]);
- }
- printf(“\n”);
- }
k × (A × B) = (kA) × B = A × (kB).
Understanding these rules ensures accurate implementation in C programs.
Input Matrix Dimensions
Before performing multiplication, it is essential to input the correct dimensions of both matrices. If matrix A has dimensions a x b and matrix B has Input Matrix Dimensions c x d, then b must equal c for the multiplication to proceed.The dimensions of the matrices must match in order to accomplish matrix multiplication: the first matrix’s number of columns must equal the second matrix’s number of rows. The matrices can be multiplied if the first matrix, Matrix A, has dimensions of m × n (m rows and n columns), while the second matrix, Matrix B, has dimensions of n × p (n rows and p columns). A new matrix with dimensions m × p will be the outcome of this multiplication.
Sample Input Flow:
This check should be implemented in the code to avoid runtime errors and invalid operations.
Would You Like to Know More About Web Developer? Sign Up For Our Web Developer Courses Now!
Initializing Matrices in C
Matrices in C are typically implemented as 2D arrays. Here’s how you can declare and initialize them:
int A[10][10], B[10][10], C[10][10];
If dynamic memory allocation is needed for large matrices, malloc() or calloc() can be used with pointers.
Example static initialization:int A[2][3] = {{1, 2, 3}, {4, 5, 6}};
int B[3][2] = {{1, 2}, {3, 4}, {5, 6}};
Proper initialization avoids garbage values and ensures clean calculations.
Develop Your Skills with Web Developer Certification Course
Weekday / Weekend BatchesSee Batch DetailsWriting the Core Logic
The core logic of matrix multiplication involves calculating the sum of the products of corresponding elements from the row of matrix A and the column of matrix B.The core logic of matrix multiplication involves calculating each element of the resulting matrix by taking the dot product of corresponding rows from the first matrix and columns from the second matrix. For every element in the product matrix, you select a row from the first matrix and a column from the second matrix. Then, multiply the elements pairwise and sum all these products to get a single value for that position in the result matrix. This process is repeated for every row of the first matrix and every column of the second matrix until the entire resulting matrix is filled. This method works because each element in the output matrix represents how much the row from the first matrix aligns or interacts with the column from the second matrix, making it a powerful tool for transformations and combining data across dimensions.
Formula:For each element in result matrix C[i][j]:
C[i][j] = A[i][0] * B[0][j] + A[i][1] * B[1][j] + … + A[i][n-1] * B[n-1][j];
This computation is done through nested loops, iterating over rows of A and columns of B.
Are You Interested in Learning More About Web Developer? Sign Up For Our Web Developer Courses Today!
Using Nested Loops
Using nested loops for matrix multiplication entails iterating through each component of the resultant matrix and gradually calculating its value. Three nested loops are typically used: the innermost loop multiplies related elements of the row and column and adds them up, the middle loop goes through each column of the second matrix, Input Matrix , and the outside loop goes through each row of the first matrix. In particular, the innermost loop multiplies elements from the current row of the first matrix and the current column of the second matrix for each place in the output matrix, adding up the total to create the final value. A three-level nested loop is commonly used for matrices .
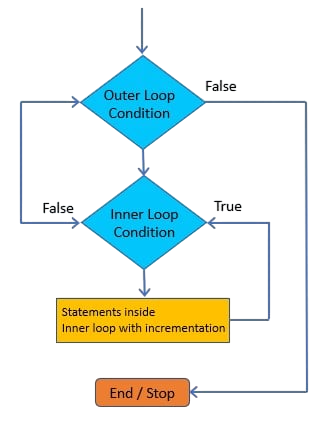
multiplication in C:
Explanation:
This approach is efficient and easy to understand for beginners.
Displaying Output Matrix
Displaying output matrix involves presenting the result of the matrix multiplication in a clear, organized format. After computing all the elements of the product matrix, you typically print or show the matrix row by row, with each element separated by spaces or tabs. This helps visualize the structure of the matrix, making it easier to understand the dimensions and values. Displaying the matrix in a grid-like format allows you to quickly verify the results, compare values, and use the output in further calculations or applications. In programming, this often means using loops to iterate through each row and column of the resulting matrix and printing the elements in a neat, readable way. Clear presentation of the output matrix is essential for debugging and interpreting the results of matrix multiplication effectively. To display the result, loop through each element of the result matrix and print it:
Clear formatting improves readability of output matrices, especially for larger sizes.
Conclusion
To sum up, matrix multiplication is a basic linear algebraic operation that computes the dot products of rows and columns to create a new matrix from two matrices. To carry out this operation successfully, one must comprehend the dimension requirements as well as the fundamental reasoning underlying the multiplication process. A simple method for implementing matrix multiplication in programming is to use nested loops, which enable the methodical computation of each element in the resultant matrix. Last but not least, showing the output matrix clearly guarantees that the results are simple to understand and validate. Gaining proficiency in matrix multiplication paves the way for several real-world uses in domains including scientific computing, machine learning, and computer graphics.
