Minimum Spanning Tree: Understand Kruskal & Prim Algorithms

Introduction to MST

Graphs are fundamental to computer science, and among the many problems on graphs, finding a Minimum Spanning Tree (MST) is one of the most important. MSTs help reduce redundancy and cost in connected networks while preserving connectivity. From designing computer networks to road maps and electrical circuits, MST algorithms provide efficient solutions. To expand your skillset beyond algorithms, Web Designing Training can equip you with the tools to build intuitive interfaces that visualize complex systems and enhance user interaction. A spanning tree of a graph is a subgraph that connects all vertices together without any cycles and uses the minimum number of edges (n-1 for a graph with n nodes). A Minimum Spanning Tree (MST) is a spanning tree whose total edge weight is the minimum among all possible spanning trees.

Key Characteristics of Minimum Spanning Trees (MST):

• Spanning all vertices
• No cycles
• Exactly V − 1 edges (for V vertices)
• Minimum total weight

To Earn Your Web Developer Certification, Gain Insights From Leading Data Science Experts And Advance Your Career With ACTE’s Web Developer Courses Today!

Applications of MST

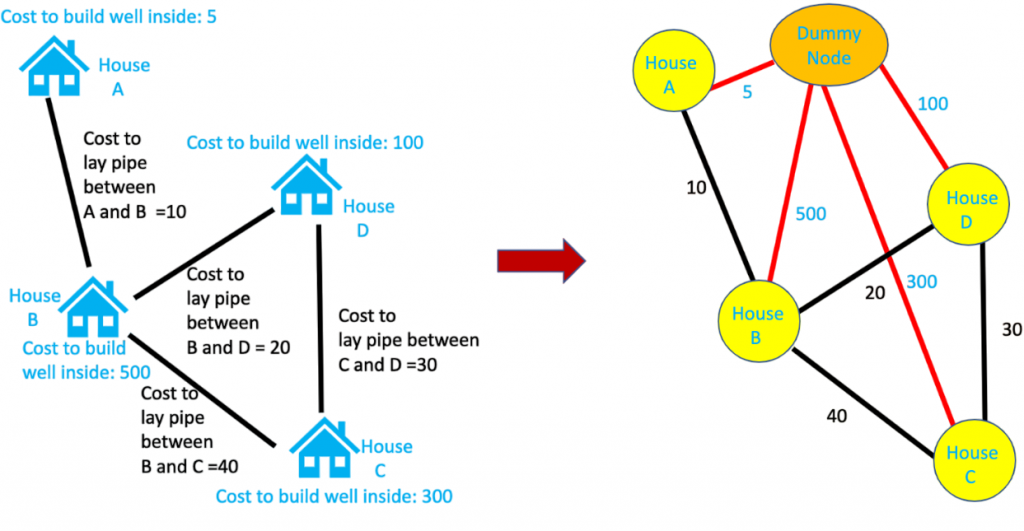
MSTs are widely used in various real-world and theoretical applications:

• Network Design: Constructing cost-effective communication, electrical, or transportation networks.
• Approximation Algorithms: Applied in problems like the Traveling Salesman Problem (TSP).
• Image Segmentation: Used in computer vision to cluster pixels effectively.
• Cluster Analysis: Grouping data in unsupervised learning tasks.
• Urban Planning: Designing roads, water distribution, and wiring with minimal cost.

The universal nature of MST problems makes them indispensable in fields like operations research, AI, and networking.

Graph Terminology Recap

Before diving into MST algorithms, it’s essential to review some key graph terminology concepts:

• Vertex (Node): A point in the graph.
• Edge: A connection between two vertices.
• Weight: Cost or distance assigned to an edge.
• Undirected Graph: Edges have no direction.
• Connected Graph: There is a path between every pair of vertices.
• Cycle: A path that starts and ends at the same vertex without retracing steps.

MST algorithms are designed for connected, undirected, weighted graphs.

Subscribe To Contact Course Advisor

Subscribe

Kruskal’s Algorithm

Kruskal’s algorithm is an efficient greedy method for finding a Minimum Spanning Tree (MST) in a graph. It works especially well with sparse graphs. The process starts by sorting all the edges in ascending order by their weights. After sorting, an empty MST is created. While mastering algorithms like MST is essential, complementing your skillset with Web Designing Training can help you build visually intuitive interfaces that present complex logic in user-friendly formats. 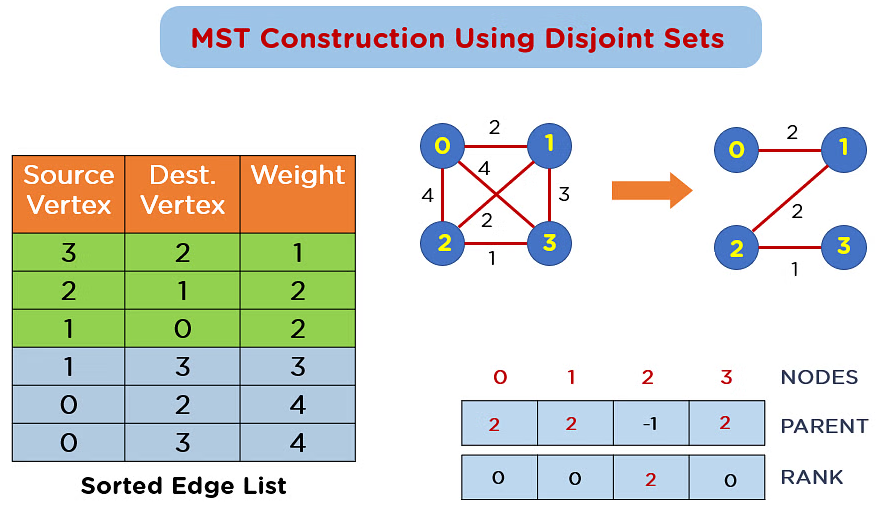The algorithm then goes through each edge in this sorted list and checks if adding that edge would create a cycle, using the Union-Find data structure for this check. If adding the edge does not create a cycle, it gets included in the MST. This continues until the MST contains exactly V-1 edges, where V is the number of vertices in the graph. Kruskal’s algorithm is known for its simplicity and efficiency, making it a popular choice in network design and graph theory.

Would You Like to Know More About Web Developer? Sign Up For Our Web Developer Courses Now!

Prim’s Algorithm

Prim’s Algorithm is a well-known method for finding the Minimum Spanning Tree (MST) of a graph. It begins with any vertex and gradually builds the MST by adding one vertex at a time. The main steps involve keeping a list of edges that connect the current MST to the other vertices. At each step, the algorithm picks the edge with the smallest weight that connects the MST to a new vertex, thus expanding the tree. This process continues until all vertices are part of the MST. One of the main benefits of Prim’s Algorithm is its efficiency, especially with dense graphs. By using a priority queue, or min-heap, it can quickly find the minimum-weight edges needed to expand the MST. This mix of simplicity and effectiveness makes Prim’s Algorithm a popular choice for solving graph-related problems in various applications.

Develop Your Skills with Web Developer Certification Course

Weekday / Weekend BatchesSee Batch Details

Union-Find in Kruskal

To avoid cycles in Kruskal’s algorithm, we use the Union-Find (Disjoint Set) data structure:

• Find(): Determines which set a vertex belongs to.
• Union(): Merges two sets if they are disjoint.

With path compression and union by rank, Union-Find ensures efficient edge inclusion checks in nearly O(1) time.

Example:

• int find(int parent[], int i) {
• if (parent[i] != i)
• parent[i] = find(parent, parent[i]);
• return parent[i];
• }
• void unionSets(int parent[], int x, int y) {
• int xroot = find(parent, x);
• int yroot = find(parent, y);
• parent[xroot] = yroot;
• }

Are You Interested in Learning More About Web Developer? Sign Up For Our Web Developer Courses Today!

Priority Queue in Prim

Prim’s algorithm can be optimized using a min-priority queue (heap) to efficiently pick the smallest edge at every step.

Benefits of Optimized Graph Algorithms:

• Reduces time from O(V²) to O(E log V)
• Especially helpful in graphs with large numbers of vertices and edges

Data Structures Used:

• Heap / Min-Heap
• Visited array
• Adjacency list for graph representation

Web Development Sample Resumes! Download & Edit, Get Noticed by Top Employers! Download

Sample MST Code in C++

Kruskal’s Algorithm Example:

• #include <bits/stdc++.h>
• using namespace std;
• struct Edge {
• int u, v, weight;
• };
• bool compare(Edge a, Edge b) {
• return a.weight < b.weight;
• }
• int find(int parent[], int i) {
• if (parent[i] != i)
• parent[i] = find(parent, parent[i]);
• return parent[i];
• }
• void unionSet(int parent[], int x, int y) {
• int xroot = find(parent, x);
• int yroot = find(parent, y);
• parent[xroot] = yroot;
• }
• int main() {
• int V = 4;
• vector<Edge> edges = {
• {0, 1, 10}, {0, 2, 6}, {0, 3, 5}, {1, 3, 15}, {2, 3, 4}
• };
• sort(edges.begin(), edges.end(), compare);
• int parent[V];
• for (int i = 0; i < V; ++i) parent[i] = i;
• vector<Edge> mst;
• for (Edge e : edges) {
• int x = find(parent, e.u);
• int y = find(parent, e.v);
• if (x != y) {
• mst.push_back(e);
• unionSet(parent, x, y);
• }
• }
• cout << “MST edges:\n”;
• for (Edge e : mst)
• cout << e.u << ” – ” << e.v << ” = ” << e.weight << endl;
• return 0;
• }

This builds an MST using Kruskal’s algorithm efficiently.

Practice Problems

Improve your understanding of MSTs by practicing these problems:

• Minimum Spanning Tree
• Network Connection
• Connecting Cities With Minimum Cost
• Prim’s Algorithm
• MST with Negative Edges

Conclusion

The Minimum Spanning Tree is a foundational concept in graph theory and algorithm design. Whether you’re reducing the cost of a network or solving clustering problems, MST algorithms like Kruskal’s and Prim’s provide efficient strategies. With mastery over Union-Find, priority queues, and graph representations, you can apply MSTs in a wide range of real-world and coding interview problems. To broaden your development skillset beyond algorithms, exploring Web Designing Training can help you build visually engaging interfaces and understand layout, styling, and user experience fundamentals. By understanding their logic, time complexity, and application scenarios, you can become proficient in one of the most impactful areas of computer science and competitive programming.