Data Structure Analysis with Asymptotic Notation

Importance in Algorithm Design

• Asymptotic notation plays a vital role by helping us select or design algorithms that perform well with larger datasets. It allows engineers and computer scientists to evaluate different solutions, forecast resource usage, and avoid algorithms that become impractical when input size increases. To complement such analytical precision with clean, readable code, exploring Must-Know Identifiers highlights the rules and best practices for naming variables, functions, and classes in Python ensuring clarity, maintainability, and consistency across complex systems.
• For example, choosing between a bubble sort with O(n2)O(n^2) complexity and a merge sort with O(nlog⁡n)O(n \log n) can make a dramatic difference in performance when sorting millions of elements. Similarly, in competitive programming and technical interviews, asymptotic analysis ensures you can justify your solution’s efficiency. In real-world applications like databases, search engines, or machine learning, it influences architecture decisions and software design.



Would You Like to Know More About Web Developer? Sign Up For Our Web Developer Courses Now!




Big O Notation

The most commonly used asymptotic notation is Big O, which denotes the upper bound of an algorithm’s running time. It describes the worst-case scenario, where the algorithm takes the maximum number of steps relative to the input size nn. To complement such performance analysis with control flow mastery, exploring Break, Continue & Pass Statements in Python reveals how these constructs manage loop execution enabling developers to skip iterations, exit loops early, or insert syntactic placeholders for future logic. For example, an algorithm with time complexity O(n2)O(n^2) means the execution time increases proportionally to the square of the input size. Big O provides a conservative estimate of resource usage, ensuring the algorithm will not exceed the given limit. It is useful for evaluating scalability. Common Big O complexities include:



• O(1): Constant time execution time does not depend on input size.
• O(log n): Logarithmic time performance improves with divide-and-conquer strategies.
• O(n): Linear time time grows proportionally with input size.
• O(n log n): Linearithmic time common in efficient sorting algorithms like mergesort and heapsort.
• O(n²): Quadratic time typical in nested loops, example bubble sort.
• O(2ⁿ): Exponential time grows rapidly, often seen in brute-force recursive solutions.
• O(n!): Factorial time extremely slow, common in exhaustive permutations or traveling salesman problem.

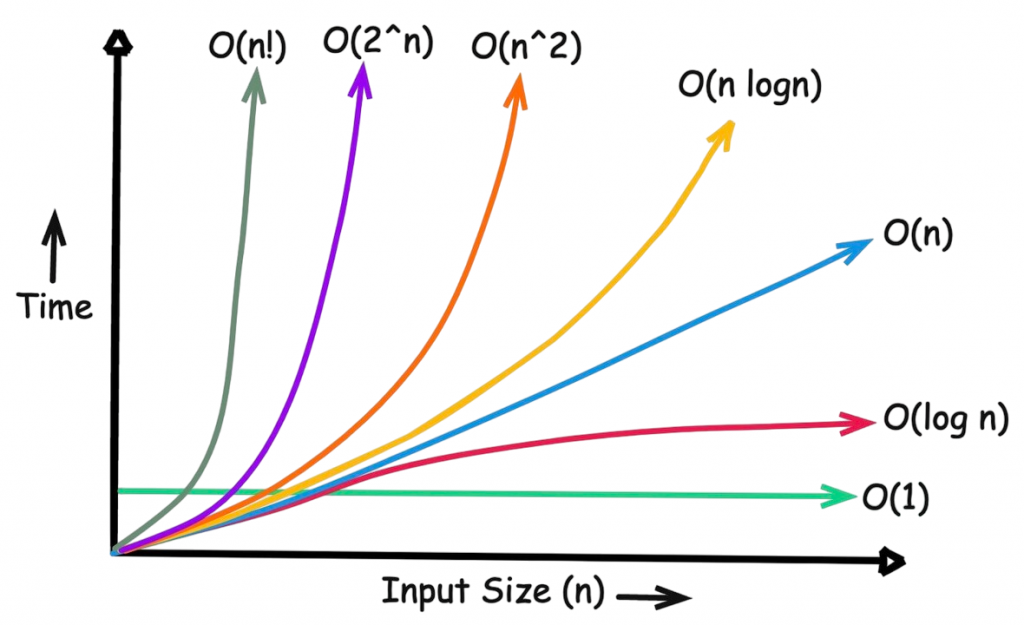
Understanding Big O helps in selecting data structures and algorithms that meet performance requirements.



Develop Your Skills with Web Developer Certification Course

Weekday / Weekend BatchesSee Batch Details

Omega (Ω) and Theta (θ) Notations

While Big O gives an upper bound, Omega(Ω) and Theta(θ) provide additional context. To complement such analytical frameworks with foundational object-oriented principles, exploring Object Class in Java reveals how every class in Java inherits core methods like `toString()`, `hashCode()`, and `equals()` forming the root of the inheritance hierarchy and enabling consistent behavior across all Java objects.



• Omega (Ω) Notation: Denotes the lower bound, representing the best-case scenario of an algorithm. For example, Ω(n) means the algorithm will take at least n steps in the best case. Though not always practically useful alone, it offers insight into the most favorable execution time.
• Theta (θ) Notation: Denotes the tight bound, representing both upper and lower bounds. If an algorithm has a time complexity of Θ(n log n), it means that it always takes time proportional to n log n for large input sizes. Theta is valuable when the best and worst-case complexities converge.

Together, Big O, Omega, and Theta notations provide a complete picture of an algorithm’s behavior across all conditions.




Are You Interested in Learning More About Web Developer? Sign Up For Our Web Developer Courses Today!




Comparing Growth Rates

Growth rate comparison helps determine which algorithm will perform better as input size increases. Even if two algorithms seem equally fast on small inputs, their performance diverges dramatically for large inputs depending on their growth rates. To complement such analytical insights with practical front-end development skills, exploring Web Developer Training equips learners to build responsive, visually compelling websites using HTML, CSS, JavaScript, and modern UI frameworks bridging performance theory with user-focused design.

Let’s consider two algorithms:

• Algorithm A: O(nlog⁡n)O(n \log n).
• Algorithm B: O(n2)O(n^2).

For small nn, say 10 or 20, both might complete in milliseconds. However, as nn reaches 10,000 or more, Algorithm A remains feasible, while Algorithm B becomes significantly slower due to its quadratic growth. This principle underscores the importance of selecting algorithms based on growth rates rather than fixed benchmarks.

Web Development Sample Resumes! Download & Edit, Get Noticed by Top Employers! Download

Best, Worst, and Average Case

Understanding an algorithm’s behavior across different scenarios is essential for robust design. Asymptotic notations help categorize performance as: To complement such analytical depth with structured execution flow, exploring Must-Know Main Function in Python reveals how the `__name__ == “__main__”` construct defines a clear entry point enabling modular design, controlled execution, and better debugging across scripts and imported modules.

• Best Case (Ω): Minimum number of steps needed.
• Worst Case (O): Maximum steps required.
• Average Case (commonly O): Expected number of operations over all possible inputs.

For instance, in linear search:

• Best case: Element is found at the first position → Ω(1)Ω(1).
• Worst case: Element not found or at last position → O(n)O(n).
• Average case: Element somewhere in the middle → O(n/2)O(n/2), simplified to O(n)O(n).

When designing real-time systems or mission-critical software, worst-case analysis is prioritized. For probabilistic or heuristic applications, average-case becomes more relevant.

Graphical Interpretation

Graphing asymptotic notations offers intuitive insights. On a graph where the X-axis represents input size nn and the Y-axis shows the number of operations, each complexity class plots a distinct curve: To complement such performance visualization with object-oriented design principles, exploring Inheritance in Java reveals how classes can extend functionality from parent classes promoting code reuse, modularity, and hierarchical relationships that mirror real-world systems.

• O(1) is a flat line performance that doesn’t depend on input size.
• O(log n) curves gently upward.
• O(n) is a straight diagonal line.
• O(n²) shows a steep upward curve.
• O(2ⁿ) skyrockets rapidly.

Such graphs help visualize scalability. When visualized, it becomes clear how linear and quadratic algorithms diverge as input grows. Tools like matplotlib in Python can help plot these curves for educational purposes.




Common Time Complexities

Here’s a quick look at commonly encountered time complexities and where they appear:

• O(1): Accessing an array element, hash map lookups.
• O(log n): Binary search, heap operations.
• O(n): Traversing a list or array.
• O(n log n): Merge sort, quicksort (average case).
• O(n²): Bubble sort, insertion sort, matrix multiplication (naive).
• O(2ⁿ): Solving problems via recursion (e.g., subsets, traveling salesman).
• O(n!): Brute-force permutation generation.

Understanding these helps in selecting algorithms and identifying inefficiencies in code during optimization.

Space Complexity Notation

In addition to time complexity, space complexity is crucial, especially in memory-limited systems like embedded devices. Space complexity describes how much extra memory an algorithm uses in terms of input size nn For Example:

• Merge sort requires O(n)O(n) extra space.
• Quick sort is O(log⁡n)O(\log n) due to recursive stack calls.
• Algorithms that modify input in-place, like bubble sort, use O(1)O(1) space.

Space complexity is also expressed using Big O, and optimizing for it is important in areas like mobile development, IoT, and large-scale distributed systems.

Choosing Efficient Algorithms

Efficiency is context-dependent. A theoretically faster algorithm may perform worse if input size is small or implementation is complex. For example, insertion sort can outperform merge sort for small arrays due to minimal overhead.

When choosing an algorithm:

• Analyze input size and frequency.
• Consider average vs worst-case.
• Balance between time and space complexity.
• Factor in simplicity and ease of implementation.
• Test real-world performance and edge cases.

In coding interviews, theoretical efficiency and code clarity are both judged. In production, maintainability and real-time responsiveness are prioritized.

Interview-Oriented Questions

Understanding asymptotic notation is essential in technical interviews. Common questions include: To complement such analytical depth with practical string manipulation skills, exploring Python Split Method reveals how to divide strings based on delimiters, control the number of splits, and extract structured data efficiently making it a must-know tool for parsing input and handling textual data in Python.

• Compare the time complexities of different sorting algorithms.
• What is the difference between O(n) and O(log n)?
• Why is Big O used instead of actual runtime?
• How does recursion affect time and space complexity?
• What’s the space complexity of a depth-first search?
• Can two algorithms with the same Big O behave differently?
• How would you optimize an algorithm with O(n²) complexity?

Additionally, candidates are often asked to identify or improve the time complexity of given code snippets. Practicing such problems sharpens both analytical and coding skills.

Conclusion

Asymptotic notation provides a foundational framework for evaluating the efficiency of algorithms and data structures. It abstracts away the machine-specific details and focuses on how the algorithm performs as input size scales. By mastering Big O, Omega, and Theta notations, understanding different growth rates, analyzing best/worst/average cases, and considering both time and space complexity, one can write robust, scalable, and optimal code. To complement such algorithmic efficiency with front-end development skills, exploring Web Developer Training provides hands-on experience in HTML, CSS, JavaScript, and UI/UX design empowering learners to build responsive, visually engaging websites that perform well across devices and user scenarios. From academic theory to real-world applications and coding interviews, asymptotic analysis remains a pillar of computer science.