
- Introduction to Sorting Algorithms
- What is Quick Sort?
- How Quick Sort Works – Step-by-Step
- Choosing a Pivot Element
- Partitioning the Array
- Recursive Implementation of Quick Sort
- Time and Space Complexity Analysis
- Best Case, Worst Case, and Average Case
- Conclusion
Introduction to Sorting Algorithms
Sorting is a fundamental operation in computer science and programming. It involves arranging data in a specific order, typically ascending or descending. Sorting is used in a wide variety of applications such as database indexing, search optimization, and data analysis. Numerous sorting algorithms exist, each with distinct advantages, disadvantages, and use cases. Some of the most common include Bubble Sort, Merge Sort, Insertion Sort, Heap Sort, and Quick Sort. Among these, Quick Sort stands out due to its efficiency and widespread practical use in libraries and systems Web Designing & Development Training. Sorting algorithms are fundamental concepts in computer science and are essential for organizing data efficiently. Sorting refers to the process of arranging elements in a specific order typically in ascending or descending order. This is a common operation used in various applications, such as searching, data analysis, and optimization problems. There are many different sorting algorithms, each with its own approach, efficiency, and use case. Some of the most widely used sorting algorithms include Bubble Sort, Selection Sort, Insertion Sort, Merge Sort, Quick Sort, and Heap Sort. These algorithms vary in terms of time complexity, space usage, stability, and whether they are suitable for large datasets. Understanding sorting algorithms helps build a strong foundation in data structures and algorithms (DSA), especially for those preparing for technical interviews or working with large-scale data processing systems. Efficient sorting can significantly improve the performance of applications, particularly when dealing with large or frequently updated datasets. In this article, we’ll explore one of the most efficient and widely used sorting algorithms: Quick Sort. We’ll look at how it works, how to choose a pivot, how partitioning operates, and analyze its performance in best, worst, and average cases.
To Earn Your Web Developer Certification, Gain Insights From Leading Data Science Experts And Advance Your Career With ACTE’s Web Developer Courses Today!
What is Quick Sort?
Quick Sort is a divide-and-conquer sorting algorithm that works by selecting a “pivot” element from the array and partitioning the remaining elements into two sub-arrays, those less than the pivot and those greater than the pivot. These sub-arrays are then recursively sorted. It is known for its average-case time complexity of O(n log n) and for being an in-place sorting method, meaning it requires only a small, constant amount of additional storage. Developed by Tony Hoare in 1959, Quick Sort remains one of the fastest and most efficient sorting algorithms for average use cases, Polymorphism in C++ and it is widely used in system libraries like Python’s sort() and C’s standard library.Quick Sort is a highly efficient divide-and-conquer sorting algorithm used to sort elements in an array or list. It works by selecting a pivot element from the array and then partitioning the other elements into two sub-arrays, those less than the pivot and those greater than the pivot. This process is applied recursively to the sub-arrays until the entire array is sorted.
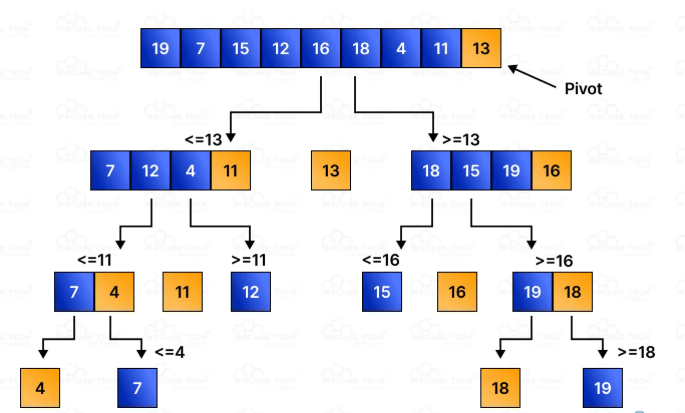
Quick Sort is known for its average-case time complexity of O(n log n), making it faster than simple algorithms like Bubble Sort or Insertion Sort for large datasets. It is also an in-place algorithm, meaning it doesn’t require extra space for sorting, which makes it memory-efficient. Despite its worst-case time complexity being O(n²) (usually when the pivot selection is poor), Quick Sort is often preferred in practice due to its speed and performance on average.
How Quick Sort Works – Step-by-Step
Quick Sort follows the divide-and-conquer approach to sort elements efficiently. Here’s a step-by-step breakdown of how it works:
- Choose a Pivot Element: Select one element from the array to act as the pivot. This can be the first element, last element, middle element, or even chosen randomly. The pivot helps in dividing the array.
- Partition the Array: Rearrange the elements so that:
- All elements less than the pivot are moved to its left.
- All elements greater than the pivot are moved to its right C++ Vectors.
- The pivot is now in its correct sorted position.
- Recursively Apply Quick Sort: Repeat the same process (choose pivot → partition → sort) on the left and right sub-arrays (excluding the pivot).
- Base Case (Stop Condition): The recursion stops when sub-arrays have zero or one element, as they are already sorted.
- First Element: Simple but can lead to worst-case performance on sorted arrays.
- Last Element: Similar risks as the first element.
- Random Element: Reduces the chances of worst-case behavior by randomizing input.
- Median-of-Three: Choose the median of the first, middle, and last elements to improve balance.
- int partition(int[] arr, int low, int high) {
- int pivot = arr[high];
- int i = low – 1;
- for (int j = low; j < high; j++) {
- if (arr[j] < pivot) {
- i++;
- swap(arr, i, j);
- }
- }
- swap(arr, i + 1, high);
- return i + 1;
- }
- void quickSort(int[] arr, int low, int high) {
- if (low < high) {
- int pi = partition(arr, low, high);
- quickSort(arr, low, pi – 1);
- quickSort(arr, pi + 1, high);
- }
- }
- O(log n) for best/average case (due to recursive call stack)
- O(n) in the worst case
Would You Like to Know More About Web Developer? Sign Up For Our Web Developer Courses Now!
Choosing a Pivot Element
The choice of pivot is critical to Quick Sort’s performance. Several strategies exist:
A poor pivot choice can lead to imbalanced partitions and degrade performance to O(n²), while a good pivot leads to optimal partitioning and performance Backtracking Programming .
Partitioning the Array
Partitioning is the heart of Quick Sort Algorithm. During partitioning, the pivot element is positioned in its correct place in the sorted array. Elements smaller than the pivot are moved to its left, and elements larger are moved to its right Web Designing & Development Training. A commonly used partitioning algorithm is Lomuto’s partition scheme, which is easier to implement, and Hoare’s scheme, which is faster and uses fewer swaps.
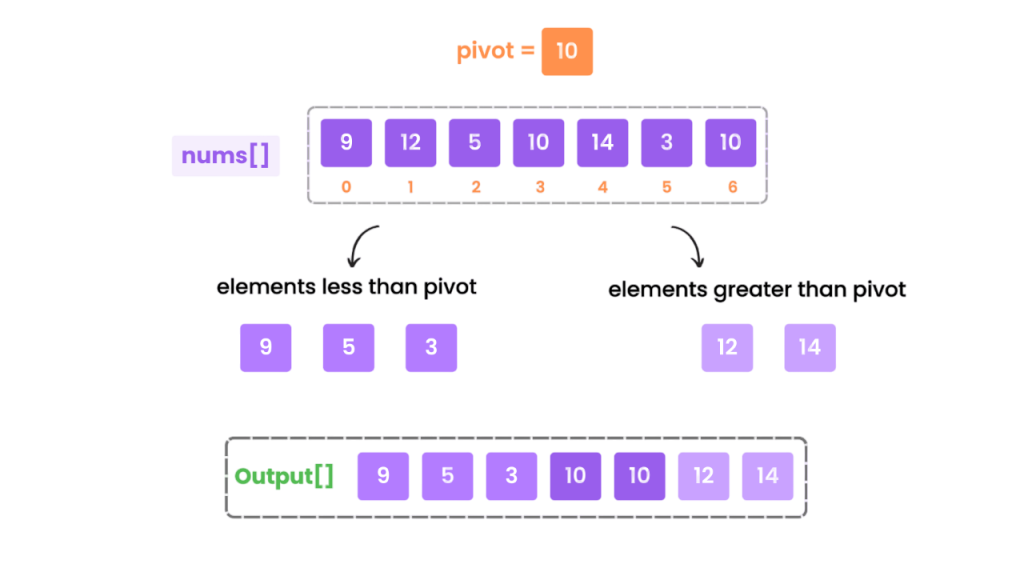
Lomuto Partition (using the last element as pivot):
This partitioning ensures that the pivot is in the correct sorted position.
Are You Interested in Learning More About Web Developer? Sign Up For Our Web Developer Courses Today!
Recursive Implementation of Quick Sort
Here is a basic recursive implementation of Quick Sort in Java-like pseudocode:
The recursion continues until the base case is reached where low >= high, meaning the subarray has one or no elements, and thus is already sorted Height of a Tree.
Time and Space Complexity Analysis
Time Complexity:
| Scenario | Time Complexity |
|---|---|
| Best Case | O(n log n) |
| Average Case | O(n log n) |
| Worst Case | O(n²) |
In the best and average cases, the pivot splits the array evenly, leading to log n levels of recursion with n operations per level C Programming Examples. In the worst case, such as when the array is already sorted and the smallest or largest element is always chosen as pivot, the recursion depth becomes n, resulting in O(n²) complexity.
Space Complexity:
Unlike Merge Sort, Quick Sort is in-place and does not require additional arrays.
Best Case, Worst Case, and Average Case
Best Case:
The pivot splits the array into two equal halves repeatedly. This results in a balanced recursion tree, giving O(n log n) performance.
Average Case:
Assuming random pivot selection, the division will generally be well-balanced. Average-case time complexity also results in O(n log n) Minimum Spanning Tree.
Worst Case:
Occurs when the pivot always selects the smallest or largest element, causing unbalanced partitions and leading to O(n²) performance. This can happen with sorted or reverse-sorted input if pivot selection is naive.
Conclusion
Quick Sort is one of the most efficient and widely used sorting algorithms, especially for large datasets. Its divide-and-conquer approach, combined with in-place sorting and average-case time complexity of O(n log n), makes it a preferred choice in many real-world applications. Despite its worst-case time complexity of O(n²), this scenario can often be avoided with good pivot selection strategies, such as using the median or a randomized pivot. Understanding how Quick Sort works from selecting a pivot, partitioning the array, and applying recursion provides valuable insights into problem-solving techniques and recursive thinking. It’s also an important topic for technical interviews, where algorithm efficiency and clarity of implementation are key. While algorithms like Merge Sort guarantee better worst-case performance, Web Designing & Development Training Quick Sort is often faster in practice due to lower overhead and in-place operation, which reduces memory usage. In summary, mastering Quick Sort is essential for anyone learning data structures and algorithms (DSA). It not only strengthens your grasp of recursion and sorting techniques but also helps build a solid foundation for tackling more advanced algorithmic problems.





