
- Introduction to Merge Sort
- Why Merge Sort? – Use Cases and Benefits
- How Merge Sort Works – Divide and Conquer Approach
- Merge Sort Pseudocode and Flowchart
- Recursive Implementation of Merge Sort
- Iterative Implementation of Merge Sort
- Merging Two Sorted Arrays – Core Step
- Conclusion
Introduction to Merge Sort
Merge Sort Algorithm is one of the most efficient and popular sorting algorithms based on the divide-and-conquer paradigm. It is a comparison-based, stable sorting algorithm that guarantees a time complexity of O(n log n) regardless of the input data. It splits the input array into two halves, recursively sorts each half, and then merges the sorted halves into one sorted array. Merge Sort was invented by John von Neumann in 1945 and is still widely used in practice, especially when dealing with large data sets or data stored externally. Because of its predictable performance and stability, it is a reliable choice in scenarios that require guaranteed performance. Merge Sort is a popular and efficient sorting algorithm based on the divide-and-conquer technique Web Designing & Development Training. It works by dividing an unsorted list into smaller sublists until each sublist contains only one element, which is naturally sorted. Then, it merges these sublists step by step to produce new sorted sublists until a single sorted list is obtained. This merging process ensures that the resulting list is ordered correctly. Merge Sort has a consistent time complexity of O(n log n), making it highly efficient for large datasets compared to simpler algorithms like Bubble Sort or Insertion Sort. It is a stable sort, meaning it preserves the relative order of equal elements, which can be important in certain applications. One of the key advantages of Merge Sort Algorithm is its predictable performance, as its time complexity remains the same regardless of the input’s initial order. However, it does require additional memory space for the temporary arrays used during the merge process, which can be a drawback in memory-constrained environments. Merge Sort is widely used in software libraries and systems where stability and performance are essential. Its systematic approach and reliable efficiency make it a fundamental concept in computer science and a crucial algorithm for students and developers to understand.
To Earn Your Web Developer Certification, Gain Insights From Leading Data Science Experts And Advance Your Career With ACTE’s Web Developer Courses Today!
Why Merge Sort? – Use Cases and Benefits
Merge Sort is suitable for a variety of use cases. Here are some reasons to prefer Merge Sort:
- Large datasets: Because of its consistent O(n log n) time complexity, it is very efficient even with millions of elements.
- Stable sorting: Merge Sort maintains the relative order of equal elements, which is crucial in applications like multi-key sorting.
- Linked lists: Unlike quicksort, merge sort doesn’t require random access, making it ideal for sorting linked lists Software Engineering Prototype .
- External sorting: It is used for sorting huge files stored in external memory (disk), where reading data in chunks is more efficient.
- Multithreaded applications: The divide phase of Merge Sort can be parallelized easily.
- Predictable time complexity.
- Stable sort.
- Good for parallel execution.
- Works well with linked structures.
- Divide: The array is divided into two halves until subarrays of size 1 are obtained. A single-element array is considered sorted.
- Conquer: The smaller sorted arrays are recursively merged to produce new sorted arrays.
- Combine: The final sorted array is obtained by merging all sorted subarrays in the correct order.
- Let’s take the array: [38, 27, 43, 3, 9, 82, 10]
- Divide: [38, 27, 43, 3] and [9, 82, 10]
- Further divide: [38, 27] and [43, 3] etc.
- if left < right:
- mid = (left + right) / 2
- MERGE_SORT(arr, left, mid)
- MERGE_SORT(arr, mid + 1, right)
- MERGE(arr, left, mid, right)
- Create temporary arrays L and R
- Copy data to L and R
- Merge the temporary arrays back into arr
- void merge(int arr[], int l, int m, int r) {
- int n1 = m – l + 1;
- int n2 = r – m;
- int* L = new int[n1];
- int* R = new int[n2];
- for (int i = 0; i < n1; i++)
- L[i] = arr[l + i];
- for (int j = 0; j < n2; j++)
- R[j] = arr[m + 1 + j];
- int i = 0, j = 0, k = l;
- while (i < n1 && j < n2) {
- if (L[i] <= R[j])
- arr[k++] = L[i++];
- else
- arr[k++] = R[j++];
- }
- while (i < n1) arr[k++] = L[i++];
- while (j < n2) arr[k++] = R[j++];
- delete[] L;
- delete[] R;
- }
- void mergeSort(int arr[], int l, int r) {
- if (l < r) {
- int m = l + (r – l) / 2;
- mergeSort(arr, l, m);
- mergeSort(arr, m + 1, r);
- merge(arr, l, m, r);
- }
- }
- void mergeSortIterative(int arr[], int n) {
- for (int curr_size = 1; curr_size <= n - 1; curr_size = 2 * curr_size) {
- for (int left_start = 0; left_start < n - 1; left_start += 2 * curr_size) {
- int mid = min(left_start + curr_size – 1, n – 1);
- int right_end = min(left_start + 2 * curr_size – 1, n – 1);
- merge(arr, left_start, mid, right_end);
- }
- }
- }
- vector
mergeSortedArrays(vector & a, vector & b) { - int i = 0, j = 0;
- vector
result; - while (i < a.size() && j < b.size()) {
- if (a[i] < b[j])
- result.push_back(a[i++]);
- else
- result.push_back(b[j++]);
- }
- while (i < a.size()) result.push_back(a[i++]);
- while (j < b.size()) result.push_back(b[j++]);
- return result;
- }
Key Benefits:
How Merge Sort Works – Divide and Conquer Approach
Merge Sort follows the classic divide-and-conquer methodology:
This recursive decomposition continues until all subarrays are merged. The merging process is the key step that ensures the final sorted output What is Software Engineering.
Example:
The merge phase starts from the smallest units.
Would You Like to Know More About Web Developer? Sign Up For Our Web Developer Courses Now!
Merge Sort Pseudocode and Flowchart
Pseudocode:
Merge Sort is a divide-and-conquer algorithm that sorts an array by dividing it into two halves, recursively sorting each half, and then merging the two sorted halves into a single sorted array. It divides the problem of sorting a large array into smaller, easier-to-manage subproblems Exploring Software Engineering, which makes it very efficient with a guaranteed time complexity of O(n log n).
MERGE_SORT(arr[], left, right):
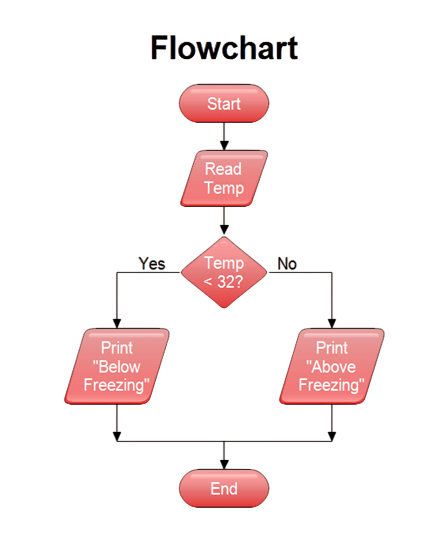
MERGE(arr[], left, mid, right):
Recursive Implementation of Merge Sort in C++
Recursive Merge Sort is a classic divide-and-conquer sorting algorithm that works by recursively splitting an array into two halves until each subarray contains a single element, which is inherently sorted Web Designing & Development Training. Then, it merges these smaller sorted subarrays step-by-step to form larger sorted arrays until the entire array is sorted.
Are You Interested in Learning More About Web Developer? Sign Up For Our Web Developer Courses Today!
Iterative Implementation of Merge Sort
Unlike the recursive approach, the iterative merge sort sorts the array by progressively merging pairs of subarrays of increasing size. It starts by merging subarrays of size 1, then size 2, then size 4, and so on StringBuilder , doubling the size each iteration until the entire array is sorted. This bottom-up approach avoids recursion by using loops.
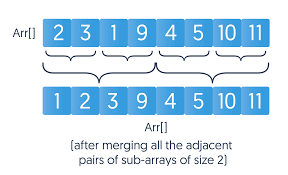
Merging Two Sorted Arrays – Core Step
Merging two sorted arrays involves comparing the elements of both arrays one by one and placing the smaller element into a new array Pointers in C . This process continues until all elements from both arrays are merged in sorted order.
This merging step ensures that the result is always sorted if the input arrays are sorted.
Conclusion
In conclusion, Merge Sort Algorithm is a powerful and reliable sorting algorithm that exemplifies the divide-and-conquer strategy. Its systematic process of breaking down a list into smaller parts, sorting them individually, and then merging them ensures a high level of efficiency, especially for large datasets. With a guaranteed time complexity of O(n log n) in all cases best, average, and worst it stands out as one of the most consistent and predictable sorting algorithms. Its stability makes it particularly valuable in scenarios where maintaining the relative order of equal elements is important Web Designing & Development Training , Merge Sort Pseudocode such as in databases or multi-key sorting operations. Although Merge Sort requires additional memory for temporary arrays during the merging phase, the trade-off is often justified by its performance and reliability. It is especially useful in external sorting, where data does not fit into memory and must be sorted using storage devices like hard drives. Due to its robust nature, Merge Sort is commonly used in various software libraries and real-world applications. Understanding Merge Sort is essential for anyone studying algorithms and computer science, as it introduces important concepts like recursion, time complexity analysis, and the efficiency of divide-and-conquer methods. Overall, Merge Sort remains a foundational and widely respected algorithm in the field of computing.





