How to Check If a Number Is Prime in C Programming

What is a Prime Number?

A prime number is a natural number greater than 1 that has exactly two distinct positive divisors: 1 and itself. In other words, a prime number cannot be divided evenly by any other number except 1 and the number itself. For example, 2, 3, 5, 7, 11, and 13 are all prime numbers. The number 2 is the smallest and the only even prime number because every other even number can be divided by 2, making them composite. Prime numbers play a fundamental role in mathematics, especially in number theory, because they are considered the “building blocks” of whole numbers. Every number greater than 1 can be expressed as a product of prime numbers in a unique way Web Designing Training. This is known as the Fundamental Theorem of Arithmetic. Numbers that have more than two positive divisors are called composite numbers. For example, 4, 6, 8, and 9 are composite because they can be divided by numbers other than 1 and themselves. Prime numbers are also crucial in modern computer science and cryptography, particularly in securing data through encryption algorithms such as RSA, which rely on the difficulty of factoring large prime numbers. Their importance makes them a key topic in both theoretical and applied mathematics.

To Earn Your Web Developer Certification, Gain Insights From Leading Data Science Experts And Advance Your Career With ACTE’s Web Developer Courses Today!

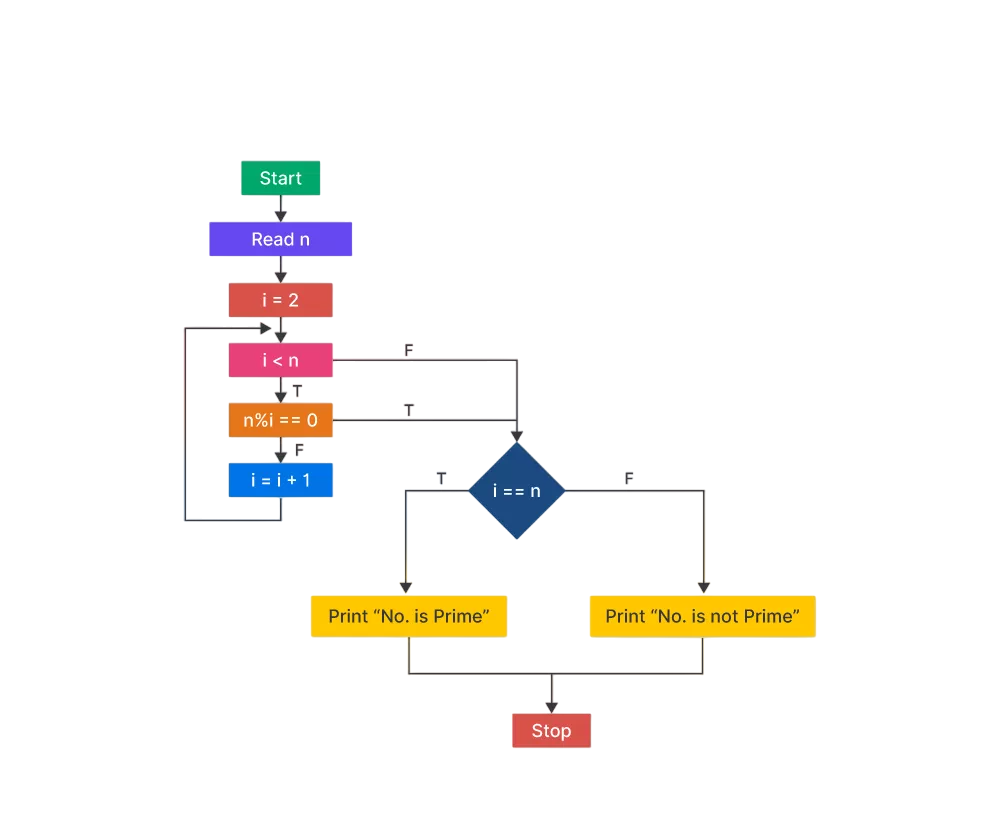
Logic for Prime Number Detection

• Start With Input Validation: Check if the input number is greater than 1. Numbers less than or equal to 1 are not prime by definition.
• Handle the Smallest Prime Separately: The number 2 is the smallest and only even prime number. If the input is 2, it’s prime.
• Eliminate Even Numbers Greater Than 2: Any even number greater than 2 is not prime because it’s divisible by 2 Software Engineering Prototype .
• Loop From 3 to √n: To check for factors, loop from 3 up to the square root of the number (√n). If no factor is found in this range, the number is prime.
• Check Divisibility: In the loop, check if the number is divisible by any odd number in the range. If it is, it’s not a prime.



• Use Modulo Operator (%): Use n % i == 0 to check if the number divides evenly (i.e., no remainder). If true, it’s not a prime.
• Optimize by Skipping Even Checks: After checking for 2, increment the loop by 2 (i.e., check only odd numbers) to improve efficiency.
• Return Result Based on Factor Check: If no divisors are found, return true (prime); otherwise, return false (not prime).

Subscribe To Contact Course Advisor

Subscribe

Writing the Program in C

Simple C Program:

• #include
• int main() {
• int num, i, isPrime = 1;
• printf(“Enter a number: “);
• scanf(“%d”, &num);
• if (num <= 1) {
• isPrime = 0;
• } else {
• for (i = 2; i < num; i++) {
• if (num % i == 0) {
• isPrime = 0;
• break;
• }
• }
• }
• if (isPrime)
• printf(“%d is a prime number.\n”, num);
• else
• printf(“%d is not a prime number.\n”, num);
• return 0;

Would You Like to Know More About Web Developer? Sign Up For Our Web Developer Courses Now!

Optimizing the Logic

Optimizing the logic for prime number detection is essential, especially when working with large numbers or running multiple checks in a loop. The most basic approach involves checking whether a number is divisible by any integer from 2 to n-1, but this is inefficient. A major optimization is reducing the range of checks to the square root of the number (√n), as any non-prime number must have a factor less than or equal to its square root. What is Software Engineering Another important improvement is skipping even numbers during iteration. Since all even numbers greater than 2 are not prime, it’s more efficient to check only odd numbers after handling the special case of 2. This significantly cuts down the number of iterations. Additionally, we can stop the loop immediately when a divisor is found, preventing unnecessary checks. For further performance in large-scale applications, using algorithms like the Sieve of Eratosthenes can help generate prime numbers efficiently. In coding terms, using proper data types and avoiding redundant calculations (like repeated square root evaluations inside loops) can also improve execution speed. By applying these optimizations, prime detection becomes much faster and more suitable for use in cryptography, number theory, or any application involving large numeric computations.

Optimized Version

• #include
• #include
• int main() {
• int num, i, isPrime = 1;
• printf(“Enter a number: “);
• scanf(“%d”, &num);
• if (num <= 1)
• isPrime = 0;
• else {
• for (i = 2; i <= sqrt(num); i++) {
• if (num % i == 0) {
• isPrime = 0;
• break;
• }
• }
• }
• if (isPrime)
• printf(“%d is prime.\n”, num);
• else
• printf(“%d is not prime.\n”, num);
• return 0;
• }

Develop Your Skills with Web Developer Certification Course

Weekday / Weekend BatchesSee Batch Details

Checking for Edge Cases

• Number Less Than 2: Any number less than 2 (like 0, 1, or negative numbers) is not prime by definition.
• Number Equals 2: The number 2 is a special case: it’s the smallest and only even prime number. Web Designing Training It should be handled separately.
• Even Numbers Greater Than 2: All even numbers greater than 2 are not prime since they are divisible by 2.



• Floating-Point or Non-Integer Input: Prime numbers are defined only for positive integers, so reject or round inputs like 3.5, strings, or characters.
• Large Numbers: When dealing with large integers, ensure the algorithm is efficient (e.g., loop only up to √n) and handles performance issues.
• Non-Numeric Input: Inputs like strings (“abc”), null, or undefined should be validated and rejected before processing for primality.

Are You Interested in Learning More About Web Developer? Sign Up For Our Web Developer Courses Today!

Loop-Based Method

This method uses a loop and checks divisibility Exploring Software Engineering:

• for (i = 2; i <= num / 2; i++) {
• if (num % i == 0) {
• isPrime = 0;
• break;
• }
• }

Simple

• Easy to understand
• Good for small inputs

However, not the most efficient for large numbers.

Web Development Sample Resumes! Download & Edit, Get Noticed by Top Employers! Download

Function-Based Prime Check

A function-based approach to prime number checking involves encapsulating the logic for determining whether a number is prime into a reusable and modular function. This method enhances code readability, maintainability, and reusability across applications. Typically, the function accepts a number as input and returns a boolean value true if the number is prime and false otherwise. Inside the function, basic validations are performed first, such as checking if the number is less than 2 (not prime) or equal to 2 (prime). For numbers greater than 2, the function usually checks for divisibility from 2 up to the square root of the number, Throw and Throws Java as any non-prime will have at least one factor in that range. To optimize, even numbers greater than 2 can be excluded early, and only odd divisors need to be checked. The function structure keeps the logic isolated, allowing easy integration into larger applications, such as number theory tools, security systems, or coding challenges. Additionally, it can be enhanced with edge case handling and performance tuning for checking large numbers. By using a function-based design, developers can avoid redundancy and ensure consistent behavior when verifying primes across different parts of a program.

Function Example:

• int isPrime(int n) {
• if (n <= 1) return 0;
• for (int i = 2; i <= sqrt(n); i++) {
• if (n % i == 0) return 0;
• }
• return 1;
• }

Conclusion

Identifying prime numbers in C is one of the best ways to practice fundamental programming skills like loops, conditionals, and functions. Starting with a basic brute-force approach and gradually optimizing with sqrt(n) logic helps understand performance and time complexity. By modularizing code into functions and exploring common use cases like prime series generation, you gain insight into both real-world problem-solving and interview preparation.Detecting prime numbers through a function-based approach offers a clean, Web Designing Training efficient, and reusable way to solve a common mathematical problem in programming. By encapsulating the logic within a function, developers can simplify their code, handle edge cases effectively, and optimize performance especially when working with large numbers or repeated checks. This method not only improves code readability but also lays a strong foundation for more advanced applications in areas like cryptography, data validation, Loop-Based Method and algorithm design. Whether you’re a beginner or an experienced developer, mastering prime number detection using functions is a valuable and practical skill in problem-solving.