Last updated on 09th Aug 2025| 11224
(5.0) |48874 Ratings
E-mail this post
- Introduction to Model Evaluation
- What is Cross Validation?
- Techniques of Cross Validation
- K-Fold Cross Validation Explained
- Stratified K-Fold
- Leave-One-Out Cross Validation (LOOCV)
- Time Series Cross Validation
- Bias-Variance Tradeoff
- Implementing Cross Validation in Python
- Common Pitfalls
- Conclusion
Introduction to Model Evaluation
Model evaluation is essential for understanding how well predictive models work. It ensures that these models generalize to new data instead of just memorizing patterns from the training set. Practitioners know that good performance on training data doesn’t always mean good performance in the real world. This understanding helps them spot issues like overfitting, where a model is too focused on the training data, or underfitting, where the model is too simple. By evaluating models using important metrics tailored to different problem types, practitioners can make better choices. For example, they use accuracy, precision, recall, and F1-score for classification. For regression, they rely on MSE and RMSE. This systematic approach allows practitioners to select between competing models and adjust hyperparameters, leading to stronger and more reliable predictive solutions.
Ready to Get Certified in Machine Learning? Explore the Program Now Machine Learning Online Training Offered By ACTE Right Now!
What is Cross‑Validation?
Cross-validation (CV) is a strong resampling method that splits data into several training and testing sets.
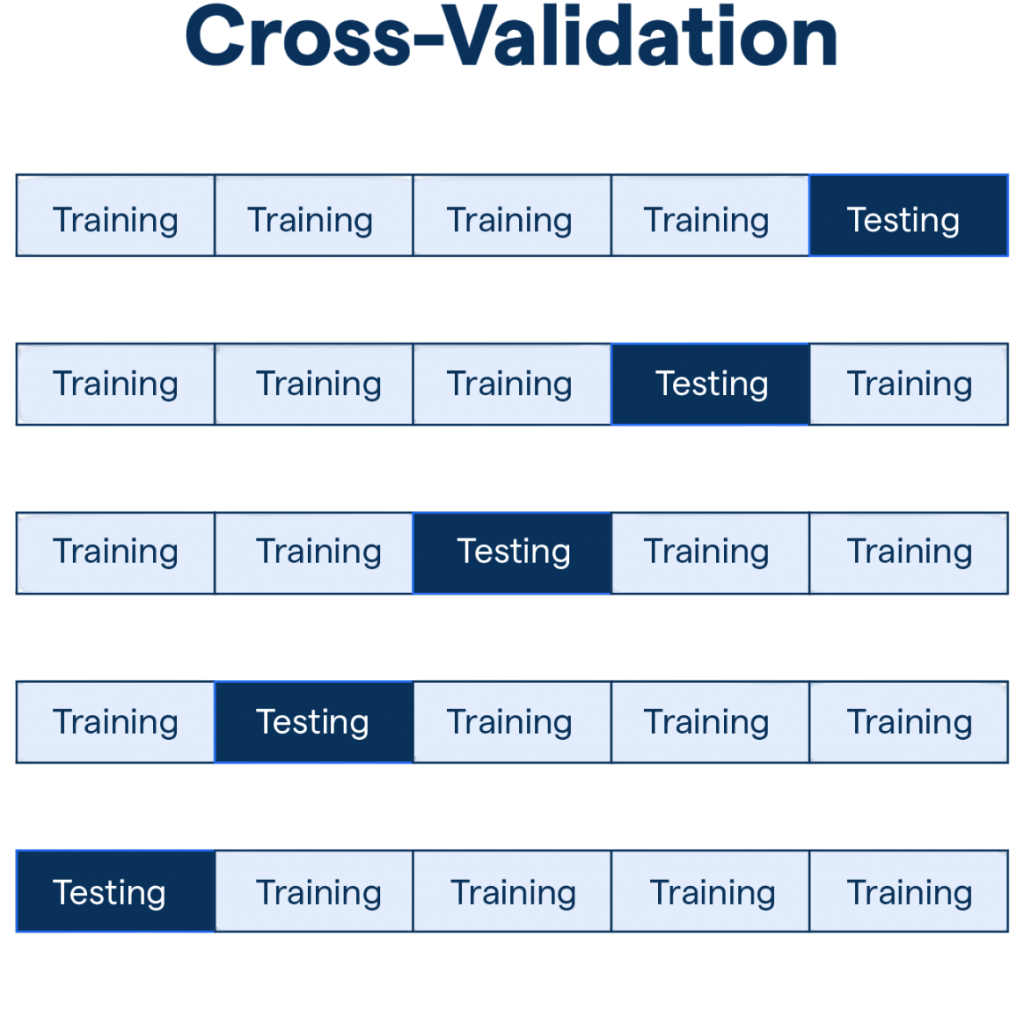
This approach helps estimate performance more effectively. By using all available data points across different parts, CV gives a more trustworthy and detailed view of model performance. This method lowers the variability in performance estimates and reduces the chance of overfitting. Overfitting can happen when researchers and data scientists depend on just one train-test split. The technique offers a more complete and reliable evaluation of predictive models, making it a crucial tool for confirming analytical methods with increased confidence and accuracy.
Techniques of Cross Validation
Common CV Techniques:
- Holdout Validation: One train-test split.
- K‑Fold Cross‑Validation: Divides data into k folds.
- Stratified K‑Fold: Ensures label distribution consistency in classification.
- Leave-One-Out CV (LOOCV): Extreme form of k-fold where k = n.
- Time Series CV: Maintains temporal order for sequential data.
- Split data into k equal-sized folds (e.g., k = 5).
- Use k‑1 folds for training.
- Use the remaining fold for testing.
- Repeat k times so each fold is used once as the test set.
- Average the evaluation metric across all folds.
- Makes efficient use of data.
- Reduces variance compared to simple holdout.
- More stable performance estimate.
- Greater computational cost (training k models).
- Data leakage risk if not properly handled.
- Forward‑chaining or rolling window.
- Maintain chronological order in train/test splits.
- Train on [t₁], test on [t₂].
- Train on [t₁, t₂], test on [t₃].
- Continue forward
- Prevents “future-leakage.”
- Suits modeling sequential dependencies.
- Fewer training points in early folds may reduce reliability.
- More complex implementation.
- Bias: Error from erroneous assumptions in the model. High bias → underfitting.
- Variance: Error from sensitivity to fluctuations in training data. High variance → overfitting.
- Irreducible Error: Noise inherent in real-world data.
- import numpy as np
- from sklearn.model_selection import KFold
- from sklearn.metrics import mean_squared_error
- from sklearn.linear_model import Ridge
- X, y = np.random.randn(100, 5), np.random.randn(100)
- kf = KFold(n_splits=5, shuffle=True, random_state=42)
- errors = []
- for train_idx, test_idx in kf.split(X):
- model = Ridge()
- model.fit(X[train_idx], y[train_idx])
- y_pred = model.predict(X[test_idx])
- errors.append(mean_squared_error(y[test_idx], y_pred))
- print(“5-Fold MSE:”, np.mean(errors))
- from sklearn.model_selection import StratifiedKFold
- from sklearn.tree import DecisionTreeClassifier
- from sklearn.metrics import accuracy_score
- from sklearn.datasets import load_iris
- X, y = load_iris(return_X_y=True)
- skf = StratifiedKFold(n_splits=5)
- scores = []
- for train_idx, test_idx in skf.split(X, y):
- clf = DecisionTreeClassifier()
- clf.fit(X[train_idx], y[train_idx])
- scores.append(accuracy_score(y[test_idx], clf.predict(X[test_idx])))
- print(“Stratified 5-Fold Acc:”, np.mean(scores))
- from sklearn.model_selection import TimeSeriesSplit
- from sklearn.ensemble import RandomForestRegressor
- from sklearn.metrics import mean_squared_error
- X, y = get_time_series_data()
- tscv = TimeSeriesSplit(n_splits=5)
- scores = []
- for train_idx, test_idx in tscv.split(X):
- model = RandomForestRegressor()
- model.fit(X[train_idx], y[train_idx])
- scores.append(mean_squared_error(y[test_idx], model.predict(X[test_idx])))
- print(“TimeSeries CV MSE:”, np.mean(scores))
- Data Leakage: Prior preprocessing (e.g., scaling) must be fitted only on training data within each fold.
- Leaky Features: Using features that contain future info invalidates performance estimates.
- Shuffling Time Series: Always maintain temporal order in time series splits.
- Imbalanced Folds: Not stratifying classification tasks can skew results.
- Misaligned Metrics: Choose evaluation metrics appropriate to the problem (e.g. don’t use MSE for classification).
To Explore Machine Learning in Depth, Check Out Our Comprehensive Machine Learning Online Training To Gain Insights From Our Experts!
K‑Fold Cross‑Validation Explained
How It Works:
Advantages:
Drawbacks:
Stratified K‑Fold
Stratified K-Fold is a strong cross-validation method designed for classification tasks, especially when dealing with imbalanced datasets. It ensures that each fold keeps a similar class distribution to the original dataset. This method creates smaller groups that truly represent the data’s characteristics. It gives data scientists more trustworthy estimates when working with datasets that have uneven class proportions. This makes it a valuable tool in machine learning. While it works well for classification, it has drawbacks in regression situations and needs careful management with very small classes. Scikit-learn’s default setup offers a simple way for data scientists to use this reliable validation method, allowing them to make better assessments of model performance across various and difficult datasets.
Leave‑One‑Out CV (LOOCV)
Leave-One-Out Cross-Validation (LOOCV) represents an advanced statistical technique that maximizes data utilization by treating each individual data point as a unique test set. In this method, the algorithm systematically trains on all but one sample and tests performance on the excluded data point, repeating this process for every observation in the dataset. While LOOCV provides unbiased performance estimates by leveraging the entire dataset for validation, it poses significant computational challenges, particularly for large datasets. This approach ensures comprehensive model evaluation by generating n separate models, where n represents the total number of samples, and researchers average their results. However, researchers must carefully weigh its benefits against potential drawbacks, such as high computational complexity and increased variance in error estimation due to testing on extremely small subsets. Despite these limitations, researchers consider LOOCV a powerful validation strategy for understanding model generalizability and performance across diverse datasets.
Looking to Master Machine Learning? Discover the Machine Learning Expert Masters Program Training Course Available at ACTE Now!
Time Series Cross Validation
Standard CV assumes data points are independent, which fails for time series data.
Methods:
Example:
Pros:
Cons:
Bias‑Variance Tradeoff
Understanding Cross-Validation Requires Grasping the Bias-Variance Tradeoff:
Preparing for Machine Learning Job Interviews? Have a Look at Our Blog on Machine Learning Interview Questions and Answers To Ace Your Interview!
Implementing Cross‑Validation in Python
Using scikit-learn, here are examples:
K‑Fold
Stratified K‑Fold (Classification)
Time Series CV
Common Pitfalls
Cross-Validation Pitfalls:
Conclusion
Cross-validation is the cornerstone of trustworthy model evaluation. By intelligently choosing an appropriate CV strategy whether it’s K‑Fold, Stratified, LOOCV, or Time Series you ensure robust, unbiased estimates of model performance. Understanding the bias-variance tradeoff helps in tuning complexity to achieve optimal generalization. Practical implementation in Python (via scikit-learn) shows that following best practices (pipelines, stratification, nested CV) and avoiding common pitfalls (leakage, misaligned metrics) are essential. These strategies contribute to the development of reliable, resilient, and trustworthy machine learning systems.
