Last updated on 06th Aug 2025| 10931
(5.0) |48874 Ratings
E-mail this post
- What is Regularization?
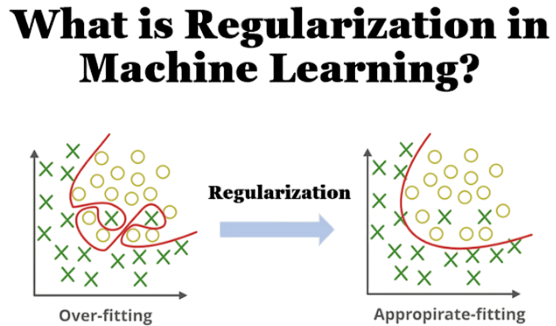
- Overfitting vs Underfitting
- L1 Regularization (Lasso)
- L2 Regularization (Ridge)
- Elastic Net
- Dropout in Neural Networks
- Early Stopping
- Data Augmentation as Regularization
- Cross-validation with Regularization
- Impact on Model Generalization
- Regularization in Logistic and Linear Regression
- Conclusion
What Is Regularization?
Regularization in Machine Learning is a widely used technique designed to prevent models from fitting noisy patterns in training data commonly known as overfitting by introducing additional constraints or penalties during the learning process. Its main goal is to improve generalization, enabling models to deliver accurate predictions on new, unseen data rather than just memorizing training examples.
Without regularization, complex models like deep neural networks with millions of parameters or polynomial regressors with many features can fit the training set extremely well. However, this comes at the cost of capturing spurious patterns that don’t generalize, leading to poor performance on test sets. Regularization counteracts this tendency by penalizing complex configurations, effectively enforcing a smoother or simpler representation of the underlying function.
Do You Want to Learn More About Database? Get Info From Our Database Online Training Today!
Overfitting vs Underfitting
Regularization in Machine Learning, researchers understand regularization through the bias-variance tradeoff. This concept shows the balance between model complexity and predictive performance. When data scientists create a model that is too simple, it underfits. The model fails to capture critical data trends and performs poorly on both training and testing sets. For example, a linear regression might try to describe a fundamentally nonlinear relationship. On the other hand, if a model becomes too complex, it risks overfitting. It essentially memorizes noise and specific details from the training data. This leads to high initial accuracy but poor performance on new data. Mathematicians break down the total expected error into bias squared, variance, and irreducible noise. Regularization works to reduce variance while introducing minimal bias. Data scientists can visualize this using a scatter plot. Finding the best model complexity is like selecting a polynomial that captures the data’s underlying structure without following random fluctuations. By using implicit constraints that shape model behavior, like enforcing smoothness, sparsity, or weight control, regularization techniques help data scientists create robust models that generalize well across different datasets.
L1 Regularization (Lasso)
L1 regularization, known as Lasso in regression contexts, augments the loss function with the absolute sum of weights:
- ΩL1(θ)=∑j∣θj∣\Omega_{L1}(\theta) = \sum_j | \theta_j |ΩL1(θ)=j∑∣θj∣
When added to the objective:
- minθ1N∑iℓ(f(xi),yi)+λ∑j∣θj∣\min_\theta \frac{1}{N}\sum_i \ell\big(f(x_i), y_i\big) + \lambda \sum_j |\theta_j|θminN1i∑ℓ(f(xi),yi)+λj∑∣θj∣
L1 regularization encourages many parameters θj\theta_jθj to shrink to exactly zero, effectively performing feature selection. The Lasso is especially useful when:
- Working with high-dimensional data (many predictors, few observations).
- Seeking interpretable models, where unimportant features are automatically dropped.
- Dealing with correlated features Lasso can pick one representative feature from a group.
- ΩL2(θ)=∑jθj2\Omega_{L2}(\theta) = \sum_j \theta_j^2ΩL2(θ)=j∑θj2
- minθ1N∑iℓ(f(xi),yi)+λ∑jθj2\min_\theta \frac{1}{N}\sum_i \ell\big(f(x_i), y_i\big) + \lambda \sum_j \theta_j^2θminN1i∑ℓ(f(xi),yi)+λj∑θj2
- Preventing instability due to large weights
- Reducing multicollinearity effects.
- Ensuring convex optimization (closed-form formulas exist for linear models).
- Split data into training and validation subsets.
- Monitor validation loss each epoch.
- Stop training when validation loss ceases improving (within some patience window).
- Rollback model to the parameters at lowest validation loss
- Images: rotations, flips, shifts, cropping, color transformations.
- Audio: noise injection, time-stretching, pitch shifting.
- NLP: synonym replacement, back-translation, shuffling.
- Split the dataset into kkk folds.
- Train model kkk times, each time holding out one fold as validation.
- Evaluate average validation error to choose the best hyperparameters.
- Reducing variance through model complexity penalties.
- Promoting smoother mappings or decision functions.
- Ensuring better performance under data distribution shifts.
- Models more interpretable: L1 eliminates irrelevant features, dropout smooths predictions.
- Faster convergence: weights don’t blow up.
- Simplified training: early stopping automatically halts without manual intervention.
- Linear Regression: θ=(XTX+λI)−1XTy\theta = (X^T X + \lambda I)^{-1} X^T yθ=(XTX+λI)−1XTy
- The objective is: minθ∑ilog(1+e−yixiTθ)+λΩ(θ)\min_\theta \sum_i \log(1 + e^{-y_i x_i^T \theta}) + \lambda \Omega(\theta)θmini∑log(1+e−yixiTθ)+λΩ(θ)
- Use L2 if many features but co-linear.
- Use L1 if feature selection is needed.
- Use Elastic Net in high-dimensional sparse settings.
Would You Like to Know More About Database? Sign Up For Our Database Online Training Now!
L2 Regularization (Ridge)
L2 Regularization , commonly referred to as Ridge, penalizes the squared magnitude of weights:
Leading to:
Unlike L1 and L2 Regularization does not enforce zero weights; instead, it shrinks all weights uniformly. This helps in:
Ridge regression is stable and performs well in scenarios with noisy data or moderate feature correlation. However, its models remain non-sparse, which can be a disadvantage for interpretability.
Elastic Net
Elastic Net combines L1 and L2 penalties using a tunable parameter α∈[0,1]. This helps balance model complexity and predictive performance. Data scientists use this method to tackle important challenges in Regularization in Machine Learning. It is particularly useful when dealing with highly correlated features or high-dimensional datasets, where traditional methods like Ridge or Lasso regression fall short. The approach spreads weight across feature groups and allows for variable selection. This offers a strong solution that addresses the weaknesses of individual regularization techniques. Researchers apply Elastic Net using algorithms such as coordinate descent and popular libraries like scikit-learn. This provides a powerful tool for creating sparse, yet stable models that have better interpretability and predictive accuracy.
Dropout in Neural Networks
Dropout is a novel stochastic regularization method that Srivastava and colleagues introduced in 2014. It changes how we train deep neural networks by randomly turning off neurons during learning. This method forces neural networks to create stronger and more flexible representations by selectively dropping units. It helps stop complex co-adaptations that can cause overfitting. Essentially, dropout mimics training several smaller networks, which significantly improves how well models perform across various areas, from image classification to natural language processing. During inference, researchers adjust network weights to account for the dropout rate, which helps maintain consistent performance. Dropout is especially effective in fully connected layers that tend to have too many parameters. Its success has led to the development of related techniques like word dropout and attention dropout, making it an important regularization method in today’s Regularization in Machine Learning systems.
To Earn Your Database Certification, Gain Insights From Leading Blockchain Experts And Advance Your Career With ACTE’s Database Online Training Today!
Early Stopping
Early stopping treats the training process itself as a form of regularization:
This prevents overfitting mid-training and requires no changes to the model structure making it a simple yet effective technique, especially in neural network training. Early stopping indirectly controls the model’s effective complexity by halting updates before memorization of noise begins.
Data Augmentation as Regularization
Not all regularization happens in model space; some occur in input space. Data augmentation artificially expands the dataset, injecting variability while preserving semantic meaning.
Augmentation teaches models invariance under transformations and effectively reduces overfitting. Libraries like TensorFlow, PyTorch, and albumentations provide easy augmentation pipelines. Modern augmentation strategies like CutMix, MixUp, and Style Transfer have further enhanced learning by combining samples in feature-rich ways.
Preparing for a Database Job? Have a Look at Our Blog on Database Interview Questions and Answers To Ace Your Interview!
Cross-Validation with Regularization
Regularization techniques involve hyperparameters (e.g., λ\lambdaλ, α\alphaα, dropout rates) that must be tuned for optimal performance. Cross-validation (CV), especially k-fold CV, is the standard methodology:
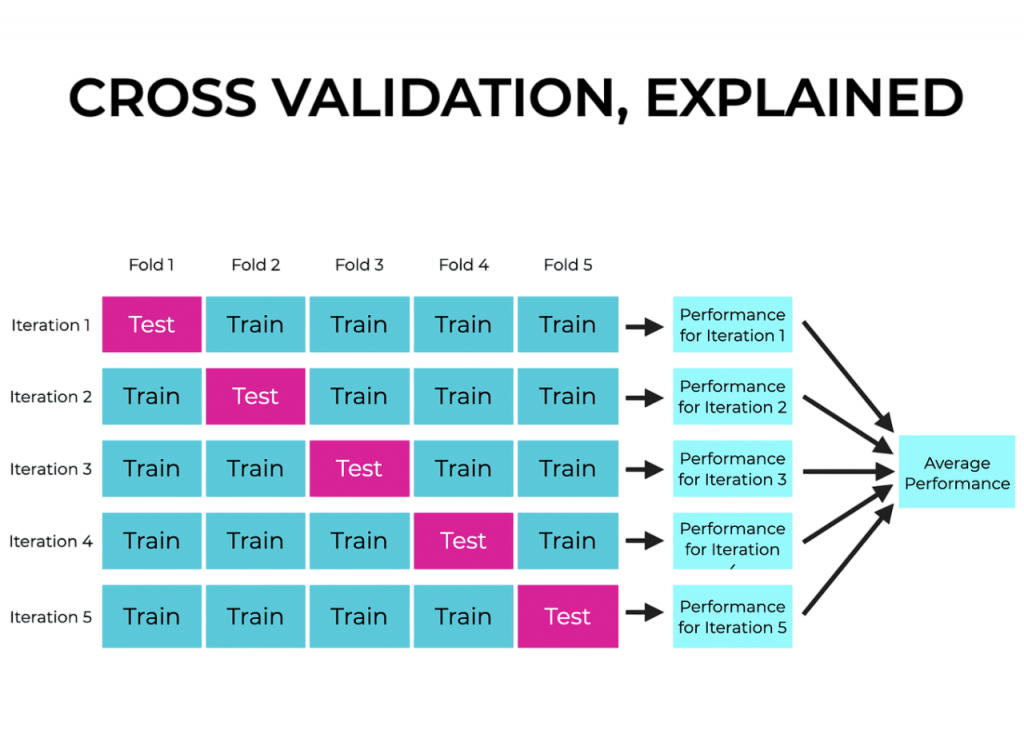
Advanced strategies include nested CV, combining inner loops (for hyperparameter tuning) and outer loops (for performance estimation), ensuring unbiased evaluation. Automation tools like scikit-learn’s GridSearchCV, RandomizedSearchCV, and BayesSearchCV further streamline the selection process, enabling robust, reproducible models with regularization fine-tuned to data characteristics.
Impact on Model Generalization
Regularization dramatically enhances generalization by:
Benefits of Regularization Beyond Accuracy
Researchers and analysts often use techniques like validation curves (validation error vs. model complexity or regularization strength) to visualize performance and detect optimal bias-variance tradeoff.
Regularization in Logistic and Linear Regression
Regularization in Regression Models
Logistic Regression:
Popular Workflow Recommendations:
Conclusion
Regularization is an essential strategy for machine learning professionals. It helps them create reliable and general models that can work well with complex data. Data scientists use various techniques such as L1, L2, Elastic Net, dropout, early stopping, and data augmentation to tackle overfitting from different angles. When researchers apply these methods along with strong cross-validation and established industry practices, they enable Regularization in Machine Learning models to perform better. This approach also helps models stay stable in different data environments and maintain important interpretability, which builds user trust and confidence in algorithmic decision-making.
