How to Use the Percentage Formula in Excel for Accurate Calculations

Understanding Percentages

A percentage represents a number as a fraction of 100. The word “percent” means “per hundred,” so when you say 50%, you’re saying 50 out of 100. Percentages are used to express proportions, rates, and comparisons between numbers. They are commonly used in various fields such as finance, statistics, education, and everyday situations like calculating discounts, interest, or test scores. Understanding how to calculate and interpret percentages helps in making better decisions and analyzing data more effectively. Formula:

• Percentage = (Part / Whole) * 100

This formula is the foundation for many percentage-based calculations. For example, if a student scores 45 out of 50 on a test, the percentage score would be (45/50) * 100 = 90%. Similarly, it can be used to determine percentage increase or decrease in values, such as changes in prices, population, or profits. Developing a strong grasp of percentages enhances numerical literacy and supports better understanding of data-driven insights.

Basic Percentage Formula

The basic percentage formula is used to calculate the percentage of a number:

• Formula: Percentage = (Part / Whole) * 100
• Example: If you have 25 out of 200 students attending a class, the percentage of students attending is:
• Percentage = (25 / 200) * 100 = 12.5%

How to Calculate Percentage Increase and Decrease

A percentage increase or decrease measures the change between two values as a percentage of the original value.

Percentage Increase Formula:

• Percentage Increase = [(New Value – Old Value) / Old Value] * 100
• Example: If a product’s price increases from $50 to $60, the percentage increase is
• Percentage Increase = [(60 – 50) / 50] * 100 = 20%
Percentage Decrease Formula:
• Percentage Decrease = [(Old Value – New Value) / Old Value] * 100
• Example: If a product’s price drops from $80 to $60, the percentage decrease is
• Percentage Decrease = [(80 – 60) / 80] * 100 = 25%

Finding the Percentage of a Total Value

To find the percentage of a total value, multiply the total value by the rate and then divide by 100.

• Formula: Part = (Percentage / 100) * Total
• Example: To find 20% of $200:
• Part = (20 / 100) * 200 = $40

Percentage Change Calculation

Percentage change measures how much something has changed relative to its original value, whether an increase or decrease.

• Formula: Percentage Change = [(New Value – Old Value) / Old Value] * 100
• Example: If a company’s revenue increased from $1,000,000 to $1,250,000:
• Percentage Change = [(1,250,000 – 1,000,000) / 1,000,000] * 100 = 25%/li>

Develop Your Skills with MS Excel Training

Weekday / Weekend BatchesSee Batch Details

Using Excel to Calculate Percentages

Excel provides several methods for calculating percentages.

Basic Percentage Calculation:

• Formula: = (A1 / B1) * 100
• Example: If A1 contains 25 and B1 contains 200, the formula = (A1 / B1) * 100 will return 12.5%.
Percentage Increase/Decrease:
• Formula for percentage increase: = ((New Value – Old Value) / Old Value) * 100
• Formula for percentage change: = ((B1 – A1) / A1) * 100
Percentage of Total Value:
• Formula: = (Percentage / 100) * Total
• Example: If the percentage is in cell A1 and the total value is in B1, the formula would be = (A1 / 100) * B1.

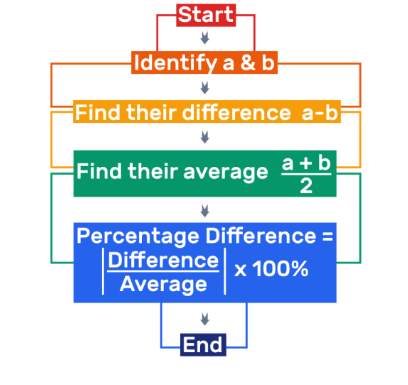
Percentage Difference Between Two Numbers

The percentage difference is used to compare two numbers relative to the average. Formula:

• Percentage Difference = (|Value 1 – Value 2| / [(Value 1 + Value 2) / 2]) * 100
• Example: If you are comparing 50 and 70:
• Percentage Difference = (|50 – 70| / [(50 + 70) / 2]) * 100 = 33.33%

Percentage in Financial Calculations (Discounts, Tax, Profit, Interest)

Percentages are crucial in various financial calculations.

Discounts:

To calculate the discount amount, multiply the original price by the discount percentage.

• Formula: Discount Amount = Original Price * (Discount Percentage / 100)
• Example: A $200 item with a 20% discount:
• Discount Amount = 200 * (20 / 100) = $40
Sales Tax:

To calculate the sales tax, multiply the price by the tax percentage.

• Formula: Sales Tax = Price * (Tax Percentage / 100)
• Example: For a $50 item with 8% sales tax:
Sales Tax = 50 * (8 / 100) = $4 Profit Margin:

The profit margin is the percentage of profit made from selling an item.

• Formula: Profit Margin = (Profit / Selling Price) * 100
• Example: If you sell an item for $150 and make a $30 profit:
Profit Margin = (30 / 150) * 100 = 20% Interest:

Simple interest can be calculated using the formula:

• Formula: Interest = Principal * Rate * Time
• Example: A $1,000 loan at 5% interest for 2 years:
Interest = 1000 * 0.05 * 2 = $100

Converting Fractions and Decimals to Percentage

You can easily convert fractions and decimals to percentages by multiplying by 100.

Fraction to Percentage:

To convert a fraction (like 3/4) into a percentage, divide the numerator by the denominator and multiply by 100.

• Formula: Fraction * 100
• Example: 3/4 * 100 = 75%
Decimal to Percentage: To convert a decimal (like 0.45) to a percentage, multiply the decimal by 100.
• Formula: Decimal * 100
• Example: 0.45 * 100 = 45%

Common Mistakes in Percentage Calculation

Not converting the percentage into a fraction or decimal before calculating.

• Incorrect: 100 * 25% → should be 100 * 0.25 or 100 * (25 / 100)

Misunderstanding of percentage increase/decrease.

• Percentage increase is calculated based on the original value, not the new value.

Forgetting to multiply by 100 when converting to percentages.

• Example: 0.25 should be 0.25 * 100 = 25%

Not handling negative percentages properly.

Real-Life Applications of Percentages

Percentages are used in everyday life and various fields, including

• Shopping: Calculating discounts during sales.
• Finance: Understanding interest rates, investment growth, and loans.
• Health: Understanding BMI or body fat percentage.
• Business: Analyzing profit margins, cost reductions, and sales growth.

Practice Problems for Mastering Percentage Calculations

Find the percentage of 40 in 200.

• Solution: (40 / 200) * 100 = 20%

A product price increased from $50 to $60. Calculate the percentage increase.

• Solution: [(60 – 50) / 50] * 100 = 20%

A $500 item is on sale with a 15% discount. What is the discount amount?

• Solution: 500 * (15 / 100) = $75

Calculate the percentage decrease if a stock price dropped from $200 to $150.

• Solution: [(200 – 150) / 200] * 100 = 25%

You made a $200 profit on a $1,000 investment. Calculate the profit margin.

• Solution: (200 / 1000) * 100 = 20%

By practicing these concepts and formulas, you’ll gain a solid understanding of percentages and be able to apply them confidently in various scenarios!

MS Excel Sample Resumes! Download & Edit, Get Noticed by Top Employers! Download

Conclusion

In conclusion, understanding percentages and their calculations is essential for both academic and real-world applications. Whether you’re analyzing data in Excel or making everyday financial decisions, a solid grasp of percentage concepts can enhance accuracy and efficiency. By applying these skills, you can interpret information more effectively and make informed choices in both personal and professional settings. With consistent practice, these concepts become second nature. Mastering percentages also builds a strong foundation for tackling more advanced mathematical and analytical tasks.