
- Introduction to Game Theory
- The Classic Prisoner’s Dilemma
- Payoff Matrix Explained
- Nash Equilibrium in the Dilemma
- Dominant Strategy
- Iterated Prisoner’s Dilemma
- Tit-for-Tat Strategy
- Real-World Applications (Economics, Politics)
- Conclusion
Introduction to Game Theory
Game theory is a branch of mathematics and economics that studies strategic interactions between rational decision-makers. At its core, game theory provides a structured framework to model competitive and cooperative behaviors In multi-agent Machine Learning Training , scenarios often arise where the outcome for each participant depends not only on their actions but also on the actions of others.From economics and political science to evolutionary biology and computer science, game theory is used to model a wide range of real-world phenomena. The Classic Prisoner’s Dilemma is one of the most iconic and widely analyzed scenarios in game theory, demonstrating how rational agents might fail to cooperate even when it’s in their best interest.Game Theory is the study of strategic decision-making, where the outcome for each participant depends not only on their own choices but also on the choices of others. One of the most famous examples illustrating game theory is the Nash Equilibrium in the Dilemma, which involves two individuals arrested for a crime and interrogated separately. Each prisoner is given the option to either betray the other (defect) or remain silent (cooperate). If both cooperate, they receive a light sentence. If one defects while the other cooperates, the defector goes free while the cooperator gets a harsh sentence. If both defect, they receive moderate sentences. Although mutual cooperation leads to a better collective outcome, rational self-interest often leads both to defect, resulting in a worse outcome for each. This scenario highlights key concepts in game theory such as the Nash Equilibrium, where neither player can improve their outcome by changing their decision alone, and the dominant strategy, which in this case is to defect. The Prisoner’s Dilemma reveals how individual rationality can lead to collective inefficiency, making it a powerful tool for understanding conflict, cooperation, and strategy in fields ranging from economics and politics to cybersecurity and social behavior.
Ready to Get Certified in Machine Learning? Explore the Program Now Machine Learning Online Training Offered By ACTE Right Now!
The Classic Prisoner’s Dilemma
The classic Prisoner’s Dilemma involves two suspects arrested for a crime. They are held in separate cells with no means of communication Recommendations System in Machine Learning. Prosecutors lack sufficient evidence for a conviction unless one confesses.
Each prisoner is given two options:
- Cooperate with the other by remaining silent.
- Defect by betraying the other and confessing.
The outcomes are typically:
- If both cooperate (remain silent): light sentences (e.g., 1 year each).
- If one defects and the other cooperates: the defector goes free, the cooperator gets a heavy sentence (e.g., 10 years).
- If both defect: moderate sentence (e.g., 5 years each).
This dilemma captures the essence of strategic decision-making, where individual rationality leads to a collectively suboptimal outcome.
Payoff Matrix Explained
To visualize the dilemma, game theorists use a payoff matrix:
| Prisoner B Cooperates | Prisoner B Defects | |
|---|---|---|
| Prisoner A Cooperates | A: -1, B: -1 | A: -10, B: 0 |
| Prisoner A Defects | A: 0, B: -10 | A: -5, B: -5 |
Each cell shows the years in prison for A and B respectively. Note that:
- (-1, -1) is the best collective outcome.
- (0, -10) or (-10, 0) is the best individual outcome.
- (-5, -5) is the Nash Equilibrium, where neither can improve by changing strategy unilaterally.
In Machine Learning Training, particularly in areas like reinforcement learning and game-theoretic models, this matrix structure allows analysts to quantify and compare outcomes based on different decisions, enabling predictions about behavior under strategic pressure.
To Explore Machine Learning in Depth, Check Out Our Comprehensive Machine Learning Online Training To Gain Insights From Our Experts!
Nash Equilibrium in the Dilemma
Nash Equilibrium in the Dilemma after mathematician John Nash, a Nash Equilibrium occurs when no player can benefit by changing their strategy while the other keeps theirs unchanged.In the Prisoner’s Dilemma, mutual defection (both prisoners betray each other) is the only Nash Equilibrium. Even though mutual cooperation would yield better collective outcomes, individual incentive to defect dominates.This equilibrium is Pareto inefficient; no one can be made better off without making the other worse off. This demonstrates how rational decision-making can lead to collectively poor outcomes, a theme recurring in economics, F1 Score in Machine Learning Explained international relations, and ecology.n the context of the Prisoner’s Dilemma, the Nash Equilibrium occurs when both prisoners choose to defect, even though mutual cooperation would lead to a better outcome for both. A Nash Equilibrium is a situation where no player can improve their outcome by unilaterally changing their decision, assuming the other player’s choice remains the same. In this case, if one prisoner decides to cooperate while the other defects, the cooperator ends up with a worse sentence. Therefore, both prisoners are incentivized to defect, Tit-for-Tat Strategy since it offers the safest individual payoff regardless of what the other does. Although this outcome is not the best collectively, it is stable; neither prisoner has anything to gain by changing their strategy alone, which is what makes it a Nash Equilibrium.
Dominant Strategy
A strategy is dominant if it is the best choice regardless of what the other player does. In the Prisoner’s Dilemma:
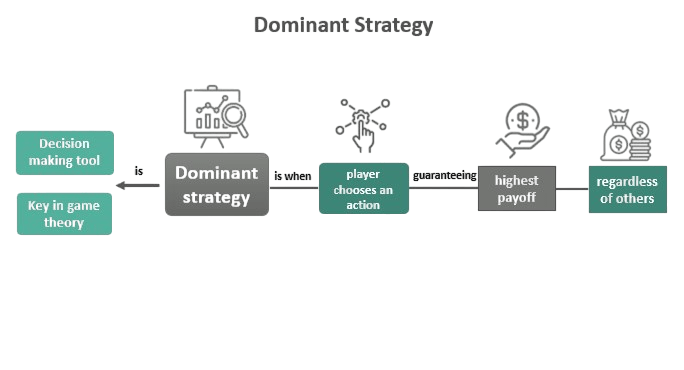
- Defection is dominant for both players.
- No matter what the other player does, defecting always yields a better or equal outcome for an individual.
This rational choice leads to mutual defection, Transfer Learning reinforcing the conflict between individual rationality and collective rationality. It poses critical ethical and strategic challenges in real-world policy design.
Looking to Master Machine Learning? Discover the Machine Learning Expert Masters Program Training Course Available at ACTE Now!
Iterated Prisoner’s Dilemma
Unlike the one-shot version, the Iterated Prisoner’s Dilemma (IPD) allows players to interact repeatedly. This repetition changes incentives dramatically:
- Players can remember past behavior.
- Future punishment or reward becomes possible.
- Cooperation may emerge as a long-term strategy.
In repeated interactions, players often adopt conditional cooperation strategies, rewarding cooperation and punishing defection. The longer the game is expected to last, the more likely cooperation will emerge.This model more closely mirrors real-world relationships like trade, diplomacy, or friendships where repeated interactions incentivize trust and reciprocity.
Tit-for-Tat Strategy
The Tit-for-Tat strategy, Ensemble Learning popularized by Robert Axelrod’s IPD tournaments in the 1980s, became famous for its simplicity and effectiveness:
- Start by cooperating.
- Then mirror the opponent’s last move (cooperate if they cooperated, defect if they defected).
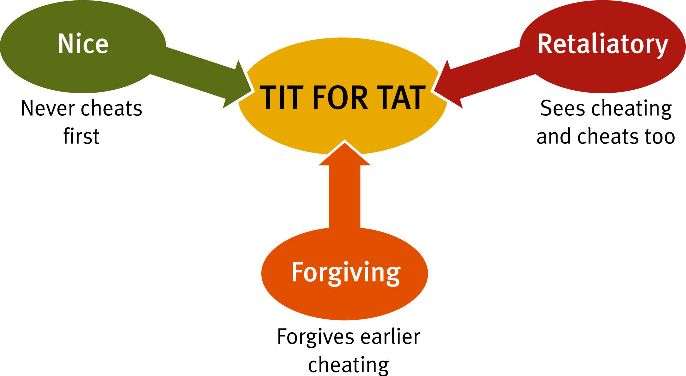
Tit-for-Tat performs well because:
- It is nice: It begins with cooperation.
- It is retaliatory: Punishes defection.
- It is forgiving: Returns to cooperation if the opponent does.
- It is clear: Easy to understand and predict.
Tit-for-Tat promotes reciprocal altruism and fosters trust, essential in long-term strategic relationships
Preparing for Machine Learning Job Interviews? Have a Look at Our Blog on Machine Learning Interview Questions and Answers To Ace Your Interview!
Real-World Applications (Economics, Politics)
The Prisoner’s Dilemma applies to countless real-world scenarios:
Economics:
- Price wars: Two competing firms may both lower prices, harming profits, when both Cyber Extortion could benefit from cooperation (price stability).
- Cartels: Members of a cartel may cheat to increase market share despite agreed production limits.
- Arms races: Countries build up arms fearing the other will defect from peace.
- Climate change: Countries have incentives to let others cut emissions while they maintain economic growth.
Politics:
These examples highlight how individual incentives can derail collective welfare, and why policy and institutions are needed to enforce cooperative outcomes.
Conclusion
In conclusion, the Prisoner’s Dilemma serves as a foundational example in game theory, illustrating how individual rational decisions can lead to suboptimal outcomes for all parties involved. It reveals the tension between personal interest and mutual benefit, highlighting the challenges of trust and cooperation in strategic situations. In Machine Learning Training , especially in multi-agent systems and strategic decision-making models, understanding the dynamics of the Nash Equilibrium in the Dilemma provides valuable insights into real-world scenarios where individuals or agents must make choices without knowing how others will act. This makes game theory an essential tool for analyzing decision-making in economics, politics, cybersecurity, and everyday life.The Classic Prisoner’s Dilemma is a powerful metaphor for understanding strategic conflict and cooperation. From individual decision-making to global policy, it offers insight into why trust breaks down and how it can be rebuilt. Through the lenses of game theory, Tit-for-Tat Strategy, psychology, economics, and AI, this deceptively simple game provides profound lessons on rationality, ethics, and social behavior. Whether modeling AI agents or resolving global climate disputes, the principles embedded in the Prisoner’s Dilemma continue to shape our understanding of cooperation in a competitive world.




