Polynomial Regression | All you need to know [ Job & Future ]

Last updated on 16th Dec 2021, Blog, General

(5.0) | 19472 Ratings 885

Share:

Polynomial Regression is a form of Linear regression known as a special case of Multiple linear regression which estimates the relationship as an nth degree polynomial. Polynomial Regression is sensitive to outliers so the presence of one or two outliers can also badly affect the performance.

• Introduction to polynomial Regression
• Polynomial Regression History
• Characteristics of polynomial Regression
• Alternative Approached
• Procedure to Apply Polynomial Regression
• Why polynomial Regression
• Uses of Polynomial Regression
• What is polynomial regression in machine learning?
• Benefits of polynomial Regression
• Conclusion

Introduction to polynomial Regression:

Polynomial Regression could be a variety of regression during which the connection between the freelance variation of x and therefore the dependence of y is sculptural as ordinal degree polynomial. Polynomial decrease corresponds to the correlation between the worth of x and therefore the corresponding that means with the terms y, mean E (y | x)

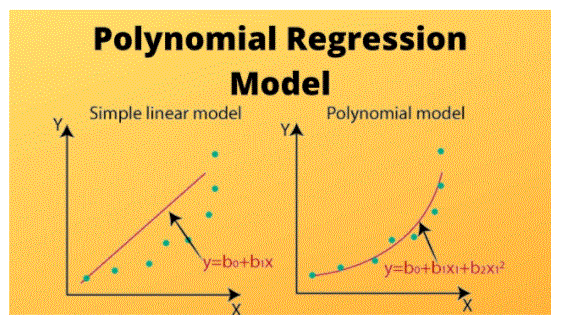
Polynomial Regression History:

Models of polynomial regression are usually balanced using the method of small squares. The smallest square method reduces the variability of the unbalanced coefficient, under the conditions of the Gauss – Markov theorem. The smallest square foot was published in 1805 by Legende and in 1809 by Gauss. The first design for the polynomial retardation test appeared in the 1815 paper Gergonne. In the twentieth century, polynomial retreat played a key role in the development of retrospective analysis, with an emphasis on design issues and specifics. Recently, the use of polynomial models has been supplemented by alternatives, with non-polynomial models having advantages in other categories of problems.

Characteristics of polynomial Regression:

• It is a type of indirect regression method that tells the relationship between independent and dependent variables where the dependent variance is related to the independent difference of the nth degree.
• The most appropriate line is determined by the level of the polynomial regression equation.
• The model taken from the polynomial regression is influenced by outsiders so it is always best to manage outsiders before using the algorithm in the database.
• The Polynomial Feature () function converts to a matrix element depending on the mathematical scale.
The nature of the curve can be researched or visualised using a simple scatter structure that will give you a better idea of ​​the linear relationship between the variables and determine accordingly.

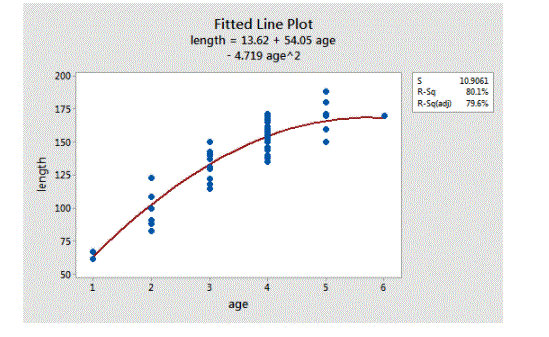
Alternative Approached:

Polynomial retrieval is one example of retrospective analysis victimisation of basic functions for instance the helpful relationship between two values. Specifically, it replaces ^ }} ^ }} line demolition with polynomial base ^ 9 }} ^ 9 }}, e.g. . } [1, x, x ^ , \ ledets, x ^ ]} } [1, x, x ^ , \ lddota, x ^ ]}. the answer to polynomial bases is that basic functions unit “not local”, which suggests that the input y worth of a given worth x = x0 is very obsessed on x-rated data values ​​x x0. [5] In fashionable calculations, polynomial base-functions unit used in conjunction with new basic functions, like splines, radial base functions, and wavelengths. These basic operating families provide the minimum equity for several data varieties.




Learn Advanced Apache Spark Certification Training Course to Build Your Skills
Weekday / Weekend BatchesSee Batch Details

The goal of polynomial regression is to model non-linear relationships between freelance and dependent variables (technically, between freelance variations and conjointly the conditional definition of dependent variables). this is {often|This can be} often reasonably just like the data point regression principle, that’s meant to capture non-linear regression relationships. Therefore, non-parameter retraction ways that like smoothing are additionally completely different useful ways that of polynomial retraction. variety of those ways that use a neighbourhood reasonably classical polynomial regression. The advantage of a typical polynomial retreat is that the lower recessive frame can typically be used (this in addition holds once completely different basic operate families like splines) unit used




Another last resort is to use kernelized models like support vector regression with a polynomial kernel. If the fossils have unequal variations, a little sq. scale is additionally accustomed to account for that.

Procedure to Apply Polynomial Regression:

Please find the steps below or the procedure for applying polynomial retrieval to any database:

Step 1: Import the appropriate database into any field (R or Python) and install the required packages to use the model.

Step 2: Divide the database into training and testing sets so that we can use the algorithm in the training data set and test it using the test data set.

Step 3: Use Test Data Analysis Methods to learn background data such as description, median, mode, first quartile, second quartile, etc.

Step 4: Use the line algorithm to go back to the database and read the model.

Step 5: Use the Polynomial regression algorithm in the database and read the model to compare the results into a RMSE or R square between lineback and polynomial regression.

Step 6: Visualise and predict both linear and polynomial regression results and identify which model predicts the database for best results.

Why polynomial Regression:

This is one of the regression methods used by experts to predict the outcome. It is defined as the relationship between independent and dependent variables where dependent variables are related to independent variations with the degree of nth. It does not require a relationship between dependent and independent variations to be linear, so if the line turns, you may have any polynomial name.




The main difference between linear regression and polynomial is that linear regulation requires independent variable dependencies to be linearly related, while this may be better aligned with the line if we add any higher level to the independent variable term in the equation. The polynomial regression equation with nth degree can be written as follows:




Y = b0 + a1x + a2x ^ 2 + a3x ^ 3 +…. if ^ n If we add high degrees like quadratic, then it turns the line into a curve that fits better with the data. Typically, it is used when points in a set of scattered data and a line model cannot explain the result clearly. We should always consider Overfitting and Underfitting while considering these qualifications in the equation.




It is best to consider a degree that exceeds all data points but sometimes taking high marks such as 10 or 20 may exceed all data points and minimize error but also catch the data passing the model and can be avoided by adding additional samples to the training data set. Therefore, it is always best to choose the right level to fit the model.




There are two methods used to determine the level of equation:

Advanced Choice: It is a way to extend a degree until it is important enough to define a model.

Backward Choice: It is a way to reduce the degree until it is important enough to define a model.

Uses of Polynomial Regression:

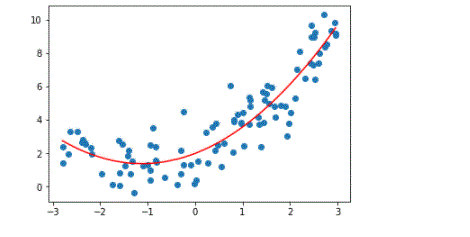
• It is utilised in several testing processes to provide a result of victimisation of this calculation.
• It provides an extremely outlined relationship between freelance and dependent variables.
• It is accustomed to study the isotopes of the sediments.
• It is accustomed to study the prevalence of varied diseases in any population.
• It is accustomed to study the generation of any synthesis.

What is polynomial regression in machine learning?

Like many other devices in machine learning, polynomial retardation as a theory comes from statistics. Statistics use it to analyse where there is a non-linear relationship between the value xx and the corresponding meaning with the terms yy.




Imagine if you wanted to predict how many of your new social media posts will be available any time after the publication. There is no linear relationship between the number of favourites and the past tense. Your new post will likely gain a lot of popularity within the first 24 hours after it is published, and then your popularity will decline.




Polynomial retardation is helpful in most cases. Since the relationship between independent and dependent variants does not need to be intertwined, you gain more freedom in choosing databases and the conditions with which you can work. This method can therefore be used when simple line deceleration is less than data.

Benefits of polynomial Regression:

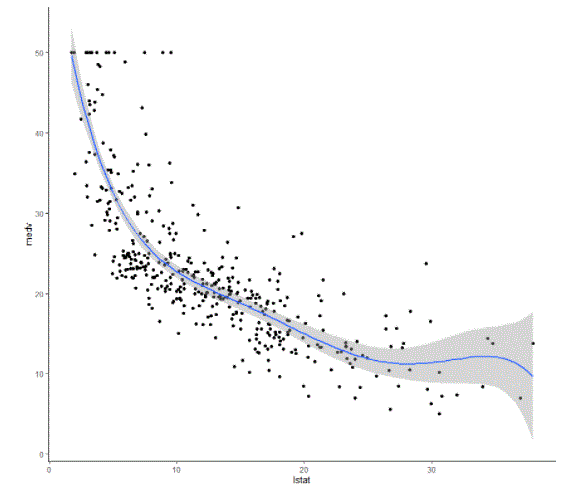
• A wide variety of activities is equally below.
• Polynomials are largely capable of a good variety of curvature.
• Polynomial provides the most effective balance of relationships between dependent and freelance variations.
• Disadvantages of exploitation Polynomial Regression
• This area unit is terribly sensitive to outsiders.
• The presence of 1 or 2 knowledge suppliers could considerably have an effect on the results of the non-linear analysis.
• In addition, sadly there are unit tools to confirm fewer models to search out outsiders in a non-line reversal than line reversal.

Conclusion:

Polynomial Regression is used in many organisations when they detect indirect relationships between independent and dependent variables. It is one of the hardest methods of regression compared to other methods of regression, so having in-depth knowledge of the method and algorithm will help you achieve better results.