
- Introduction to Search Strategies in AI
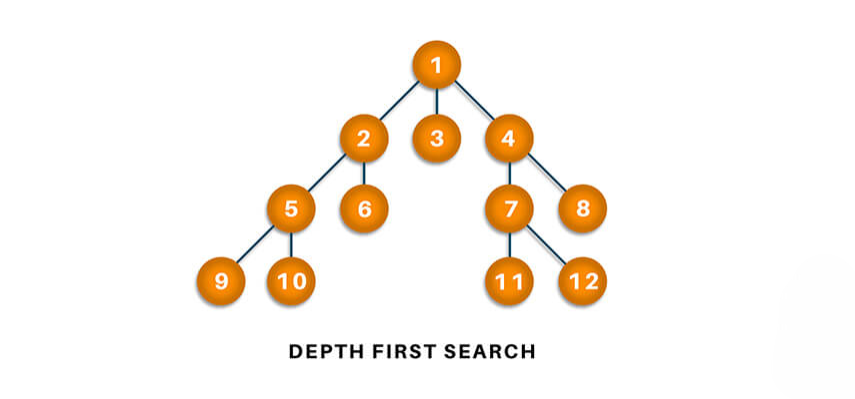
- Definition of Depth-First Search (DFS)
- Time and Space Complexity of DFS
- Applications of DFS in AI and Graph Theory
- Advantages and Disadvantages of DFS
- Implementation of DFS in Python
- Real-World Use Cases of DFS in AI
- Challenges in Using DFS for AI Problems
- Conclusion
Introduction to Search Strategies in AI
Search strategies are essential artificial intelligence (AI) tools for exploring and navigating vast problem spaces to identify solutions or optimize outcomes. These strategies are applied in various domains, such as pathfinding, game-playing, optimization, and general problem-solving. Search algorithms can be broadly classified into uninformed (or blind) and informed (or heuristic) searches. Uninformed search algorithms operate without domain-specific knowledge, exploring the search space systematically until a solution is found. Data Science Course Training algorithms are simple but inefficient, especially for large or complex problems. One of the most commonly used uninformed search algorithms is Depth-First Search (DFS). DFS explores along a branch before backtracking as far as possible, making it useful in scenarios where memory is limited. However, DFS can suffer from getting stuck in deep or infinite branches, making it less suitable for finding the shortest path or optimal solution. In contrast, informed search algorithms use heuristic information or domain-specific knowledge to guide the search process, making them more efficient in finding solutions quickly. Examples include A* and Greedy BFS . Informed search strategies are beneficial when the search space is ample, and a more targeted approach is needed to reach an optimal or near-optimal solution. Both uninformed and informed search techniques are crucial for AI systems to solve AI Problems efficiently.
Definition of Depth-First Search (DFS)
Depth-first search (DFS) is a graph traversal DFS Algorithm that explores a graph or tree starting from a root node and explores each branch as far as possible before backtracking. In other words, Agents in Artificial Intelligence explores a path to its most profound level before trying other potential paths. This strategy can be implemented using recursion or an explicit stack.DFS can be implemented using either artificial intelligence function or an explicit stack to keep track of the nodes to be explored.
Working on the DFS Algorithm
- Starting Point: The algorithm starts at a chosen node, typically the tree’s root or the graph’s starting state.
- Exploration: DFS explores the node and then recursively (or iteratively) visits its neighbors.
- Backtracking: Once DFS reaches a leaf node or a node with no unvisited neighbors, it backtracks to the most recent node with unexplored neighbors.
- Termination: The algorithm continues this process until it has explored all nodes in the graph or tree or finds the solution (if it exists).
Advance your Data Science career by joining this Data Science Online Course now.
Recursive vs. Iterative DFS
- Recursive DFS: This is the more natural and intuitive implementation of DFS. Each recursive call handles one level of depth, and the system’s call stack implicitly manages the backtracking process. The main advantage of recursion is that it is easier to implement and understand.
- Example (Recursive DFS):
- def dfs_recursive(graph, node, visited):
- visited.add(node)
- print(node)
- for neighbor in graph[node]:
- if neighbor not in visited:
- dfs_recursive(graph, neighbor, visited)
- Iterative DFS: This version uses an explicit stack to keep track of the nodes to visit. It is more suitable for large graphs where the recursion depth might exceed the system’s call stack limit. In iterative DFS in Python , we manually manage the stack and backtracking process.
- Example (Iterative DFS):
- def dfs_iterative(graph, start):
- visited = set()
- stack = [start]
- while stack:
- Node = stack.pop()
- if node not in visited:
- visited.add(node)
- print(node)
- stack.extend(graph[node] – visited)
- Time Complexity: The time complexity of DFS is O(V+E)O(V + E), where VV is the number of vertices (nodes) and EE is the number of edges in the graph. This is because each node is visited once, and each edge is explored once.
- Space Complexity: The space complexity depends on the implementation:
- Advantages: Simple and Easy to Implement DFS is intuitive and can be implemented with either recursion or an explicit stack. Space Efficiency DFS generally uses less memory than BFS, especially for deep graphs with a small number of nodes at each level. Can be More Suitable for Certain Problems: DFS in Python helps explore paths or find connected components in a graph, and it works well in scenarios where the goal is deep within the graph.
- Disadvantages: Not Optimal for Shortest Path: DFS does not guarantee finding the shortest path between two nodes (unlike BFS). May Get Stuck in Infinite Loops If a graph contains cycles, Data Science Course Training may revisit the same nodes endlessly unless cycle detection is implemented. Can Have High Space Complexity in Deep Graphs In cases of deep recursion or large trees, DFS in AI can require a significant amount of memory, particularly in the artificial intelligence (due to the system’s call stack).
- Pathfinding: Although DFS is not guaranteed to find the shortest path, it helps explore all possible paths in specific scenarios.
- Topological Sorting: In directed acyclic graphs (DAGs), Data Reduction in Data Mining is used to order tasks or dependencies for topological sorting.
- Solving Mazes: DFS is effective for solving maze problems, where it explores all potential paths.
- Cycle Detection: DFS can detect cycles in a graph, which is helpful in tasks like dependency resolution.
- Component Detection: DFS finds all connected components in an undirected graph.
- def dfs_recursive(graph, node, visited):
- visited.add(node)
- print(node)
- for neighbor in graph[node]:
- if neighbor not in visited:
- dfs_recursive(graph, neighbor, visited)
- def dfs_iterative(graph, start):
- visited = set()
- stack = [start]
- while stack:
- Node = stack.pop()
- if node not in visited:
- visited.add(node)
- print(node)
- stack.extend(graph[node] – visited)
- Puzzle Solving: DFS can explore all possible puzzle Mastering Python (e.g., the 8-puzzle problem) to find a solution.
- Web Crawling: DFS is helpful for web crawlers who need to examine the depth of links in a website, visiting as many pages as possible in depth-first order.
- Game Tree Search: In AI game playing (e.g., chess or tic-tac-toe), DFS is often used to explore all possible game moves (though DFS Algorithm like Minimax are more common for decision-making).
- State-Space Exploration: DFS explores different states in state-space problems, such as planning and scheduling tasks.
- Memory Consumption: DFS can consume a lot of memory in deep search spaces, especially in recursive implementations.
- Non-optimality: DFS may fail to find the optimal solution, especially in the case of pathfinding problems where the shortest path is required.
- Cycle Handling: The Functions of Statistics can get stuck in cycles unless proper cycle detection or visited node tracking is used, which can complicate the implementation..
- Depth Limitation: In cases of very deep graphs, DFS might not be feasible due to system limitations (e.g., stack overflow in recursive deployments).
Time and Space Complexity of DFS
In the case of recursive DFS, the space complexity is O(h)O(h), where hh is the maximum depth of the recursion tree (in the worst case, h=Vh = V, leading to O(V)O(V) space complexity). In the case of iterative DFS, the space complexity is O(V)O(V) due to the explicit stack used to store the nodes to be explored.
Learn the fundamentals of Data Science with this Data Science Online Course .
Advantages and Disadvantages of DFS
Take charge of your Data Science career by enrolling in ACTE’s Data Science Master Program Training Course today!
Applications of DFS in AI and Graph Theory
DFS is helpful in many AI and graph theory applications:
Implementation of DFS in Python
Here’s a simple implementation of DFS in Python using both recursive and iterative approaches:
Recursive DFS:
Iterative DFS:
Real-World Use Cases of DFS in AI
Want to ace your Data Science interview? Read our blog on Data Science Interview Questions and Answers now!
Challenges in Using DFS for AI Problems
Conclusion
Depth-First Search (DFS) is a fundamental search strategy used in AI and graph theory to explore graphs or trees. It starts at a root node and explores as far down a branch as possible before backtracking. Data Science Course Training approach is simple to implement and has low memory requirements, as it only needs to store the current path in memory, making artificial intelligence more efficient in terms of space compared to other strategies like Breadth-First Search (BFS). One of the advantages of DFS in AI is its ability to explore all possible paths or configurations, making it useful in problems where every possibility must be checked, such as puzzle-solving or combinatorial search problems. Additionally, DFS is relatively easy to implement using recursion or an explicit stack. However, DFS also has notable drawbacks. It does not guarantee finding the optimal solution, as it may explore long, inefficient paths before reaching the goal. In deep or cyclic graphs, DFS can also get stuck in infinite loops or take an impractically long time to find a solution. This makes it unsuitable for scenarios where optimality or efficiency is critical. In cases where finding the shortest or most optimal path is necessary, other search strategies, such as BFS or A*are often preferred. These methods ensure that the search progresses more systematically or intelligently, making them better suited for specific AI Problems Nonetheless, DFS remains a valuable tool for problems requiring exhaustive exploration.





