
- Introduction to Linear Discriminant Analysis
- How LDA Works in Dimensionality Reduction
- LDA for Classification Problems
- Advantages of LDA in Machine Learning
- Step-by-Step Implementation of LDA in Python
- Applications of LDA in AI and ML
- LDA in Natural Language Processing
- Future Developments in LDA Research
Introduction to Linear Discriminant Analysis (LDA)
Linear Discriminant Analysis (LDA) is a supervised machine learning method primarily used for classification tasks and dimensionality reduction. It aims to identify the linear combinations of input features that best separate different classes within the dataset. By projecting the original high-dimensional data onto a lower-dimensional space, LDA enhances the class discriminability, making it easier to distinguish between categories. This technique not only simplifies the dataset by reducing the number of features but also preserves the information that is most relevant for differentiating between the classes, a concept often emphasized in Data Science Training. As a result, it often improves the performance of classification algorithms by focusing on the most informative aspects of the data. LDA assumes that each class follows a Gaussian distribution and shares the same covariance matrix, which helps in estimating the optimal boundaries between categories. Commonly applied in areas such as facial recognition, text classification, and medical diagnosis, LDA is a powerful tool for improving both computational efficiency and classification accuracy, especially in scenarios involving multiple classes and high-dimensional data.
To Earn Your Data Science Certification, Gain Insights From Leading Data Science Experts And Advance Your Career With ACTE’s Data Science Course Training Today!
How LDA Works in Dimensionality Reduction
In LDA, dimensionality reduction occurs by projecting the data onto a lower-dimensional subspace while preserving the class separability. This is done by:
- Computing the scatter matrices: Calculate the within-class and between-class scatter matrices based on the data.
- Eigenvalues and Eigenvectors: Solve for the eigenvalues and eigenvectors of the matrix SW−1SBS_W^{-1} S_B. These eigenvectors form the new axes that maximize the class separability.
- Projection: Project the original data onto these eigenvectors for a lower-dimensional representation, similar to how Excel Power Query transforms and simplifies complex datasets for easier analysis.
- Choosing the number of components: To reduce the data to a specific number of dimensions, select the top eigenvectors corresponding to the largest eigenvalues. The number of components is typically chosen based on the desired dimensionality of the projected space.
- Dimensionality Reduction: By retaining only the most significant eigenvectors, LDA effectively reduces the feature space while maintaining the critical information needed for classification.
- Class-wise Mean Computation: For each class, compute the mean vector, which represents the centroid of that class in the feature space. These mean vectors are essential for constructing the between-class scatter matrix.
- Optimization of Class Separation: LDA focuses on maximizing the ratio of between-class variance to within-class variance, ensuring that the data is projected onto a subspace that enhances class separability.
- Train LDA: Use the training data to compute class means, within-class scatter matrix (SWS_WSW), and between-class scatter matrix (SBS_BSB). The class represents the average of the feature vectors for each class, while the scatter matrices capture the spread of data within each class and between classes.
- Project Data: Once the scatter matrices and eigenvectors are computed, project the original data points onto the eigenvectors corresponding to the largest eigenvalues. This step reduces the dimensionality of the data while maximizing the class separability, making it easier for a classifier to distinguish between classes.
- Classify: Apply a linear classifier, such as a linear discriminant, to classify the data based on the newly reduced features a process that can be complemented by feature selection techniques like the Chi-Square Test. Since LDA projects the data onto a space that best separates the classes, it can enhance the performance of linear classifiers like Logistic Regression or Support Vector Machines (SVM).
- Evaluate Performance: After classification, evaluate the model’s performance using metrics such as accuracy, precision, recall, and F1-score. This step ensures that the dimensionality reduction performed by LDA does not compromise the model’s ability to correctly classify the data.
- Cross-Validation: Perform cross-validation to assess the generalization ability of the LDA model. By splitting the dataset into multiple training and validation sets, cross-validation helps ensure that the classifier’s performance is not overfit to a particular subset of the data.
- Visualize the Results: For datasets with more than two features, visualize the results of LDA by plotting the data points in the lower-dimensional space. This helps in understanding how well the classes are separated and can provide insights into the effectiveness of the dimensionality reduction.
- Tuning Hyperparameters: If necessary, tune the hyperparameters of the classifier or the LDA procedure to optimize performance. For instance, you might experiment with different numbers of components to find the optimal balance between reducing dimensionality and preserving class separability.
- from sklearn.discriminant_analysis import LinearDiscriminantAnalysis
- from sklearn.datasets import load_iris
- from sklearn.model_selection import train_test_split
- from sklearn.preprocessing import StandardScaler
- from sklearn.metrics import accuracy_score
- data = load_iris()
- X = data.data
- y = data.target
- X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.3, random_state=42)
- scaler = StandardScaler()
- X_train = scaler.fit_transform(X_train)
- X_test = scaler.transform(X_test)
- lda = LinearDiscriminantAnalysis(n_components=2)
- X_train_lda = lda.fit_transform(X_train, y_train)
- lda_classifier = LinearDiscriminantAnalysis()
- lda_classifier.fit(X_train_lda, y_train)
- X_test_lda = lda.transform(X_test)
- y_pred = lda_classifier.predict(X_test_lda)
- print(“Accuracy:”, accuracy_score(y_test, y_pred))
- Face Recognition: LDA is used in facial recognition systems to reduce the dimensionality of image data while preserving class separability (individual faces).
- Medical Diagnosis: LDA is used to classify patient data into disease categories based on various features.
- Speech Recognition: LDA reduces the dimensionality of speech signals for classification tasks, a concept that contrasts with front-end tasks like Email Validation in JavaScript, which focus on ensuring correct input formats rather than feature extraction.
- Document Classification: In Natural Language Processing (NLP), LDA can classify text documents based on their content.
- Financial Fraud Detection: LDA is applied in the financial industry to detect fraudulent transactions by classifying customer behavior patterns into legitimate or suspicious categories.
- Customer Segmentation: In marketing and business analytics, LDA is used to segment customers based on their purchasing behaviors, demographic information, or product preferences.
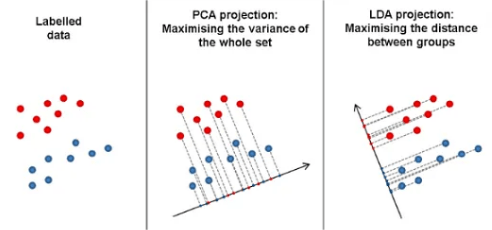
LDA for Classification Problems
LDA can classify data by projecting the data into a lower-dimensional space and then applying a classification algorithm (typically a linear classifier like a decision boundary). It works as follows:
Are You Interested in Learning More About Data Science? Sign Up For Our Data Science Course Training Today!
Advantages of LDA in Machine Learning
Linear Discriminant Analysis (LDA) offers several advantages in machine learning, particularly for classification and dimensionality reduction tasks. One of its key benefits is its ability to reduce the dimensionality of high-dimensional datasets while preserving class separability. This results in more efficient processing, reducing computational complexity and memory requirements, which is a key focus in Data Science Training. By projecting the data onto a lower-dimensional space, LDA simplifies the dataset without losing critical information, improving the performance of machine learning algorithms, especially when working with limited training data. Another significant advantage of LDA is that it can handle both binary and multi-class classification problems effectively.
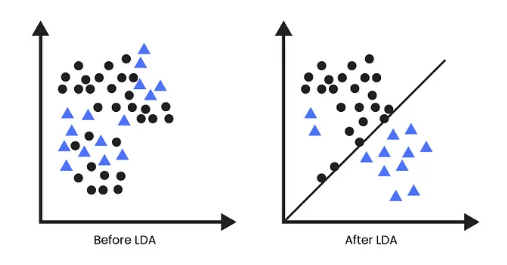
It assumes that the data from each class follows a Gaussian distribution with a shared covariance matrix, making it robust and effective in many real-world scenarios. LDA also works well when the classes are well-separated, leading to high accuracy in classification tasks. Additionally, LDA is relatively simple and interpretable, allowing practitioners to easily understand the resulting projections and decision boundaries. It is particularly useful in applications like facial recognition, medical diagnostics, and text classification, where class separability is crucial for effective classification.
Step-by-Step Implementation of LDA in Python
K-Nearest Neighbors Here is an example of implementing LDA for dimensionality reduction and classification using Python and scikit-learn:
Import necessary libraries
Load dataset
Split data into training and testing sets
Standardize the data
Initialize and fit LDA
Reduce to 2 dimensions
Train classifier
Project test data into LDA space
Make predictions
Evaluate accuracy
Want to Pursue a Data Science Master’s Degree? Enroll For Data Science Masters Course Today!
Applications of LDA in AI and ML
LDA has several applications in machine learning and artificial intelligence:
LDA in Natural Language Processing
In Natural Language Processing (NLP), LDA (Latent Dirichlet Allocation) is commonly used for topic modeling, a technique for discovering the underlying thematic structure within a large corpus of text. Unlike Linear Discriminant Analysis (also referred to as LDA), which is a supervised learning method used for classification and dimensionality reduction, Latent Dirichlet Allocation is an unsupervised learning technique. LDA in topic modeling works by grouping words that frequently appear together, allowing the identification of topics based on word co-occurrence patterns quite different from tasks like building a Calculator Using JavaScript, which focuses on numerical computation and UI interaction. This process helps categorize extensive collections of documents into distinct topics, making it easier to analyze and interpret large amounts of text data. By modeling the distribution of words and topics, LDA allows for automatic extraction of themes from documents, which can be applied in areas like document clustering, content recommendation, and information retrieval. Despite sharing the same acronym, LDA in NLP for topic modeling is fundamentally different from Linear Discriminant Analysis used in classification tasks.
Are You Preparing for Data Science Jobs? Check Out ACTE’s Data Science Interview Questions & Answer to Boost Your Preparation!
Future Developments in LDA Research
Future developments in Linear Discriminant Analysis (LDA) research are likely to focus on enhancing its applicability and performance across various domains. One key area of research is improving LDA’s scalability to handle high-dimensional data more efficiently, especially in the context of large datasets commonly found in fields like genomics, image processing, and social media analysis. This could involve developing more advanced dimensionality reduction techniques or hybrid models that integrate LDA with other algorithms such as deep learning or ensemble methods. Another promising direction is robustness to non-Gaussian distributions. Traditional LDA assumes that data from each class follows a Gaussian distribution with a shared covariance matrix, but real-world data often deviates from this assumption a challenge frequently discussed in Data Science Training. Researchers may focus on creating more flexible versions of LDA that can handle non-Gaussian distributions and heterogeneous data. Additionally, semi-supervised learning approaches for LDA could be explored, where limited labeled data is combined with a large amount of unlabeled data to improve model performance, particularly in situations where labeling is expensive or time-consuming. Finally, there is potential for LDA to be integrated with other dimensionality reduction techniques, such as t-SNE or UMAP, to create hybrid methods that can preserve class separability while better capturing complex data structures. This would enhance LDA’s effectiveness in modern machine learning tasks, including image recognition, natural language processing, and financial analysis.



