
- A Chi-Square Test: What Is It?
- The Chi-Square Test Formula
- Chi-Square Test Types
- How to Conduct a Chi-Square Analysis
- When Is the Chi-Square Test Appropriate to Use?
- The Chi-Square Test’s Characteristics
- The Chi-Square Test’s Drawbacks
- Conclusion
A Chi-Square Test: What Is It?
The Chi-Square (χ²) test is a fundamental statistical method used to evaluate whether there is a significant difference between observed and expected frequencies within categorical data. It plays a key role in determining relationships between two categorical variables or assessing how well the observed distribution aligns with a theoretical or expected distribution. As a non-parametric test, the Chi-Square test does not assume a normal distribution of data, making it especially useful when working with qualitative or grouped data. There are three main types of Chi-Square tests commonly covered in Data Science Training the goodness of fit test, which examines whether a sample distribution fits an expected distribution; the test of independence, which evaluates whether two categorical variables are related; and the test for homogeneity, which compares the distribution of a variable across multiple groups. The Chi-Square test is widely used across various disciplines, including social sciences, marketing, public health, education, and biology. It is particularly valuable in survey analysis, population studies, and experiments involving group comparisons. While highly versatile, proper application requires meeting certain assumptions, such as having adequate sample size and expected cell counts, to ensure valid and reliable results.
To Earn Your Data Science Certification, Gain Insights From Leading Data Science Experts And Advance Your Career With ACTE’s Data Science Course Training Today!
The Chi-Square Test Formula
The formula for the Chi-Square test is used to compute a test statistic (χ²) that compares the observed frequencies (actual data) to the expected frequencies (predicted or hypothesized data). The formula is as follows: <χ2=∑(Oi−Ei)2Ei\chi^2 = \sum \frac{(O_i - E_i)^2}{E_i}> In the Chi-Square (χ²) test formula, Oi represents the observed frequency for the i-th category, and Ei represents the expected frequency for that same category. The formula involves calculating the squared difference between observed and expected frequencies, dividing this value by the expected frequency, and then summing the results across all categories an essential concept discussed in Why Data Science Matters & How It Powers Business Value. This summation gives the Chi-Square statistic, which measures how much the observed data deviates from what was expected under the null hypothesis.
A larger value indicates a greater difference between observed and expected frequencies, suggesting a potential significant relationship or deviation. Once the Chi-Square value is calculated, it is compared to a critical value from the Chi-Square distribution table, based on the degrees of freedom and the chosen significance level. This comparison determines whether the null hypothesis should be rejected or not.
Chi-Square Test Types
Chi-Square Goodness of Fit Test
This test determines whether a sample data matches an expected distribution. It checks if the observed data follows a specific distribution you hypothesize about (such as a uniform distribution, normal distribution, etc.).
- Example: You might roll a die 60 times and want to check if each number appears with equal frequency (a fair die). You would compare the observed frequencies with the expected frequencies (which should be 10 for each face of the die if the die is fair).
- Example: A study on smoking behavior might look at whether there is a relationship between gender (male/female) and smoking status (smoker/non-smoker), as illustrated in Top Data Science Books for Beginners & Advanced Data Scientist. The test of independence would help determine if the smoking status of a person is independent of their gender.
- Example: A market research company might want to check if customer preferences for a product are the same across different geographical regions (North, South, East, West). The Chi-Square Test of Homogeneity can assess if there is a difference in preferences across these regions.
- Null Hypothesis (H0H_0): No significant difference exists between the observed and expected frequencies (i.e., the variables are independent, or the data follows the expected distribution).
- Alternative Hypothesis (H1H_1): A significant difference exists between the observed and expected frequencies (i.e., the variables are dependent, or the data does not follow the expected distribution).
- For the Goodness of Fit Test, which is often taught in Data Science Training, df=k−1, where k is the number of categories.
- For the Test of Independence or Homogeneity, df=(r−1)(c−1)df = (r – 1)(c – 1), where rr is the number of rows and cc is the number of columns in the contingency table.
- If the calculated Chi-Square statistic is larger than the critical value, reject the null hypothesis. This indicates a significant difference or association between the observed and expected frequencies.
- If the calculated Chi-Square statistic is smaller than the critical value, it fails to reject the null hypothesis. This suggests no significant difference exists between the observed and expected frequencies.
- Non-parametric: The Chi-Square test does not require any assumptions about the data distribution.
- Based on Frequencies: It compares observed frequencies with expected frequencies rather than working with means or variances.
- Sensitivity to Sample Size: Larger sample sizes tend to make the Chi-Square test more sensitive to slight differences, which may detect significant differences even when they are not practically meaningful.
- Asymptotic: The Chi-Square test works well with large samples. However, the results may not be reliable for small samples, a limitation often discussed in Data Mining Vs. Machine Learning.
- Categorical Data Requirement: The Chi-Square test is specifically designed for categorical variables, meaning the data must be in the form of counts or frequencies within distinct categories.
- Independence of Observations: Each observation in the dataset must be independent of the others. Violating this assumption can lead to inaccurate results.
- Degrees of Freedom: The outcome of the Chi-Square test depends on the degrees of freedom, which are based on the number of categories or variables involved. This affects the critical value used for hypothesis testing.
- Directional Limitation: The Chi-Square test can tell whether there is a significant difference or association, but it does not indicate the direction or strength of the relationship between variables.
- Requires Large Sample Sizes: For the test to be valid, the expected frequency for each category must be at least 5. The Chi-Square test may not be applicable for small datasets, and other tests (such as Fisher’s Exact Test) might be more appropriate.
- Sensitive to Small Frequencies: The Chi-Square test is unreliable when categories have minor expected frequencies. If the expected frequency is too low, the test statistic might be inflated, leading to inaccurate conclusions.
- Does Not Indicate the Strength of the Relationship: While the Chi-Square test can tell you whether an association exists between variables, it does not provide any information about the strength or direction of the relationship.
- Does Not Handle Continuous Variables: The Chi-Square test is unsuitable for continuous data. It is designed explicitly for categorical data, a distinction that is important when comparing Machine Learning Vs Deep Learning.
- Affected by Sample Distribution: The test assumes that the sample is randomly drawn and representative of the population. Non-random sampling can lead to biased or misleading results.
- Only Detects Association, Not Causation: Even if a significant association is found, the Chi-Square test cannot determine whether one variable causes changes in another; it only shows correlation, not causation.
- Requires Mutually Exclusive Categories: The categories being analyzed must be clearly defined and mutually exclusive, meaning each observation can belong to only one category. Overlapping or ambiguous categories can invalidate the results.
Chi-Square Test of Independence
This test determines if there is a significant association between two categorical variables. It is most often used in contingency tables to assess whether one variable’s distribution is independent of another variable’s distribution.
Chi-square test of Homogeneity
This test compares the distribution of a categorical variable across different populations or groups. It checks whether other groups or populations have the same distribution for a particular categorical variable.
Interested in Learning More About Data Science? Sign Up For Our Data Science Course Training Today!
How to Conduct a Chi-Square Analysis
Step 1: State the Hypotheses
Step 2: Set the Significance Level (α\alpha)
Typically, α\alpha is set at 0.05, representing a 5% probability of making a Type I error (rejecting a true null hypothesis).
Step 3: Calculate the Chi-Square Statistic
Use the Chi-Square formula to calculate the test statistic: <χ2=∑(Oi−Ei)2Ei\chi^2 = \sum \frac{(O_i - E_i)^2}{E_i}> OiO_i is the observed frequency, and EiE_i is the expected frequency for each category.
Step 4: Determine the Degrees of Freedom (df)
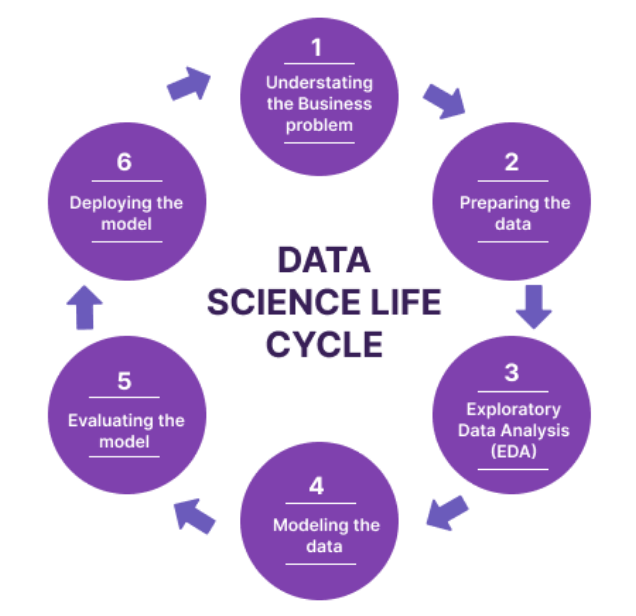
Step 5: Compare the Calculated Chi-Square Value to the Critical Value
Find the critical value from the Chi-Square distribution table using the degrees of freedom and the chosen significance level. You reject the null hypothesis if the calculated Chi-Square statistic exceeds the critical value.
Step 6: Make a Decision
When Is the Chi-Square Test Appropriate to Use?
The Chi-Square test for categorical data is appropriate to use when you are working with categorical variables and want to determine whether there is a significant association between variables or whether observed frequencies differ from expected ones. It is most commonly applied in three situations: testing goodness of fit, independence, and homogeneity. The goodness of fit test is used when you want to see if a sample distribution matches an expected theoretical distribution. The test of independence helps determine whether two categorical variables are related or independent within a population. The test for homogeneity is used to compare the distribution of a categorical variable across different groups or populations, highlighting concepts covered in The Importance of Machine Learning for Data Scientists. The Chi-Square test for categorical data is suitable when the data consists of counts or frequencies, not percentages or continuous values. It also assumes that the observations are independent and that the expected frequency in each category is at least 5 for valid results. This test is widely used in data analysis in social sciences, marketing, biology, public health, and education to analyze survey responses, experimental data, and population trends. When these conditions are met, the Chi-Square test provides a reliable and straightforward method for statistical analysis in research and making meaningful inferences.
Considering Pursuing a Master’s Degree in Data Science? Enroll in the Data Science Masters Course Today!
The Chi-Square Test’s Characteristics
The Chi-Square Test’s Drawbacks
Preparing for Data Science Job Interviews? Have a Look at Our Blog on Data Science Interview Questions & Answer To Ace Your Interview!
Conclusion
The Chi-Square test is a widely used statistical method for analyzing categorical data. It serves several key purposes, including testing the goodness of fit, evaluating the independence of variables, and assessing the homogeneity of distributions across different groups. By comparing observed frequencies in a dataset to the expected frequencies under a specific hypothesis, researchers can determine whether any significant differences exist. This helps in drawing conclusions about relationships between variables or how well observed data matches theoretical models. The Chi-Square test is especially valuable in fields like social sciences, healthcare, education, and market research, and is a key component of Data Science Training, where understanding patterns in categorical data is crucial. However, for the test to yield accurate results, certain assumptions must be met. These include having a sufficiently large sample size, ensuring that data is drawn from independent observations, and avoiding expected frequencies that are too small (typically less than five). While powerful, the Chi-Square test has its limitations and should be applied with care. When used appropriately, it becomes a reliable tool for uncovering meaningful insights and supporting evidence-based decision-making across various disciplines.





