Last updated on 13th May 2025| 8337
(5.0) | 19876 Ratings
E-mail this post
- Introduction to Linear Regression in Python
- Understanding Linear Regression
- What is the Best Fit Line?
- Evaluation Metrics for Linear Regression
- Types of Linear Regression
- Python Implementation of Linear Regression
- Applications of Linear Regression
- Advantages and Disadvantages of Linear Regression
- Conclusion
Introduction to Linear Regression in Python
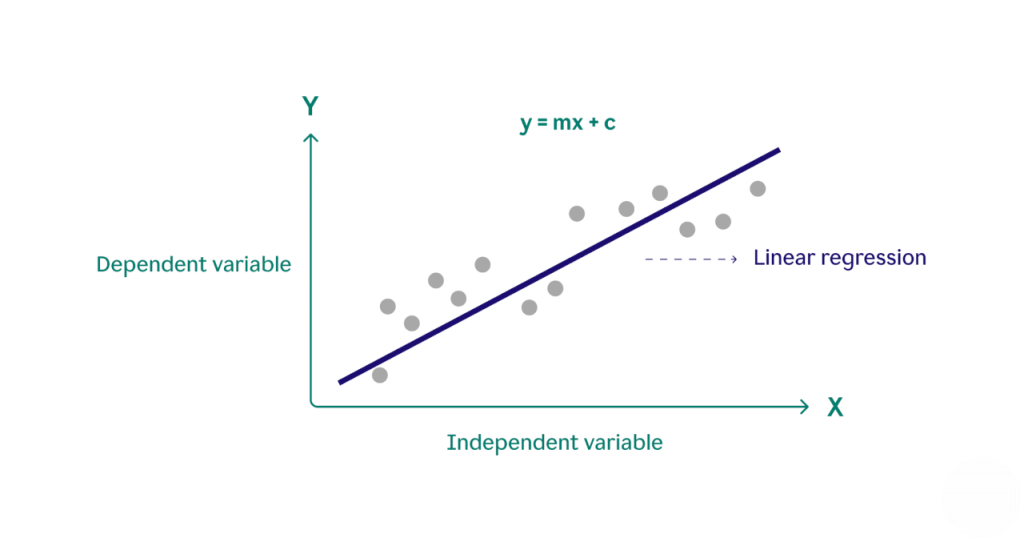
Linear Regression in Python is a predictive modeling technique. It is used whenever there is a linear relation among the structured and impartial variables. It is used to estimate precisely how many “y” will alternate when “x” adjusts a positive amount. In easy linear Regression, there’s the handiest unbiased variable, and the connection is modeled using a line of the shape y = mx + c, wherein m is the slope and c is the intercept. In a couple of linear regressions, multiple Regressio unbiased variables are used, and the equation extends to consist of a couple of terms. Linear Regression is broadly carried out in machine learning including economics, business, fitness sciences, and social sciences for predicting trends, studying risk, and making knowledgeable selections primarily based on data.
Understanding Linear Regression
Neo, a telecom network, desires to examine the connection between patron tenure and month-to-month prices. The shipping supervisor applied linear Regression, using tenure because of the impartial variable and month-to-month prices because of the structured variable. The consequences display a high-quality correlation longer tenure ends in better prices. The high-quality suit line facilitates the expectation of destiny prices primarily based on tenure. Similarly, if a patron’s tenure is sixty-nine months, with the assistance of the high-quality suit line, the shipping supervisor can expect that the patron`s month-to-month prices might be around $110.
Are You Interested in Learning More About Data Science? Sign Up For Our Data Science Course Training Today!
What is the Best Fit Line?
The line of high-quality suits is not anything; rather, it is the line that expresses the connection among the record points. Let us see how to discover the high-quality suit line in Linear Regression in Python. To discover the high-quality line, we use something called the residual sum of squares (RSS). In RSS, we take the rectangular residuals and sum them up. In an easy linear Regression line, if the coefficient of x is high quality, we will conclude that the connection among the impartial and structured variables is high quality. If the coefficient of x is negative, we will say that the connection among the impartial and structured variables is negative. Cost Function of Linear Regression In Linear Regression, the maximum generally used fee feature is Mean Squared Error (MSE).
To Explore Data Science in Depth, Check Out Our Comprehensive Data Science Course Training To Gain Insights From Our Experts!
Evaluation Metrics for Linear Regression
Evaluation metrics determine the quality of a statistical or system-mastering version. Key metrics encompass R-squared, Adjusted R-squared, MSE, RMSE, and MAE, which support verifying version accuracy and predictive performance.
- R-squared (R2): R2 measures the percentage of variance within the structured variable defined using the impartial variables. A fee towards 1 suggests a higher shape; at the same time as zero way, the version explains no variance. However, including greater variables can artificially boost R2.
- Adjusted R-squared: Unlike R2, Adjusted R-squared debts are used to calculate the number of predictors within the side version. Machine learning penalizes needless variables, making it more reliable for multiple Regression.
- MSE (Mean Squared Error): MSE calculates the common squared variations among real and anticipated values. A lower MSE results in higher version performance; however, it penalizes massive mistakes more than small ones.
- RMSE (Root Mean Squared Error): RMSE is the rectangular root of MSE, making it more interpretable as it’s miles within the identical unit because of the goal variable. Lower RMSE suggests a higher version.
- MAE (Mean Absolute Error): MAE measures common absolute distinction among the real and anticipated values. Unlike MSE, it treats all mistakes similarly and is much less sensitive to outliers.
Types of Linear Regression
Linear Regression may be classified into differing types based on the number of impartial variables and the character of the data.
- Simple Linear Regression: Simple linear Regression is beneficial for predicting and expert correlations among one impartial variable and one structured variable.
- Multiple Linear Regression: Multiple Regression is just like Regression analysis. However, it consists of numerous impartial fees, implying that we expect a fee primarily based on or greater variables.
- Polynomial Regression: Polynomial Regression is a form of multiple Regression Evaluation Metrics that uses the impartial variable`s higher-diploma functions, such as squares and cubes, to shape the data. It permits more problematic interactions among the variables than linear Regression.
Gain Your Master’s Certification in Data Science by Enrolling in Our Data Science Masters Course.
Python Implementation of Linear Regression
We`ll be studying the Boston Housing Price Dataset, which contains 506 entries and thirteen attributes, along with a goal column. Let’s take a brief look at this dataset.
- Crim: Crime fee consistent with per capita with the aid of using town
- Zn: Fraction of residential land allotted for massive plots (over 25,000 sq. ft.)
- Indus: Fraction of non-retail commercial enterprise acres in the town
- Chas: Indicator for a Charles River proximity (1 if close; zero if not)
- Nox: PPM (elements consistent with 10 million) awareness of nitrogen oxides
- Rm: The Typical wide variety of the rooms in a residence
- Age: Fraction of houses constructed earlier than 1940
- Dis: Average distance to 5 predominant Boston workplaces
- Rad: Proximity index to predominant highways
- Tax: Property tax fee (consistent with $10,000)
- Ptratio: Student-to-instructor ratio in town
- Black: Value calculated by 1000(Bk – zero.63)^2, in which Bk represents a fraction of Black citizens in town
- Lstat: Percentage of the populace with decreased status
- Medv: Median fee of houses (in $1000s)
Data Description
In this linear regression tutorial, our goal is to expand predictive fashions for housing prices.
Model Development: With our clean expertise in our dataset, let’s continue to assemble our linear multiple Regression fashions in Python.
Want to Learn About Data Science? Explore Our Data Science Interview Questions & Answer Featuring the Most Frequently Asked Questions in Job Interviews.
Applications of Linear Regression
Linear Regression is widely used in various domains for predictive Regression analysis and decision-making. Here are some key applications: Evaluating trends and sales estimates Businesses use linear Regression to examine past sales data and forecast future trends. By understanding how factors such as pricing, machine learning, promotions, and client demand affect sales, businesses may optimize inventories, marketing efforts, and revenue estimates. Market analysts use Linear Regression line to analyze consumer behavior, competitive pricing, and demand variations. It assists organizations in determining how variables such as advertising expenditure, economic conditions, and customer preferences affect product success in the market. Linear Regression is used in medicine to forecast disease development, patient recovery rates, and treatment results based on age, lifestyle, and medical history. It is also helpful in calculating healthcare expenses and optimizing resource allocation. Forecasting consumer spending Economists and businesses use Regression analysis to forecast consumer spending based on income, inflation, and interest rates. This aids in budgeting, price tactics, and financial planning to keep up with market demand.
Advantages and Disadvantages of Linear Regression
- Advantages of Linear Regression: Linear Regression is easy to understand and interpret, making it a great starting point for statistical modeling. It requires minimal computational power, making Best Fit Line ideal for large datasets. Linear Regression performs well if there is a linear relationship between the independent and dependent variables. Helps identify the impact of every independent variable on the dependent variable using coefficients. Frequently used in forecasting sales, trends, and other business metrics.
- Disadvantages of Linear Regression: Linear Regression assumes a Regression line relationship, which may not hold for complex, non-linear data. Outliers can significantly affect the regression line, leading to inaccurate predictions. When independent variables are highly correlated, Evaluation Metrics can distort coefficient estimates and reduce model reliability. It does not handle categorical data well unless properly encoded. With too many features, the model may fit the training data too well but perform poorly on new data.
Conclusion
In conclusion, Linear Regression is a fundamental and widely used algorithm in statistics and machine learning for modeling the relationship between a dependent variable and one or more independent variables. Best Fit Line is simple, interpretable, and efficient, making it a great starting point for predictive Regression analysis. Linear Regression provides insights into how variables are related and can help forecast trends and make data-driven decisions. However, it assumes a linear relationship, which may not always hold in real-world scenarios, and it can be sensitive to outliers and multicollinearity. Despite these limitations, when its assumptions are met, linear Regression is a powerful and valuable tool for understanding and predicting continuous outcomes.
