Skewness vs Kurtosis : Comparision and Differences | Which Should You Learn?

Last updated on 17th Dec 2021, Blog, General

(5.0) | 19483 Ratings 8853

Share:

Skewness is a measure of symmetry, or more precisely, the lack of symmetry. A distribution, or data set, is symmetric if it looks the same to the left and right of the center point. Kurtosis is a measure of whether the data are heavy-tailed or light-tailed relative to a normal distribution.

• Introduction to Skewness vs Kurtosis
• Comparison Chart
• Definitions
• Key Differences Between Skewness and Kurtosis
• Types of skewness & Excess Kurtosis
• Characteristics of Skewness
• Distributions
• Conclusion

Introduction to Skewness vs Kurtosis:

Tilt, in principle, means that you are not in the middle, and even in maths, it means a lack of balance. With the help of rowing, one can see the shape of the data distribution. Kurtosis, on the other hand, refers to the directness of the peak in the distribution curve. The main difference between skewness and kurtosis is that previous discussions of the level of equilibrium, and the latter deals with the level of skewness, in the distribution of frequency.




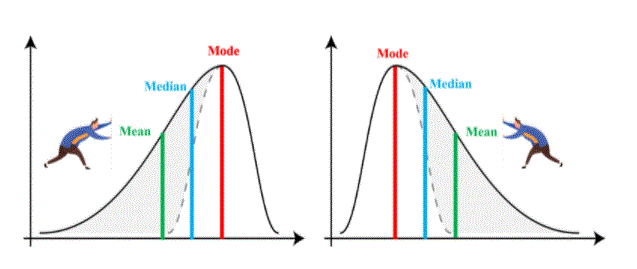
Data can still be distributed in many ways, such as multiple left or right distribution or even distribution. When data is evenly distributed in the central area, it is called Normal Distribution. It is perfectly aligned, a curved metal shape, i.e. both sides are equal, so it does not tilt. Here all three mean, median, and mode sleep at the same time.




Skewness and Kurtosis are two important distribution factors studied by descriptive statistics. To further our understanding of the two perspectives, let’s look at the article given below

Comparison Chart:

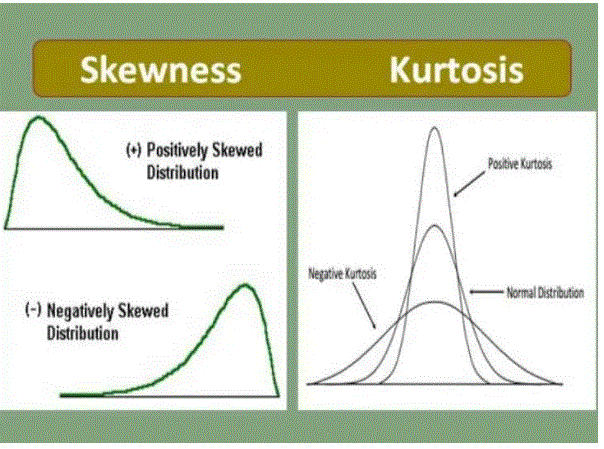
• Definition of meaning refers to the slope of the distribution that determines your equilibrium with the definition. Kurtosis refers to the degree of continuous sharpening of a curve, in the distribution of frequency.


• Rate Lopsided Degree in Distribution. Tail level in distribution.


• What’s going on? It is an indication of the lack of equity in the distribution of frequency. It is a data rate, which can be high or low in relation to general distribution.


• Represents the value and location of the skew.w.Long and how sharp is the middle peak?

Definitions:

Definition of Skewness

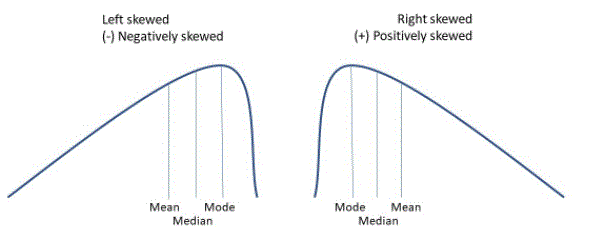
The term ‘skewness’ is used to denote a lack of balance in the definition of a database. It is a sign of deviation from the definition, being larger on one side than the other, i.e. a distribution attribute with one tail heavier than the other. Tilt is used to indicate the state of data distribution.




In a twisted distribution, the curve is extended to the left or right. Therefore, when the structure is extended to the upper right side, it means a good inclination, where the median means. On the other hand, when the building is extended upwards to the left, then it is called incorrect inclination, therefore, means median mode.




Definition of Kurtosis

In mathematics, kurtosis is defined as a parameter of the relative sharpness of the curvature of a possible distribution curve. Detects how visuals are integrated within the distribution area. It is used to indicate the flatness or height of a distribution curve and usually measures the tails with or without distribution.




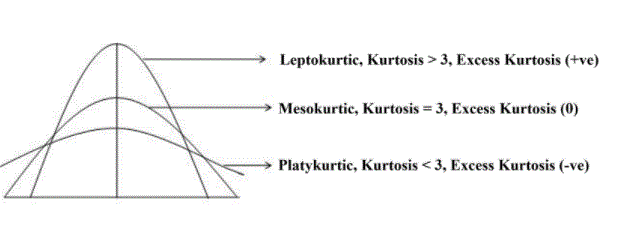
Direct kurtosis represents that the distribution is much higher than the normal distribution, while negative kurtosis shows that the distribution is slightly higher than the normal distribution. There are three types of distribution:

Leptokurtic: Highly elevated with fat tails, and low flexibility.

Mesokurtic: Medium peak

Platykurtic: The highest and most scattered area.

Key Differences Between Skewness and Kurtosis:

The element of distribution of a frequency that confirms its equality in terms of meaning is called a slope. Kurtosis, on the other hand, refers to the relative identification of a common metal curve, which is defined by the frequency distribution.




Tilt is a measure of the level of lopsidedness in the frequency response. In contrast, kurtosis is a measure of tailedness in the frequency range.




The slope is an indication of a lack of balance, i.e. both the left and right sides of the curve are uneven, relative to the centre. Contrary to this, kurtosis is a measure of high or flat data, in relation to the distribution of opportunities.




The slope shows how much the deviation is and in which direction it means? In contrast, does kurtosis define the length and sharpness of the central peak?

Learn Advanced Apache Spark Certification Training Course to Build Your Skills

Weekday / Weekend BatchesSee Batch Details

Types of skewness & Excess Kurtosis:

1. sensible is pointed or canted to the proper

Statistically, a well-distorted distribution could be a variety of distribution wherever, in contrast to equally distributed information wherever all average inclusions (i.e., media, and mode) area unit equal, with twisted information, the steps area unit spread, i.e. Well. Inverted Distribution could be a variety of distribution wherever the quantitative relation, median, and distribution mode area unit a lot of positive than zero or zero. In other words, the results are unit curvilinear at very cheap prices. the speed are going to be more than median as the median is that the price and therefore the mode remains the best value.




2. Evil inclined to the left

Negative twisted distribution could be a direct reversal of the twisting force. Within the calculations, the inaccurate curvilinear distribution refers to the distribution pattern wherever the multiple values ​​are within the right part of the graph, and therefore the distribution tail is unfolded on the left facet. By default, the definition of information is a smaller {amount} than the median (a large amount of information pushed to the left). Distorted Distribution could be a variety of distribution wherever definition, median, and distribution mode area unit negative instead of positive or zero.




3. Excessive Kurtosis

Excess kurtosis is employed in mathematical and chance analysis to check the kurtosis constant therewith of general distribution. Excess kurtosis is positive (Leptokurtic spread), negative (Platykurtic distribution), or on the point of egg (Mesokurtic distribution). Since traditional circulation has three kurtosis, further kurtosis is calculated by cathartic kurtosis by three.




Types of excessive kurtosis

• Leptokurtic or significant tail distribution (kurtosis is over traditional distribution).
• Mesokurtic (kurtosis is comparable to traditional distribution).
• Platykurtic or short-tail distribution (kurtosis is a smaller amount common than normal).
• Leptokurtic (kurtosis> 3)



Leptokurtic has terribly long and dense tails, which suggests it’s a lot to induce. The positive rates of kurtosis indicate that the distribution is high and has thick tails. Excessive positive kurtosis indicates a distribution wherever multiple numbers area units are found within the distribution lines rather than round the scale.

Characteristics of Skewness:

From the on top of definitions, the slanted options is also represented below:

• Specifies the spatiality of the mathematical sequence.
• State the distinction within the estimates i.e.. That is, Medi and Mode.
• Specify the gap distinction between the Quartiles, and also the Median.
• They are often smart, or they are often unhealthy. If there’s additional target lower costs it’s higher, and if there’s additional target higher costs it becomes negative.



Symptoms of Kurtosis:

Kurtosis may be a mathematical verb to describe the speed at which points meet within the tail or the very best rate of distribution. Height is the longest part of the unfold, and tails at the ends of the unfold. There are 3 forms of kurtosis: mesokurtic, leptokurtic, and platykurtic.




Kurtosis may be alive whether or not the info features a significant tailor, a light-weight tail in relevance Gaussian distribution. That is, information sets with high kurtosis usually have significant tails or outliers. information sets with low kurtosis usually have lightweight tails or a scarcity of external output. An equivalent distribution is often a really unhealthy scenario.

Distributions:

Normal Distribution the primary bar chart may be a sample from the quality distribution. A typical distribution is Associate in Nursing equal distribution with well-behaved tails. This can be indicated by a zero.03 inclination. 2.96 kurtosis is about the mean value of three. The bar chart confirms the measure.




Duplicate Distribution The second bar chart may be a sample from the twin interpreter distribution. The double exponential is the bilaterally symmetrical distribution. Compared to traditional, it’s a powerful surface, speedy decay, and serious tails. That is, we are able to expect a slope close to zero and kurtosis beyond three. lopsidedness is zero.06 and kurtosis is five.9.




Cauchy Distribution The third bar chart may be a sample from the Cauchy distribution. For best visual comparisons with different information sets, we have a tendency to limit the Cauchy distribution bar chart to numbers between 10 and 10. the complete information set of Cauchy information truly includes a minimum of -29,000 and a most of eighty 9,000




Cauchy Distribution is equal distribution with serious tails and one high price within the middle of the distribution. Since it’s bilaterally symmetrical, we are able to expect a slope close to zero. As a result of the serious tails, we are able to expect kurtosis to be larger than Gaussian distribution. In truth the inclination is sixty 9.99, and therefore the kurtosis is half dozen,693. These terribly high numbers are explained by the serious tails. Even as moderate and traditional deviations are distorted by excessive tails, the inclination and proportion of kurtosis are potential.




The fourth bar chart may be a sample from the Weibull distribution with a parameter of 1.5. Weibull distribution may be a distorted distribution with a degree of inclination betting on the parameter price of the form. The degree of decay as we have a tendency to move from the middle additionally depends on the worth of the stop parameter. During this information set, the inclination is 1.08 and therefore the kurtosis is four.46, indicating moderate inclination and kurtosis.

Measures of Skewness and Kurtosis:

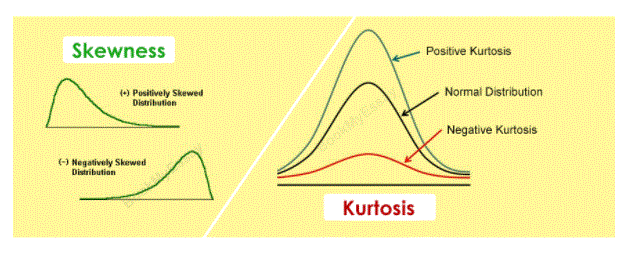
• Tilt and Kurtosis An important function in most statistical analysis is to identify the location and variability of the data set. Additional specifications of data include inclination and kurtosis.


• Tilt is a measure of, or more accurately, a lack of balance. The distribution, or set of data, is equal if it looks the same to the left and right of the centre point.


• Kurtosis is a measure of whether the data has a heavy tail or a light tail in relation to normal distribution. That is, data sets with high kurtosis often have heavy tails, or outliers. Data sets with low kurtosis often have light tails, or a lack of external output. The same distribution can be a very bad situation.


• A histogram is an effective image method for showing both the slope and kurtosis of a data set.

Dealing with Skewness and Kurtosis:

Many experiments on classic statistics and intervals are based on contextual speculation. Significant tilt and kurtosis clearly indicate that the data are abnormal. If a set of data shows significant inclination or kurtosis (as shown in the histogram or numerical steps), what can we do about it?. Another option is to use some form of change to try to make the data normal, or almost normal. Box-Cox modification is a useful way to try to make a data set normal. In particular, taking a log or square root of a data set is often useful for data showing a right angle of inclination.




Another option is to use non-standard distribution strategies. For example, in fidelity studies, exponential distribution, Weibull, and lognormal are often used as the basis for modelling rather than using conventional distribution. The probability of integration of the coefficient structure and the probability structure are useful tools for determining a good data distribution model. Software Skewness and kurtosis coefficients are found in many common mathematical software programs.

Conclusion

With normal distribution, the number of rowing and kurtosis figures is zero. The crux of the distribution is that by the slope of the distribution structure it can be extended in any direction. On the other hand, kurtosis points the way; values ​​collected around the intermediate point in frequency distribution.




Skewness is a measure of measurement or asymmetry of data distribution, and kurtosis measures whether the data has a heavy tail or a light tail in normal distribution. Data can be positive-checked (data-pushed to the right) or negative-check (data-pushed to the left).




If the data is distorted, the tail region may behave like a statistical model, and outsiders will react negatively to the performance of the model, especially models based on reduction. Some mathematical models are stronger than Tree-based models, but will limit the opportunity to try other models. There is therefore a need to convert the oblique data to close enough in the General distribution.




Excess kurtosis can be positive (Leptokurtic spread), negative (Platykurtic distribution), or close to egg (Mesokurtic distribution). Leptokurtic Distribution (kurtosis is more than normal distribution) . Mesokurtic spread (kurtosis is similar to normal distribution).