Dispersion in Statistics – Comprehensive Guide
Last updated on 08th Dec 2021, Blog, General
(5.0) | 18928 Ratings
987
Measures of dispersion describe the spread of the data. They include the range, interquartile range, standard deviation and variance. The range is given as the smallest and largest observations. This is the simplest measure of variability.
- Introduction of Measures of dispersion
- Dispersion in statistics
- Dispersion Measurement Characteristics
- Types of Dispersion Measures
- Benefits of Dispersion
- Conclusion
- This formulation is a definitional one and for calculations, an less complicated formulation is used. The computational formulation additionally avoids the rounding mistakes at some point of calculation.
- In each those formulation n – 1 is used in place of n withinside the denominator, as this produces a extra correct estimate of populace SD.
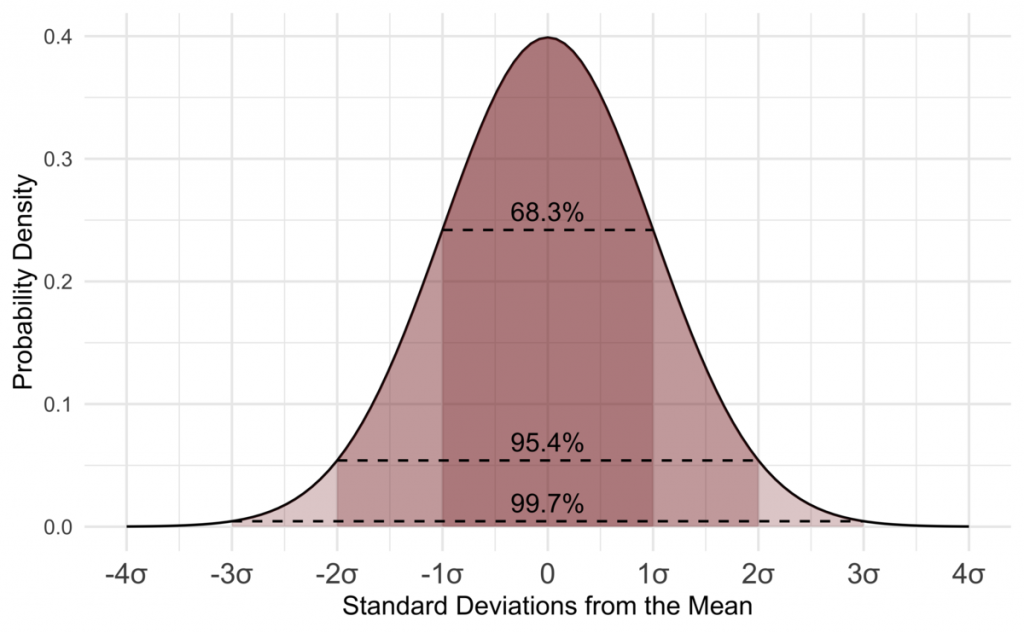
- The purpose why SD is a completely beneficial degree of dispersion is that, if the observations are from a ordinary distribution, then[3] 68% of observations lie among suggest ± 1 SD 95% of observations lie among suggest ± 2 SD and 99.7% of observations lie among suggest ± three SD.
- The different gain of SD is that along side suggest it could be used to hit upon skewness. The downside of SD is that it’s far an irrelevant degree of dispersion for skewed statistics.
- R= L – S
- Where R= vary, L= biggest price, S=smallest price
- Quartile deviation: this is often a degree of dispersion. during this technique, the excellence among the upper score and reduce score is taken and is thought because the interquartile selection. Symbolically it is as follows:
- Mean
- Where Q3= higher score Q1= Lower score
- It should be based on all of the observations in the data set.
- It should be based on all of the observations in the data set.
- It should be simple to understand and compute.
- It should be able to be further mathematically treated.
- It should be influenced by fluctuations in sampling.
- It should be influenced by extreme observations.
- Absolute Dispersion Measurement
- Dispersion Measurement Relative
- Range\sVariance
- Typical Deviation
- Quartiles and Deviation from the Quartile
- Mean and Standard Deviation
- Dispersion Measurement Relative
- Range Coefficient
- Variation Coefficient
- Standard Deviation Coefficient
- Quartile Deviation Coefficient
- Mean Deviation Coefficient
- They represent the dispersion of a statistical series.
- They are referring to the dependability or dependability of a series’ average value.
- They allow statisticians to compare the characteristics of two or more statistical series in terms of stability or consistency.
- They aid in controlling the variability of a phenomenon under his jurisdiction.
- They facilitate further statistical analysis of the series using devices such as co-efficient of skewness, co-efficient of correlation, variance analysis, and so on.
- They supplement central tendency measures in eliciting more and more information about the nature of a series.
Introduction:
The measures of primary tendency aren’t good enough to explain statistics. Two statistics units will have the identical suggest however they may be totally different. Thus to explain statistics, one desires to understand the quantity of variability. This is given with the aid of using the measures of dispersion. Range, interquartile variety, and general deviation are the 3 generally used measures of dispersion.
Range
The variety is the distinction among the biggest and the smallest statement withinside the statistics. The top gain of this degree of dispersion is that it is simple to calculate. On the alternative hand, it has lot of disadvantages. It could be very touchy to outliers and does now no longer use all of the observations in a statistics set.[1] It is extra informative to offer the minimal and the most values as opposed to imparting the variety.
Interquartile Range
Interquartile variety is described because the distinction among the twenty fifth and seventy fifth percentile (additionally referred to as the primary and 1/3 quartile). Hence the interquartile variety describes the center 50% of observations. If the interquartile variety is huge it method that the center 50% of observations are spaced huge apart. The essential gain of interquartile variety is that it could be used as a degree of variability if the intense values aren’t being recorded exactly (as in case of open-ended elegance periods with inside the frequency distribution).Other positive function is that it isn’t always suffering from intense values. The fundamental downside in the usage of interquartile variety as a degree of dispersion is that it isn’t always amenable to mathematical manipulation.
Standard Deviation
Standard deviation (SD) is the maximum generally used degree of dispersion. It is a degree of unfold of statistics approximately the suggest. SD is the rectangular root of sum of squared deviation from the suggest divided with the aid of using the quantity of observations.
Dispersion in statistics:
In statistics, the degree of vital tendency offers a divorced price that represents the complete cost; but, the vital tendency cannot describe the statement totally. The degree of dispersion permits U.S.A. to watch the variability of the objects. in an exceedingly applied mathematics sense, dispersion has meanings: initial it measures the variant of the objects amongst themselves, and 2nd, it measures the variant across the common. If the excellence among the price and customary is high, then dispersion could also be high. Otherwise it’ll doubtless be low. in line with Dr. Bowley, “dispersion is that the degree of the variant among objects.”
Researchers use this technique because it determines the responsibility of the common. Dispersion in addition permits a man of science in evaluating or larger series. it’s likewise the facilitating technique to several totally different applied mathematics ways like correlation, regression, structural equation modeling, etc. In statistics, dispersion has degree sorts. the primary is completely the degree, that measures the dispersion withinside the equal applied mathematics unit. The ordinal kind is that the relative degree of dispersion, that measures the quantitative relation unit. In statistics, there area unit varied ways which may be administrated to degree dispersion.
Range: vary is that the straightforward degree of dispersion, that’s delineate as a result of the excellence among the foremost vital price and also the smallest price. Mathematically, fully the and also the relative degree of selection could also be written because the subsequent:
Learn Advanced Python and Statistics for Financial Analysis Certification Training Course to Build Your Skills
Weekday / Weekend BatchesSee Batch DetailsMean Deviation: mean deviation from the mean could be a degree of dispersion, that’s referred to as the common deviation. mean deviation from the mean could also be computed from the imply or median. mean deviation from the mean is that the arithmetic deviation of assorted objects of vital tendency. It will be the imply or the median. Symbolically, imply deviation is delineate because the subsequent:
Where M= median, = meanStandard Deviation: within the degree of dispersion, identical recent deviation technique is that the most generally used technique. In 1983, it became initial used by Karl Pearson. variance is likewise referred to as root imply rectangular deviation. Symbolically it is as follows:
Where
D=Deviation
W= widespread deviation N= general style of observations.Variance: Variance is each alternative degree of dispersion. The fundamental quantity variance became initial used in 1918, through R.A Fisher. Variance is named the oblong of identical recent deviation. Symbolically, variance could also be written because the subsequent:
Variance= (S.D)
2 =
If we tend to perceive widespread deviation, then we are going to reckon the variance through squaring it. If we have variance, then we tend to can also reckon identical recent deviation, through the usage of the next formula:
Standard deviation encompasses a few mathematical properties. they’re as follows:1. variance of the n flavorer numbers could also be placed through the usage of the next formula:
Dispersion Measurement Characteristics:
The following characteristics define an ideal dispersion standard:
Types of Dispersion Measures:
Measures of dispersion in statistics aid in interpreting data variability, i.e. determining how homogeneous or heterogeneous the data is. In layman’s terms, it indicates how squeezed or scattered the variable is.
In statistics, there are two main types of dispersion methods:
Absolute Dispersion Measurement
When comparing the distributions of two or more data sets, relative measures of dispersion are used. This metric compares values without using units. Methods of relative dispersion that are commonly used include:
Benefits of Dispersion:
Conclusion:
In statistics, dispersion is a measure of the variability of data or terms. Such variability may result in random measurement errors if some of the instrumental measurements are found to be inaccurate. It is a statistical method of describing how the terms are distributed across different data sets.