An Introduction to Hidden Markov Models in Machine Learning

Introduction to Hidden Markov Models (HMM)

Hidden Markov Models (HMMs) are powerful statistical tools used for modeling sequences of observable events that are influenced by internal factors which are not directly observable. These hidden factors follow a Markov process, meaning the future state depends only on the current state and not on the sequence of events that preceded it. HMMs have been widely applied in fields such as speech recognition, natural language processing (NLP), bioinformatics, and time series analysis. They are particularly useful when the system being modeled has unobservable states but produces observable outputs influenced by these states.Hidden Markov Models (HMMs) are statistical models used to represent systems that are assumed to follow a Markov process with hidden (unobserved) states. In Machine Learning Training , an HMM is particularly useful when the system being modeled has observable outputs that depend on internal factors we cannot directly see. In essence, Baum-Welch Training Algorithm HMMs provide a way to model sequential data by combining probabilities of transitions between hidden states with the likelihood of observed outputs from those states. An HMM consists of a finite set of hidden states, transition probabilities between these states, and emission probabilities that link each hidden state to possible observations. The model assumes the Markov property, meaning that the future state depends only on the current state and not on the sequence of events that preceded it. Despite the simplicity of this assumption, HMMs are incredibly powerful. HMMs are widely used in various machine learning and signal processing applications, such as speech recognition, natural language processing, bioinformatics, and financial modeling. Key problems solved using HMMs include decoding the most likely sequence of hidden states (using the Viterbi algorithm), evaluating the probability of an observed sequence, and learning model parameters from data. HMMs remain a foundational tool for modeling time-series and sequential data.

Ready to Get Certified in Machine Learning? Explore the Program Now Machine Learning Online Training Offered By ACTE Right Now!

Components of HMM

An HMM is defined by the following components:

• States (S): The finite set of hidden states.
• Observations (O): The set of observed events.
• Transition Probabilities (A): The probability of moving from one state to another.
• Emission Probabilities (B): The probability of observing a symbol given a state.
• Initial Probabilities (π): The probability distribution over initial states.

These parameters together define the stochastic process that generates the observation sequences An Overview of ML on AWS .

Subscribe To Contact Course Advisor

Subscribe

Markov Chains vs HMM

Markov Chains are simpler models where the system is fully observable. The next state depends only on the current state, and both are known. In contrast, Machine Learning Training, HMMs introduce a level of complexity by assuming that the system has hidden states, which influence the observable outputs but are not directly accessible. You only observe emissions (outputs), not the states themselves. Therefore, you must infer the state sequence based on the observed data.

Feature	Markov Chain	Hidden Markov Model
Observability	Fully observable	Hidden states
Outputs	States themselves	Probabilistic emissions
Applications	Simple systems	Complex sequence modeling

To Explore Machine Learning in Depth, Check Out Our Comprehensive Machine Learning Online Training To Gain Insights From Our Experts!

Transition and Emission Probabilities

Transition probabilities define the likelihood of moving from one state to another. If there are N states, the transition matrix A is of size NxN, where A[i][j] is the probability of transitioning from state i to state j.Emission probabilities define how likely an observation is from a given state Keras vs TensorFlow . If there are M possible observations, the emission matrix B is NxM, where B[i][k] is the probability of observing symbol k from state i.

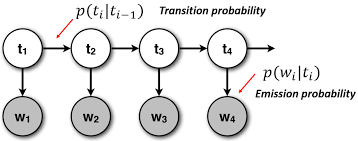
probabilities are crucial for sequence analysis, as they define the likelihood of any given sequence under the model.In a Hidden Markov Model (HMM), transition probabilities define the likelihood of moving from one hidden state to another. These are captured in a matrix where each entry represents the probability of transitioning from one state to the next, assuming the Markov property meaning the next state depends only on the current state, not the full history. On the other hand, natural language emission probabilities represent the likelihood of an observed output being generated from a particular hidden state. Since the states in an HMM are not directly observable, the emission probabilities allow us to relate the hidden process to real, observable data. Together, these two sets of probabilities enable the model to capture the structure of sequential data and make inferences about hidden patterns based on observed sequences. They are essential in applications like speech recognition, part-of-speech tagging, and biological sequence analysis.

Develop Your Skills with Machine Learning Training

Weekday / Weekend BatchesSee Batch Details

Forward and Backward Algorithms

Forward Algorithm

• Used to compute the probability of an observed sequence given an HMM.
• Employs dynamic programming to avoid redundant calculations.
• Calculates the total probability by summing over all possible hidden state sequences.
• Operates from the start of the sequence to the end.
• Efficient alternative to brute-force enumeration of all state paths.

Backward Algorithm

• Also computes the probability of an observed sequence, but in reverse.
• Works from the end of the sequence back to the start.
• Helps in tasks like parameter estimation during training (e.g., in the Baum-Welch algorithm).
• Often used in conjunction with the Cyber Extortion forward algorithm for posterior state estimation.

Looking to Master Machine Learning? Discover the Machine Learning Expert Masters Program Training Course Available at ACTE Now!

Viterbi Algorithm

The Viterbi algorithm is a dynamic natural language programming technique used to find the most probable sequence of hidden states (the Viterbi path) that leads to an observed sequence.The Viterbi Algorithm is a dynamic programming technique used in Hidden Markov Models (HMMs) to determine the most likely sequence of hidden states that could have generated a given sequence of observations. Machine Learning Engineer Salary Unlike the forward algorithm, which calculates the total probability of an observed sequence, the Viterbi algorithm focuses on finding the single most probable path through the state space. 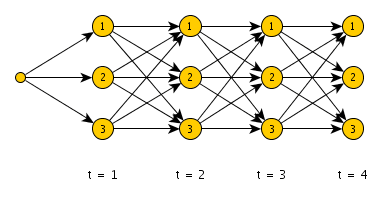It does this by recursively computing the maximum probability for each state at every time step, Forward and Backward Algorithms based on the most likely previous state and the emission and transition probabilities. The algorithm maintains a backpointer to trace the optimal path once the final state is reached. This makes the Viterbi algorithm essential in applications like speech recognition, part-of-speech tagging, bioinformatics, and error correction in communication systems, where identifying the most likely hidden sequence is critical.

Machine Learning Sample Resumes! Download & Edit, Get Noticed by Top Employers! Download

Baum-Welch Training Algorithm

The Baum-Welch Training algorithm is a special case of the Expectation-Maximization (EM) algorithm used to train HMMs.

It works iteratively:

• Expectation (E) Step: Use the forward and backward algorithms to estimate expected counts.
• Maximization (M) Step: Update the transition and emission probabilities based on these expectations.

This process is repeated until convergence. It allows the model to learn from unlabeled data, Best Machine Learning Tools which is particularly useful when manually annotating sequences is impractical.

Preparing for Machine Learning Job Interviews? Have a Look at Our Blog on Machine Learning Interview Questions and Answers To Ace Your Interview!

Applications in NLP and Bioinformatics

HMMs have broad applications:

NLP:
• Part-of-Speech Tagging: Assigning syntactic categories to words.
• Named Entity Recognition (NER): Identifying entities in text.
• Speech Recognition: Mapping audio signals to phonemes.

Bioinformatics:
• Gene Prediction: Identifying gene regions in DNA sequences.
• Protein Structure Prediction: Modeling protein sequences.
• Sequence Alignment: Comparing DNA or protein sequences.

Conclusion

Hidden Markov Models remain a fundamental concept in sequential data modeling. They balance mathematical elegance with practical utility in domains like NLP and bioinformatics. While newer models like RNNs and Transformers have gained popularity for their superior performance, In Machine Learning Training , the Baum-Welch training algorithm enhances the effectiveness of HMMs by estimating model parameters using the Forward and Backward Algorithms. Despite the rise of deep learning, HMMs still offer valuable insights, especially in data scarce and interpretable modeling environments, where understanding the underlying structure is just as important as prediction accuracy. Understanding HMMs equips learners and professionals with a robust statistical foundation for tackling natural language real-world sequence problems and forms a stepping stone toward mastering more advanced models.