Last updated on 07th Aug 2025| 10767
(5.0) |47257 Ratings
E-mail this post
- Introduction to Bias and Variance
- High Bias vs High Variance
- Underfitting and Overfitting
- Bias-Variance Decomposition
- Impact on Model Accuracy
- Visualization of the Tradeoff
- Regularization to Control Variance
- Cross-validation Techniques
- Conclusion
Introduction to Bias and Variance
In the field of machine learning, understanding the concepts of Bias-Variance Tradeoff is critical to building effective models. These two components contribute to the total prediction error and influence how well a model generalizes to unseen data. The tradeoff between bias and variance is central to the process of model selection, training, and evaluation. A well-balanced model must strike the right equilibrium between the two to achieve optimal performance. Bias refers to the error due to overly simplistic assumptions in the Machine Learning Training algorithm. High bias can cause a model to miss relevant relations between features and target outputs, leading to underfitting. Variance, Bias-Variance Decomposition Cross-validation on the other hand, refers to the error due to sensitivity to small fluctuations in the training set. High variance can cause a model to model the noise in the training data, leading to overfitting.
Ready to Get Certified in Machine Learning? Explore the Program Now Machine Learning Online Training Offered By ACTE Right Now!
High Bias vs High Variance
In machine learning, bias and variance are key sources of error that affect model performance and generalization.
- High Bias: occurs when a model makes strong assumptions about the data and oversimplifies the underlying patterns. This typically leads to underfitting, In Machine Learning Random Forest can help address situations where a model performs poorly on both the training and test data. Linear models applied to non-linear problems often suffer from high bias, which Random Forests are well-equipped to handle due to their ability to model complex, non-linear relationships.
- High Variance: on the other hand, happens when a model learns the training data too well, including its noise and fluctuations. This leads to overfitting, where the model performs well on the training data but poorly on new, unseen data. Complex models like deep neural networks are more prone to high variance when not properly regularized.
The ideal model strikes a balance between bias and variance this is known as the bias-variance tradeoff. Effective model tuning, feature selection, and regularization techniques help minimize both and improve generalization.
Underfitting and Overfitting
Underfitting occurs when a model is too simple to capture the underlying structure of the data. This is often the result of high bias and leads to poor performance on both the training and test data. Overfitting, on the other hand, happens when a model is excessively complex, capturing noise in the training data along with the underlying structure. Overfitting is a consequence of high variance and results in good Bias-Variance Decomposition performance but poor generalization.In machine learning, underfitting and overfitting are two common challenges that affect a model’s ability to generalize well to unseen data. Underfitting occurs when a model is too simple to capture the underlying patterns in the training data. This usually results from using an overly basic algorithm in Machine Learning Classification , Decomposition, insufficient training, or too few features. An underfitted model performs poorly on both the training set regularization to control variance and test set, indicating that it hasn’t learned enough from the data. For example, applying linear regression to a non-linear problem will likely lead to underfitting. On the other hand, overfitting happens when a model is too complex and learns not only the genuine patterns in the training data but also the random noise. This leads to excellent performance on the training data but poor generalization to new, unseen data. Overfitting is common in high-capacity models like deep neural networks when not properly regularized or trained on limited data. Achieving the right balance between underfitting and overfitting is critical for model success. Techniques such as cross-validation, regularization, pruning, and selecting the appropriate model complexity help mitigate these issues. The goal is to build a model that generalizes well, capturing essential patterns without being misled by noise.
To Explore Machine Learning in Depth, Check Out Our Comprehensive Machine Learning Online Training To Gain Insights From Our Experts!
Bias-Variance Decomposition
Total Error = Bias² + Variance + Irreducible Error
- Bias: Measures error due to overly simplistic assumptions in the model.High bias leads to underfitting.The model misses relevant patterns in the data.
- Variance: Measures error due to sensitivity to small fluctuations in the training data, which can be addressed differently in Keras vs TensorFlow High variance leads to overfitting.The model captures noise along with the signal.
- Tradeoff: Bias and variance are inversely related; reducing one often increases the other.The goal is to find a balance that minimizes total error on unseen data.
- Irreducible Error: Error caused by noise or randomness in the data itself.Cannot be eliminated regardless of the model.
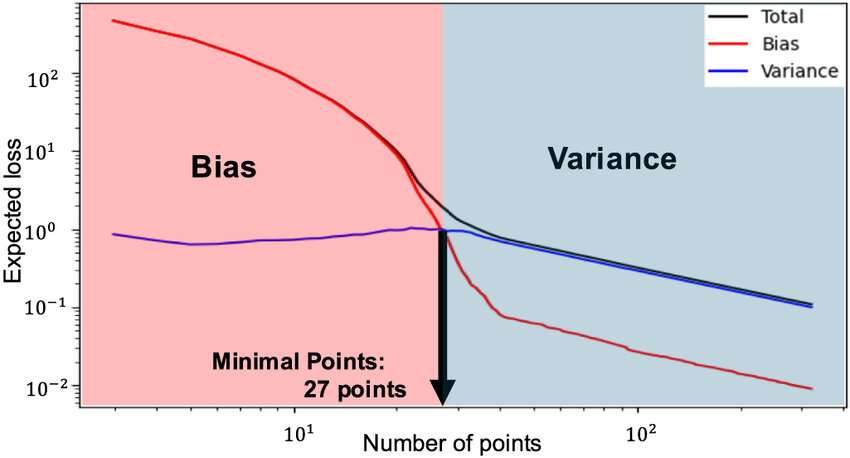
Impact on Model Accuracy
Bias-Variance Decomposition have a direct impact on model accuracy. High bias models underperform because they ignore the complexity of the data. High variance models might have high accuracy on the training set but perform poorly on new data. Achieving the right balance improves overall accuracy and model reliability.The balance between bias and variance plays a crucial role in determining a Machine Learning Training model’s accuracy. When a model has high bias, it oversimplifies the data, failing to capture important patterns, which leads to underfitting and poor accuracy on both training and test datasets. Conversely, a model with high variance is too sensitive to the training data, capturing noise along with the underlying patterns. This results in overfitting, where the model performs well on training data but poorly on unseen data, reducing its generalization ability. Achieving the right balance between bias and variance is essential to maximize accuracy. Models that effectively manage this tradeoff can generalize well, performing accurately on new, unseen data while maintaining good performance on training data. Techniques such as cross-validation, regularization, and careful model selection are employed to control bias and variance, ultimately improving the model’s predictive power and robustness.
Looking to Master Machine Learning? Discover the Machine Learning Expert Masters Program Training Course Available at ACTE Now!
Visualization of the Tradeoff
A common way to visualize the bias-variance tradeoff is through learning curves, which plot training and validation errors against model complexity or training set size. In such plots:High bias is indicated by both training and validation errors being high and close together.High variance is indicated by low training error but high validation error.
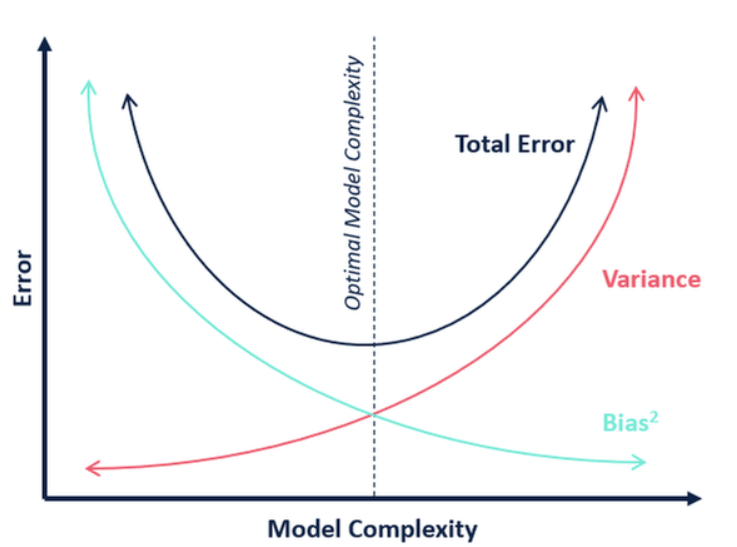
The balance between bias and variance has a direct impact on a machine learning model’s accuracy and generalization ability. A model with high bias tends to oversimplify the problem, leading to poor performance on both training and test data; this is known as underfitting. In contrast, A model with high variance may perform extremely well on training data but fail to generalize to unseen data due to overfitting, which can be mitigated using the Best Machine Learning Tools . This occurs when the model captures noise or random fluctuations instead of the true underlying patterns. The optimal model minimizes both bias and variance to achieve high accuracy on test data, not just training data. Understanding this trade-off allows practitioners to make informed choices about model complexity,Regularization to Control Variance training duration, Decomposition and regularization techniques. Properly managing bias and variance ensures the model remains robust and reliable in real-world applications, where unseen data is the norm. Visualizing these curves helps in diagnosing the source of poor model performance and selecting appropriate corrective measures.
Regularization to Control Variance
Regularization techniques like L1 (Lasso) and L2 (Ridge) regression help in reducing variance by penalizing large model coefficients. This prevents the model from fitting the noise in the training data.
- L1 Regularization (Lasso): Encourages sparsity by eliminating some weights completely.
- L2 Regularization (Ridge): Penalizes large weights and distributes weights more evenly.
Regularization introduces a bias but helps control overfitting, thus leading to better generalization.
Preparing for Machine Learning Job Interviews? Have a Look at Our Blog on Machine Learning Interview Questions and Answers To Ace Your Interview!
Cross-validation Techniques
Cross-validation helps in estimating model performance more reliably by training and testing the model on different data subsets. This technique helps identify whether a model suffers from high Bias-Variance Tradeoff in Tensorflow .
- K-Fold Cross Validation: Splits data into k subsets and rotates the training/testing process.
- Stratified K-Fold: Maintains class proportions across folds.
- Leave-One-Out Cross Validation (LOOCV): Uses a single observation as validation and the rest as training.
Cross-validation provides insights into model consistency and helps in hyperparameter Decomposition tuning machine learning to achieve the right balance between bias and variance.
Conclusion
The concepts of bias and variance are fundamental to understanding a machine learning model’s performance. High bias leads to underfitting, In Machine Learning Training , while high variance results in overfitting, both high bias and high variance reduce accuracy and generalization. Achieving the right balance between these two is crucial for building models that perform well on unseen data. that are both accurate and reliable. By applying proper techniques such as cross-validation, Regularization to Control Variance, and appropriate model selection, practitioners can reduce error and improve real-world performance. Ultimately, mastering the bias-variance trade-off is key to developing robust, high-performing machine learning systems.
