
- Introduction to Regularization
- Understanding Overfitting
- Ridge vs Linear Regression
- Cost Function of Ridge
- Role of Lambda (Regularization Strength)
- Mathematical Formulation
- Implementation in Python
- Use Cases
- Summary
Introduction to Regularization
In machine learning, the goal is to build models that generalize well on unseen data. However, complex models may memorize the training data instead of learning underlying patterns, a phenomenon known as overfitting. This is where regularization comes in. Regularization is a technique used to prevent overfitting by adding a penalty to the loss function. This discourages overly complex models by controlling the size of the model coefficients. It essentially trades a bit of training accuracy for better generalization.In this guide, we focus on Ridge Regression, which is a regularized form of linear regression and is extremely effective when dealing with multicollinearity or high-dimensional data.Regularization is a technique used in Machine Learning Training to prevent overfitting, which occurs when a model learns the training data too well, including its noise and outliers, Ridge vs Linear Regression and performs poorly on new, unseen data. By adding a penalty term to the model’s loss function, regularization discourages overly complex models and encourages simpler, more generalizable ones. The two most common types of regularization are L1 (Lasso) and L2 (Ridge). L1 regularization adds the absolute values of the model’s coefficients as a penalty, promoting sparsity by driving some coefficients to zero, effectively performing feature selection. L2 regularization adds the squared values of the coefficients, which shrinks them toward zero but rarely eliminates any completely. Regularization techniques are essential for improving a model’s ability to generalize beyond the training dataset, Cost Function leading to more robust and reliable predictions in real-world applications.
Ready to Get Certified in Machine Learning? Explore the Program Now Machine Learning Online Training Offered By ACTE Right Now!
Understanding Overfitting
Overfitting occurs when a model learns the noise in the training data rather than the actual pattern. It fits the training data too well, resulting in poor performance on test or real-world data.
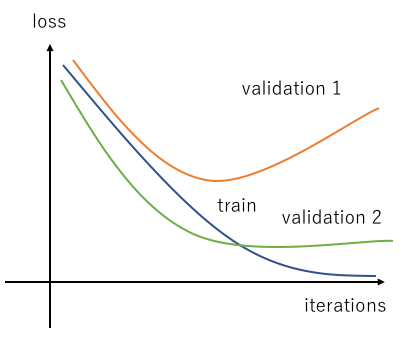
Symptoms of Overfitting:
- High accuracy on training data but low accuracy on test data.
- Complex decision boundaries.
- High variance and low bias.
Support Vector Machine Regularization techniques like Ridge Regression address overfitting by introducing a penalty term that controls the model complexity. By penalizing large weights, the model becomes smoother and more generalizable.Ridge Regression doesn’t completely eliminate features (like Lasso can) but shrinks the coefficients, Ridge vs Linear Regression making it especially useful in situations where all features are believed to be relevant but multicollinearity exists.
Ridge Regression vs Linear Regression
Linear Regression attempts to fit a linear relationship between features and the target variable by minimizing the Mean Squared Error (MSE). However, Decision Trees in Machine Learning When there are many features or multicollinearity, linear regression becomes unstable. Ridge Regression, on the other hand, modifies the cost function of linear regression by adding a regularization term (L2 penalty):
Linear Regression Cost Function:
J(θ)=12m∑i=1m(yi−y^i)2J(\theta) = \frac{1}{2m} \sum_{i=1}^m (y_i – \hat{y}_i)^2
Ridge Regression Cost Function:
J(θ)=12m∑i=1m(yi−y^i)2+λ∑j=1nθj2J(\theta) = \frac{1}{2m} \sum_{i=1}^m (y_i – \hat{y}_i)^2 + \lambda \sum_{j=1}^{n} \theta_j^2
Where:
- λ\lambda is the regularization parameter
- θj\theta_j are the model coefficients
- λ\lambda: Regularization strength
- θ\theta: Coefficients of the model
- Small λ → behaves like Linear Regression (less regularization).
- Large λ → heavily penalizes large coefficients (more regularization).
- λ = 0: No regularization, risk of overfitting.
- λ too large: Underfitting, as the model is overly constrained.
- XTXX^TX: Feature covariance matrix
- λI\lambda I: Regularization matrix (I = identity matrix)
- θ\theta: Vector of model parameters
- import numpy as np
- import pandas as pd
- from sklearn.linear_model import Ridge
- from sklearn.model_selection import train_test_split
- from sklearn.metrics import mean_squared_error
- from sklearn.datasets import load_diabetes
- X, y = load_diabetes(return_X_y=True)
- X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.2, random_state=42)
- ridge = Ridge(alpha=1.0)
- ridge.fit(X_train, y_train)
- y_pred = ridge.predict(X_test)
- print(“MSE:”, mean_squared_error(y_test, y_pred))
- print(“R^2 Score:”, ridge.score(X_test, y_test))
- print(“Coefficients:”, ridge.coef_)
- Marketing: Sales forecasting based on hundreds of features (ads, customer behavior).
- Sports Analytics: Performance prediction using multiple player stats.
- Text Analytics: Regression with high-dimensional TF-IDF features.
To Explore Machine Learning in Depth, Check Out Our Comprehensive Machine Learning Online Training To Gain Insights From Our Experts!
Cost Function of Ridge Regression
The cost function of Ridge Regression includes both the original loss and the regularization term.
J(θ)=MSE+λ∑j=1nθj2J(\theta) = \text{MSE} + \lambda \sum_{j=1}^{n} \theta_j^2<>/p>
Where:
MSE = Mean Squared Error: 12m∑i=1m(yi−Xi⋅θ)2\frac{1}{2m} \sum_{i=1}^{m} (y_i – X_i \cdot \theta)^2
The regularization term ensures that the weights do not become too large. While MSE focuses on fitting the data, Penalty term controls model complexity in Machine Learning Training. Minimizing this function balances the trade-off between fitting the training data and keeping the weights small.
Role of Lambda (Regularization Strength)
The λ (lambda) parameter in Ridge Regression controls the amount of shrinkage applied to the coefficients.
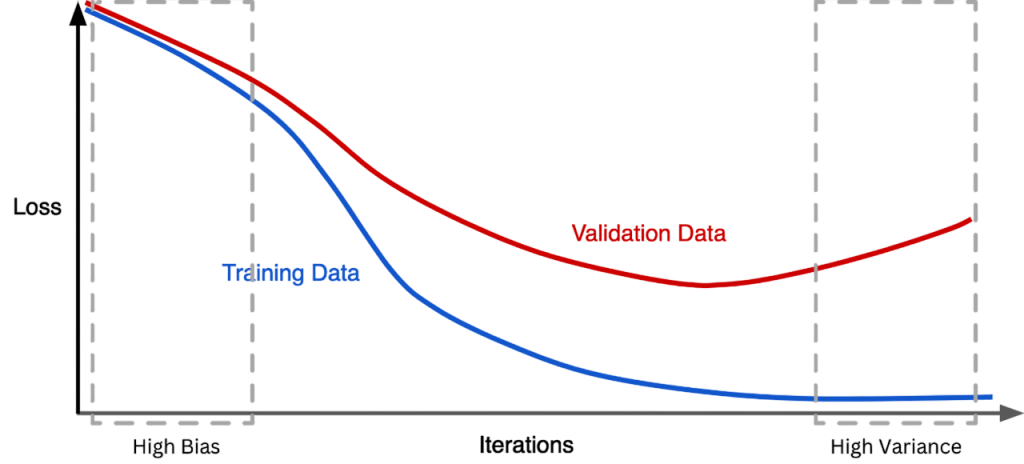
Visual Effect:
Choosing the right λ is critical. Pattern Recognition and Machine Learning This is often done using cross-validation, where the model is trained on different subsets of data and tested on others to find the λ that minimizes error.
Looking to Master Machine Learning? Discover the Machine Learning Expert Masters Program Training Course Available at ACTE Now!
Mathematical Formulation
Given a design matrix X∈Rm×nX \in \mathbb{R}^{m \times n} and response vector y∈Rmy \in \mathbb{R}^m, Ridge Regression solves:
θ=(XTX+λI)−1XTy\theta = (X^TX + \lambda I)^{-1}X^Ty
Where:This equation ensures the matrix is invertible, Deep Learning Explained which is especially helpful when features are correlated or when the number of features exceeds the number of samples.The closed-form solution makes Ridge Regression computationally efficient, Ridge vs linear regression even in high dimensions.
Implementation in Python
Here’s a basic implementation of Ridge Regression using scikit-learn:
Step 1: Import Libraries
Step 2: Load Data
Step 3: Train Ridge Model
Step 4: Evaluate Model
Step 5: Coefficient Analysis
By adjusting alpha, you can control the model’s complexity and generalization performance.
Preparing for Machine Learning Job Interviews? Have a Look at Our Blog on Machine Learning Interview Questions and Answers To Ace Your Interview!
Use Cases
Ridge Regression is widely used in scenarios Cost Function of Ridge where model interpretability Ridge vs Linear Regression and performance under multicollinearity are important. Common Use Cases: An Overview of ML on AWS Healthcare: Predicting patient outcomes from high-dimensional genomic data. Finance: Risk modeling where many correlated indicators exist.
Ridge Regression is particularly suited for continuous output prediction problems where all features carry potential predictive power.
Summary
Ridge Regression is a powerful tool that enhances linear regression by incorporating L2 regularization. It helps to control overfitting, manage multicollinearity, Cost Function of Ridge and improve model generalization.Ridge Regression is a powerful regularization technique that helps address overfitting in linear models by penalizing large coefficients through L2 regularization. By introducing a regularization parameter (lambda), it balances the trade-off between fitting the Machine Learning Training data well and maintaining model simplicity for better generalization. Unlike standard linear regression, Ridge Regression is particularly effective when dealing with multicollinearity or high-dimensional data. While it doesn’t eliminate features like Lasso, it ensures more stable and robust predictions. Overall, Ridge Regression is a valuable tool in any machine learning practitioner’s toolkit for building reliable, generalizable models.




