
- Introduction to Mathematics in Data Science
- Why Math is Important for Data Science
- Key Mathematical Concepts for Data Science
- Linear Algebra and its Role in Data Science
- Probability and Statistics for Data Analysis
- Calculus in Machine Learning Algorithms
- Optimization Techniques in Data Science
- Graph Theory and Network Analysis
- Real-World Applications of Math in Data Science
- Best Resources to Learn Math for Data Science
- Common Challenges in Learning Math for Data Science
- Future of Mathematical Applications in AI and Data Science
Interested in Obtaining Your Data Science Certificate? View The Data Science Course Training Offered By ACTE Right Now!
Introduction to Mathematics in Data Science
Mathematics is a foundational element of data science, providing the tools and techniques necessary for data analysis, modeling, and interpretation. Data science encompasses various activities, including machine learning, statistical analysis, data visualization, and predictive analytics, which rely heavily on mathematical concepts. A solid understanding of mathematics is essential for anyone pursuing a career in Data Science. It enables data scientists to formulate models, make data-driven decisions, and develop algorithms that extract meaningful insights from large datasets. This article will explore the importance of mathematics in data science, key mathematical concepts used in the field, and how these concepts are applied in real-world scenarios.

Why Math is Important for Data Science
Mathematics is integral to data science for several reasons:
- Data Modeling: Mathematical techniques help scientists create models representing real-world phenomena. This can range from linear regression models to complex deep-learning neural networks. These models require mathematical formulations to ensure their accuracy and effectiveness.
- Algorithm Development: Many machine learning algorithms, such as decision trees, support vector machines, and neural networks, rely on mathematical foundations. Understanding and improving algorithms requires knowledge of various mathematical principles.
- Quantitative Analysis: Data science deals with large datasets, and interpreting these datasets involves statistical and probabilistic reasoning. Without a strong mathematical background, data scientists would struggle to assess data distributions, correlations, and variances, or to make valid predictions.
- Optimization: Optimization problems are prevalent in data science, whether it’s minimizing the error in a predictive model or finding the best parameters for machine learning algorithms. Mathematics, particularly calculus and linear algebra, is crucial in identifying optimal solutions.
- Reproducibility and Validation: Mathematical reasoning ensures the reproducibility of data analysis and the validation of models. This is important for ensuring that the insights gained are reliable and can be generalized to unseen data.
Key Mathematical Concepts for Data Science
Several branches of mathematics are fundamental to data science. Key areas include:- Linear Algebra: This branch focuses on vector spaces and linear mappings between them. It is central to many data science applications, especially in machine learning algorithms and the manipulation of large datasets. Linear algebra concepts such as matrices, eigenvalues, and eigenvectors are essential for operations like dimensionality reduction and matrix factorization.
- Probability and Statistics: These two fields allow data scientists to quantify uncertainty, make inferences, and draw conclusions from data. Probability helps in understanding data distributions, while statistics is essential for hypothesis testing, estimation, and statistical modeling.
- Calculus plays a key role in many areas of data analysis and machine learning, especially when exploring topics like Big Data vs Data Science. It involves the study of change, using concepts such as derivatives, integrals, and gradient descent to optimize models and enhance their performance.
- Optimization: Optimization techniques are used to improve the performance of models by minimizing or maximizing certain functions (like cost functions). Techniques such as gradient descent are used in many machine learning algorithms.
- Graph Theory and Network Analysis: In scenarios where data is represented as a graph (nodes and edges), understanding graph theory becomes important. Network analysis, social network analysis, and recommendation systems all rely on graph theory to model relationships between entities.
Linear Algebra and its Role in Data Science
Linear algebra is a central concept in data science, especially in areas like machine learning, computer vision, and natural language processing. The following are some key uses of linear algebra in data science:
- Data Representation: Data is often represented as matrices or vectors in data science. For example, a dataset with multiple features can be represented as a matrix, where each row corresponds to an observation and each column to a feature.
- Dimensionality Reduction: Techniques like Principal Component Analysis (PCA) use linear algebra to reduce the number of variables in a dataset while preserving its essential structure. PCA works by identifying the eigenvectors of the data matrix and projecting data onto lower-dimensional spaces.
- Solving Systems of Equations: Linear algebra helps solve systems of equations, which are often encountered when solving optimization problems in machine learning algorithms like linear regression or neural networks.
- Eigenvalues and Eigenvectors: Eigenvalues and eigenvectors are used in many machine learning techniques, including dimensionality reduction and clustering algorithms such as spectral clustering.
Probability and Statistics for Data Analysis
Frequency Range
Probability and statistics are critical for understanding the data and drawing meaningful insights from it. These two branches of mathematics enable data scientists to quantify uncertainty and make predictions based on data. Key concepts include:
- Descriptive Statistics: Descriptive statistics help summarize and describe the main features of a dataset, such as measures of central tendency (mean, median) and variability (variance, standard deviation).
- Inferential Statistics: Inferential statistics involves making predictions or generalizations about a population based on a sample. Techniques like hypothesis testing, confidence intervals, and p-values allow data scientists to draw conclusions about data with a certain degree of confidence.
- Probability Distributions: Concepts like probability distributions are fundamental in data science, where models often rely on distributions such as normal, binomial, and Poisson to represent data. These distributions help describe the likelihood of different outcomes and are used in tasks like classification, regression, and Bayesian inference. To dive deeper into these topics, consider exploring this Data Science Training program.
- Bayesian Inference: Bayesian statistics provides a framework for updating the probability of a hypothesis based on new evidence. This approach is used in machine learning models like Bayesian networks and Naive Bayes classifiers.
Calculus in Machine Learning Algorithms
Calculus plays a vital role in the development and optimization of machine learning algorithms. The following are a few key ways calculus is applied:
- Optimization: Many machine learning models require optimization techniques to find the best parameters. Calculus, especially derivatives and partial derivatives, is used to find the local minima or maxima of functions. The most commonly used optimization technique in machine learning is gradient descent, which relies on the derivative to update a model’s parameters.
- Cost Function: In machine learning, the cost function (also known as the loss function) measures how well a model performs by comparing its predictions to actual outcomes. Calculus is crucial in minimizing this cost function by adjusting the model’s parameters using methods like gradient descent. For those interested in mastering these concepts, Data Science Training can provide you with the knowledge and skills needed..
- Backpropagation: In neural networks, backpropagation adjusts weights based on the error produced during prediction. Calculus (specifically the chain rule) propagates errors backward through the network and adjusts weights accordingly.
- Continuous Change: Calculus allows data scientists to model continuous change in data. For instance, when predicting trends or performing time series analysis, calculus helps model the rate of change over time.
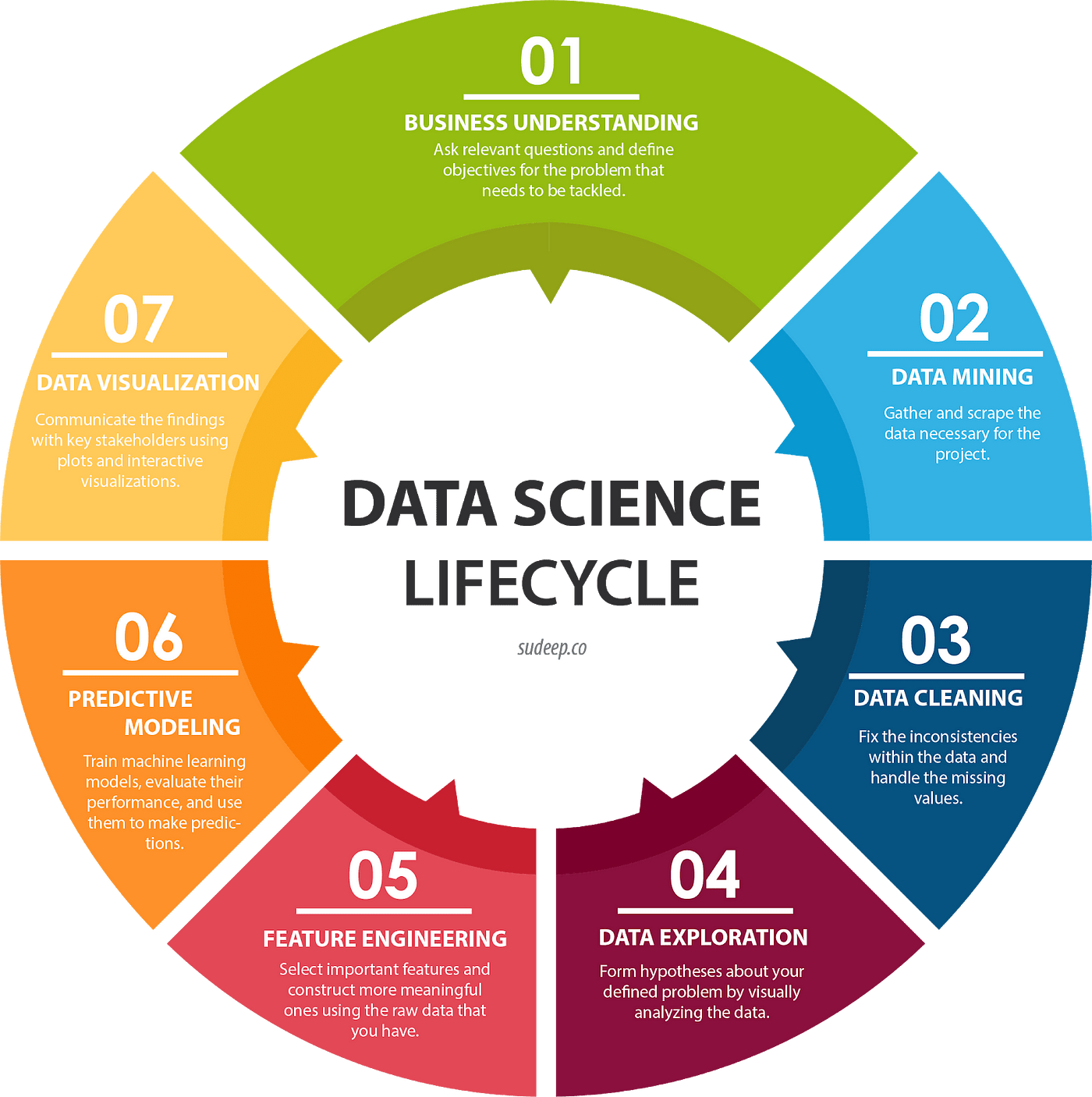
Optimization Techniques in Data Science
Optimization techniques are crucial for improving the performance of machine learning algorithms. Optimization involves minimizing or maximizing certain functions, such as cost or objective functions. Some standard optimization techniques in data science include:
- Gradient Descent: Gradient descent is an iterative optimization algorithm that minimizes the cost function by adjusting model parameters in the opposite direction of the gradient.
- Stochastic Gradient Descent (SGD): A variant of gradient descent where the model parameters are updated after each data point rather than the entire dataset. This method is commonly used for large datasets and online learning.
- Linear Programming: Linear programming involves solving optimization problems with linear objective functions and constraints. It is used in various applications such as resource allocation and supply chain optimization.
- Convex Optimization: Convex optimization is concerned with minimizing convex functions, which are used in machine learning models like support vector machines and logistic regression.
Graph Theory and Network Analysis
- Social Network Analysis: Graph theory is used to model relationships between individuals or entities in social networks. It helps in analyzing the spread of information, communities, and centrality measures (e.g., PageRank in Google search algorithms).
- Recommendation Systems: Graphs can represent products and users in recommendation systems. Collaborative filtering algorithms often use graph-based models to predict user preferences.
- Network Connectivity: Graph theory helps analyze the connectivity and flow of information in networks such as computer networks, communication systems, or transport networks.
- Predictive Modeling: In finance, math is used to build predictive models for stock market trends, credit scoring, and fraud detection.
- Image Processing: In computer vision, linear algebra, and calculus are used for image recognition, object detection, and feature extraction.
- Healthcare: Mathematical models help in disease prediction, medical image analysis, and personalized treatment recommendations.
- Marketing: Analytics and probability theory are used for customer segmentation, campaign optimization, and churn prediction.
- Online Courses: Websites like Coursera, edX, and Udacity offer courses in topics like linear algebra, probability, and calculus with a focus on data science applications.
- Books: Mathematics for Machine Learning” by Marc Peter Deisenroth, A. Aldo Faisal, and Cheng Soon Ong is an excellent resource for understanding the mathematics behind data science.
- Khan Academy: This free platform provides excellent resources for learning foundational mathematics such as algebra, probability, and calculus.
- Abstract Concepts: Some mathematical concepts, like linear algebra or probability theory, seem abstract and hard to relate to practical applications.
- Mathematical Rigor:Understanding the rigorous proofs and derivations behind algorithms and models can be challenging for some learners.
- Interdisciplinary Nature:Data science combines mathematical knowledge with computer science and domain expertise, which can be overwhelming.
Graph theory is key in analyzing complex systems where data is represented as networks or graphs. In data science, graph theory is applied in several areas:
Go Through These Data Science Interview Questions and Answers to Excel in Your Upcoming Interview.
Real-World Applications of Math in Data Science
Mathematics is applied in numerous real-world scenarios in data science, including:
Best Resources to Learn Math for Data Science
Many resources are available to help you strengthen your math skills for data science. Some popular options include:
Common Challenges in Learning Math for Data Science
While mathematics is critical for data science, many learners struggle to master mathematical concepts. Common challenges include:
Future of Mathematical Applications in AI and Data Science
As AI and data science continue to evolve, mathematics’s role will only become more crucial. Future advancements in machine learning, deep learning, and AI are likely to rely heavily on new mathematical techniques, especially in areas such as optimization, probabilistic modeling, and algorithm development. Mathematics will continue to shape the future of AI, ensuring that data scientists are equipped to tackle increasingly complex challenges and unlock new insights from data.




